Question
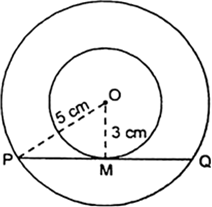
दो सकेंद्रीय वृत्तों की त्रिज्याएँ 5cm तथा 3cm हैं। बड़े वृत्त की उस जीवा की लंबाई ज्ञात कीजिए जो छोटे वृत्त को स्पर्श करती हो।
Solution
माना, दिए गए दो सकेंद्रीय वृत्तों का केंद्र O है तथा PQ बड़े वृत्त की जीवा है जो छोटे वृत्त को बिंदु M पर स्पर्श करती है।
OP तथा OM को मिलाओ।
हम जानते हैं कि स्पर्श रेखा और त्रिज्या परस्पर लम्बवत्त होती है।
∴ 
अब, समकोण ΔOMP में,
OP2 = OM2 + PM2
[पाइथागोरस प्रमेय के प्रयोग से]
⇒ (5)2 = (3)2 + PM2
⇒ 25 = 9 + PM2
⇒ PM2 = 16
⇒ PM = 4 cm
PM = MQ = 4 cm
∴ PQ = 2 PM = 2 x 4 = 8 cm
अत: जीवा AB की लंबाई = 8 cm
