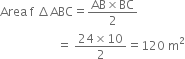Mathematics Chapter 14 Statistics
Sponsor Area
NCERT Solution For Class 9 About 2.html
A traffic signal board, indicating ‘SCHOOL AHEAD’, is an equilateral triangle with side ‘a’. Find the area of the signal board, using Heron’s formula. If its perimeter is 180 cm, what will be the area of the signal board?
'a' = a
'b' = a
'c' = a![]()
Area of the signal board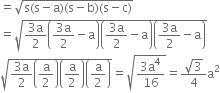
Perimeter = 180 cm![]() 'a' + 'b' + 'c' = 180
'a' + 'b' + 'c' = 180![]() a + a + a = 180
a + a + a = 180![]() 3a = 180
3a = 180![]()
![]() a = 60 cm
a = 60 cm![]() Area of the signal board
Area of the signal board ![]()
![]()
Alternatively,
![]()
Area of the signal board
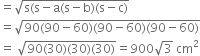
The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 122 m, 22 m and 120 m (see figure). The advertisements yield an earning of र5000 per m2 per year. A company hired one of its walls for 3 months. How much rent did it pay?
a =122 m
b = 22 m
c = 120 m
1 year =12 months
V Rent for 12 months per m2= र 5000
![]() Rent for 1 month per m2 = र
Rent for 1 month per m2 = र![]()
![]() Rent for 3 months of 1320 m2
Rent for 3 months of 1320 m2
![]()
![]() Rent for 3 months of 1320 m2
Rent for 3 months of 1320 m2
= र (1250 x 1320)
= र 1650000.
There is a slide in a park. One of its side walls has been painted in some colour with a message “KEEP THE PARK GREEN AND CLEAN”. If the sides of the wall are 15 m, 11 m and 6 m, find the area painted in colour.
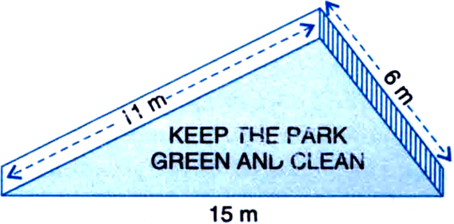
a = 15 m
b = 11 m
c = 6 m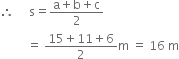
![]() Area painted in colour
Area painted in colour
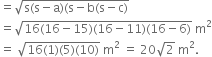
Find the area of a triangle two sides of which are 18 cm and 10 cm and the perimeter is 42 cm.
a = 18 cm
b = 10 cm Perimeter - 42 cm
⇒ a + b + c = 42
⇒ 18 + 10 + c = 42
⇒ 28 + c = 42
⇒ c = 42 – 28
⇒ c = 14 cm
![]()
![]() Area of the triangle
Area of the triangle
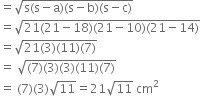
Sides of a triangle are in the ratio of 12 :17 : 25 and its perimeter is 540 cm. Find its area.
Let the sides of the triangle be 12k, 17k and 25 k cm.
Then,
Perimeter = 12k+ 17k + 25k = 54k
According to the question,
54k = 540![]()
![]() k = 10
k = 10![]() a = 12k = 12 x 10 = 120 cm
a = 12k = 12 x 10 = 120 cm
b = 17k = 17 x 10 = 170 cm
c = 25k = 25 x 10 = 250 cm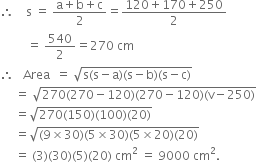
An isosceles triangle has perimeter 30 cm and each of the equal sides is 12 cm. Find the area of the triangle.
a = 12 cm
b = 12 cm
Perimeter = 30 cm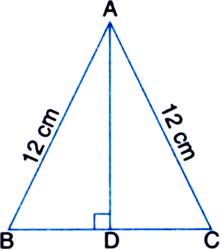
⇒ a + b + c = 30
⇒ 12 + 12 + c = 30
⇒ 24 + c = 30
⇒ c = 30 – 24
⇒ c = 6 cm
![]()
![]() Area of the triangle
Area of the triangle
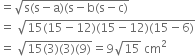
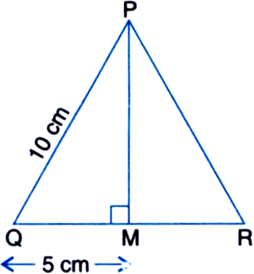
In the following figure, calculate the area of the shaded portion:
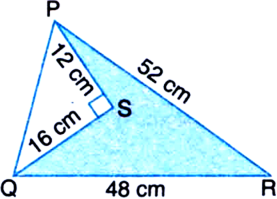
In right triangle PSQ,
PQ2 = PS2 + QS2
| By Pythagoras Theorem
= (12)2 + (16)2
= 144 + 256 = 400![]()
New, for ![]()
a = 20 cm
b = 48 cm
c = 52 cm 
∴ Area of the shaded portion
= Area of ΔPQR – Area of ΔPSQ
= 480 – 96 = 384 cm2.
Find the area of a right angled triangle if the radius of its circumcircle is 3 cm and altitude drawn to the hypotenuse is 2 cm.
Let ABC be the right angled triangle right angled at B. Let O be the centre of the circumcircle.
Then, O is the mid-point of the hypotenuse
AC. | by geometry
OA = OB = OC
= radius of the circumcircle = 3 cm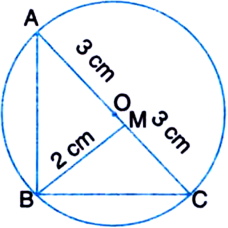
∴ Hypotenuse AC = Diameter of the circle
= 2 x radius of the circumcircle
= 2 x 3 = 6
cm Let BM be the perpendicular from B on AC.
∴ BM = 2 cm
∴ Area of the right angled triangle ABC
A regular hexagon has a side 8 cm. Determine its perimeter and area.
Side = 8 cm
∴ Perimeter = 6 x 8 = 48 cm
Area of equilateral triangle OAB![]()
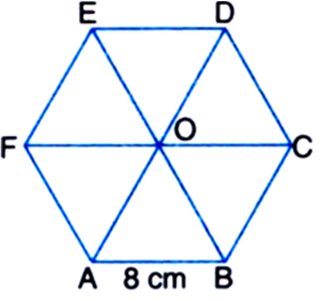
![]()
∴ Area of the regular hexagon
= 6 x Area of equilateral triangle OAB![]()
Sides of a triangle are in the ratio 13 : 14 : 15 and its perimeter is 84 cm. Find its area.
Let the sides of the triangle be 13k, 14k and 15k (in cm). Then,
perimeter = a + b + c
= 13k + 14k + 15k
= 42k cm
According to the questions,
42k = 84![]()
∴ Sides are 26 cm, 28 cm and 30 cm.
The base of an isosceles triangle measures 24 cm and its area is 60 cm2. Find its perimeter.
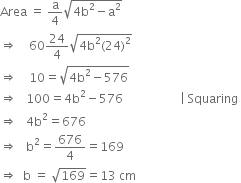
∴ Perimeter = a + b + b
= 24 + 13 + 13
= 50 cm
The unequal side of an isosceles A is 6 cm and its perimeter is 24 cm. Find its area.
b + b + 6 = 24![]() b = 9 cm
b = 9 cm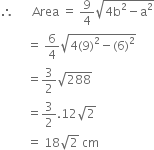
The sides of a triangular ground are 5 m, 7 m and 8 m respectively. Find the cost of levelling the ground at the rate of र 10 per m2. (Use  = 1.73).
= 1.73).
For triangular ground
a = 5 m
b = 7 m
c= 8 m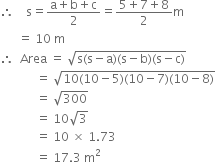
Cost of levelling
= 17.3 x 10 = र 173
An isosceles triangle has perimeter 30 m and each of the equal sides is 12 cm. Find area of the triangle.
Let the third side be x cm. Then,
12 + 12 + x = 30![]() 24 + x = 30
24 + x = 30![]() x = 6 cm
x = 6 cm
So, a = 12 cm
b = 12 cm
c = 6 cm![]()
The sides of a triangular park are in the ratio 3 : 5 : 7 and its perimeter 600 m. Find the area of the triangle.
Let the sides of the triangle be 3k, 5k and 7k (in m). Then,
a = 3k
b = 5k
c = 7k
∴ Perimeter = a + b + c
= 3k + 5k + 7k = 15k
According to the question,
15k = 600
⇒ k = 40
∴ a = 120 m
b = 200 m
c = 280 m![]()
![]() Area of the triangle
Area of the triangle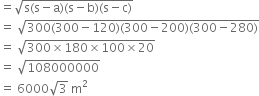
The perimeter of a right triangle is 24 cm. If its hypotenuse is 10 cm, find its area.
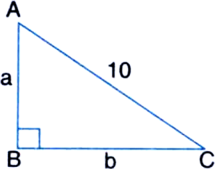
a + b + 10 = 24
⇒ a + b = 14 ...(1)
Also, a2 + b2 = (10)2
⇒ a2 + b2 = 100 ...(2)
We know that
(a + b)2 = a2 + b2 + 2ab
⇒ (14)2 = 100 + lab
⇒ 2ab = 96
⇒ ab = 48 ...(3)
Also, (a – b)2 = a2 + b2 – 2ab
= 100 – 2 x 48 = 100 – 9b
= 4 | if a > b
⇒ a – b = 2 ....(4)
Solving (1) and (4), we get a = 8 cm b = 6 cm![]()
The perimeter of a triangularfield is 300 cm and its sides are in the ratio 5 : 12 : 13. Find the length of the perpendicular from the opposite vertex to the side whose length is 130 cm.
∴ Area of the triangular field
Let the length of the perpendicular from the opposite vertex to the side whose length is 130 cm be h cm. Then,
Area of the triangular field
![]()
From (1) and (2),
65h = 3000![]()
Sponsor Area
The sides of a triangular park are 8 m, 10 m and 6 m respectively. A small circular area of diameter 2 m is to be left out and the remaining area is to be used for growing roses. How much area is used for growing roses? (Use π = 3.14).
For triangular park
∵ 62 + 82 = 102
∴ Angular between sides of length 6 m and
8 m = 90°
∴ Area of the triangular park![]()
Radius of circular area (r)![]()
∴ Circular area = ![]()
∴ Area used for growing uses
= Area of the triangular part
- Circular area
= 24 – 3.14 = 20.86 m2
Find the area of an isosceles triangle each of whose equal sides is 13 cm and whose base is 24 cm.
Here, a = 24 cm
b = 13 cm
The sides of a right triangle ABC are 5 cm, 12 cm and 13 cm. Find the area of the triangle.
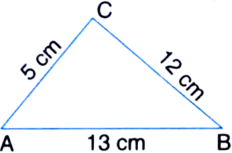
Solution not provided.
30 cm2
Find the area of an isosceles triangle with two equal sides as 5 cm each and unequal side as 8 cm.
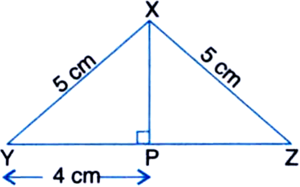
Solution not provided.
Ans. 12 cm2
Find the area of a triangle whose sides are 40 cm, 24 cm and 32 cm.
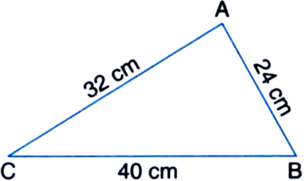
Solution not provided.
Ans. 384 cm2
Find the area of a triangle two sides of which are 8 cm and 11 cm and the perimeter is 32 cm.
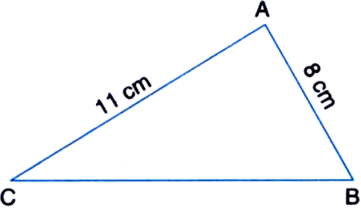
Solution not provided.
Ans. ![]()
The sides of a triangular plot are in the ratio 3 : 5 : 7 and its perimeter is 300 m. Find its area.
Solution not provided.
Ans. ![]()
Find the area of a triangle, two sides of which are 60 cm and 100 cm and the perimeter is 300 cm.
Solution not provided.
Ans. ![]()
Find the area of a triangle whose sides are 6.5 cm, 7 cm and 7.5 cm.
Solution not provided
Ans. 21 cm2
Find the area of the triangle whose two sides are of measure 13 cm and 14 cm and perimeter is 42 cm.
Solution not provided
Ans. 84 cm2
The perimeter of a triangular ground is 900 m and its sides are in the ratio 3 : 5 : 4. Using Heron’s formula, find the area of the ground.
Solution not provided
Ans. 337550 cm2
The unequal side of an isosceles triangle is 6 cm and its perimeter is 24 cm. Find its area.
Solution not provided
Ans. ![]()
Find the area of a triangle, whose sides are 26 cm, 28 cm and 30 cm respectively.
Solution not provided
Ans. 336 cm2
An isosceles triangle has perimeter 30 cm and each of the equal sides is 12 cm. Find the area of the triangle.
Solution not provided
Ans. ![]()
A park, in the shape of a quadrilateral ABCD, has ∠C = 90°, AB = 9 m, BC = 12 m, CD = 5 m and AD = 8 m. How much area does it occupy?
Join BD.
Area of right triangle BCD
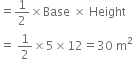
In right triangle BCD,
BD2 = BC2 + CD2
| BY Pythagoras Thereom
= (12)2 + (5)2 = 144 + 25 = 169![]()
For ΔABD
a = 13 m
b = 8 m
c = 9 m![]()
∴ Area of the ΔABD
∴ Area of the quadrilateral ABCD
= Area of ΔBCD + Area of ΔABD
= 30 m2 + 35.5 m2
= 65.5 m2 (approx.)
Hence, the park occupies the area 65.5 m2. (approx.)
Tips: -
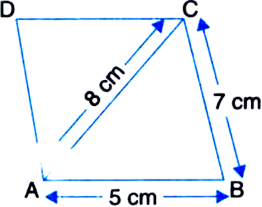
Find the area of a quadrilateral ABCD in which AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm and AC = 5 cm.
For ΔABC
a = 4 cm
b = 5 cm
c = 3 cm
∵ a2 + c2 = b2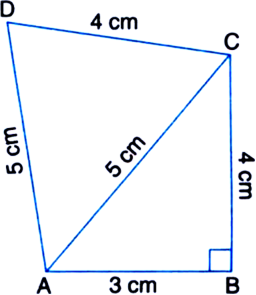
∴ ΔABC is right angled with ∠B = 90°.
∴ Area of right triangle ABC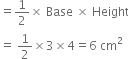
For ΔACD
a = 4 cm b = 5 cm
c = 5 cm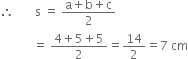
∴ Area of the ΔACD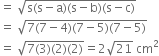
= 2 x 4.6 cm2 (approx.)
= 9.2 cm2 (approx.)
∴ Area of the quadrilateral ABCD
= Area of ΔABC + Area of ΔACD
= 6 cm2 + 9.2 cm2
= 15.2 cm2, (approx.)
Radha made a picture of an aeroplane with coloured paper as shown in figure. Find the total area of the paper used.
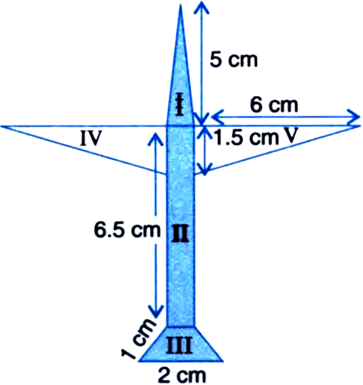
For Triangular Area I
a = 5 cm b = 5 cm c = 1 cm![]()
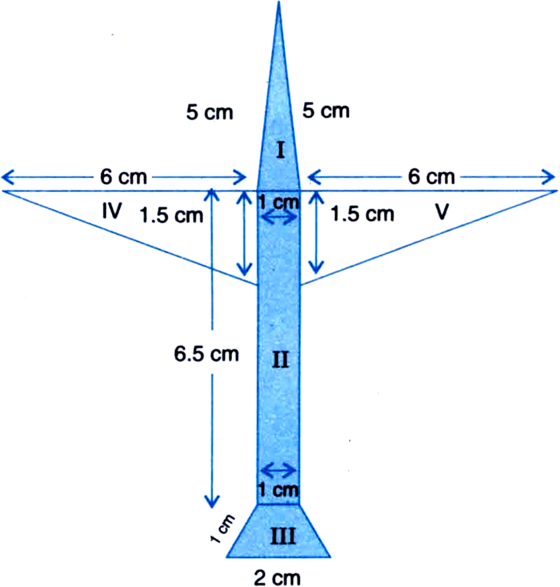
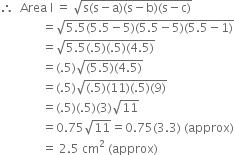
Area II = 6.5 x 1 = 6.5 cm2
For Area III
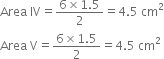
Total area of the paper used
= Area I + Area II + Area III + Area IV + Area V
= 2.5 cm2 + 6.5 cm2 + 1.3 cm2 + 4.5 cm2 + 4.5 cm2
= 19.3 cm2.
A triangle and a parallelogram have the same base and the same area. If the sides of the triangle are 26 cm, 28 cm and 30 cm, and the parallelogram stands on the base 28 cm, find the height of the parallelogram.
For triangle
a = 26 cm
b = 28 cm
c = 30 cm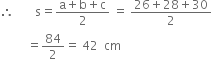
![]() Area of the triangle
Area of the triangle
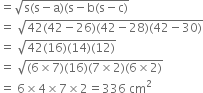
Let the height of the parallelogram be h cm.
Then, area of the parallelogram
= Base x Height = 28 x h cm2
According to the question,
![]()
Hence, the height of the parallelogram is 12 cm.
A rhombus shaped field has green grass for 18 cows to graze. If each side of the rhombus is 30 m and its longer diagonal is 48 m, how much area of grass field will each cow be getting?
For ΔABC
a = 30 m
b = 48 m
c = 30 m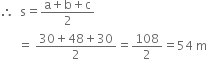
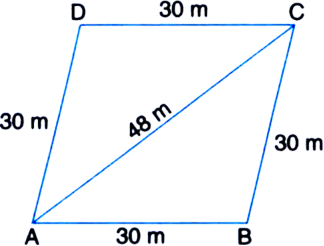
![]() Area of
Area of ![]()
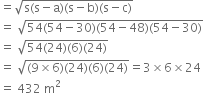
Area of the rhombus
= 2 Area of ΔABC = 2 x 432 = 864 m2
∴ Area of grass for 18 cows = 864 m2. ∴ Area of grass for 1 cow![]()
Aliter : Draw BE ⊥ AC. Then E is the midpoint of AC.![]()
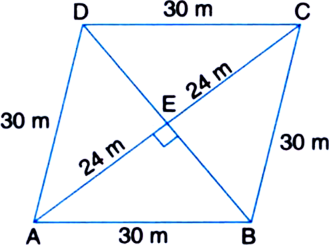
In right triangle AEB.
AB2 = AE2 + BE2
I By Pythagoras Theorem ⇒ (30)2 = (24)2 + BE2
⇒ 900 = 576 + BE2
⇒ BE2 = 900 – 576
⇒ BE2 = 324![]()
BD = 2 BE = 2 x 18 = 36 m Area of rhombus ABCD
![]() Product of diagonals
Product of diagonals
![]()
Area of right ![]()
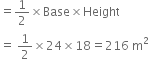
∴ Area of rhombus ABCD = 4 Area of ΔAEB = 4 x 216 = 864 m2
∴ Area of grass for 18 cows = 864 m2
![]() Area of grass for 1 cow =
Area of grass for 1 cow = ![]()
Sponsor Area
An umbrella is made by stitching 10 triangular pieces of cloth of two different colours (see figure), each piece measuring 20 cm, 50 cm and 50 cm: How much cloth of each colour is required for the umbrella?

For one triangular piece
a = 20 cm b = 50 cm c = 50 cm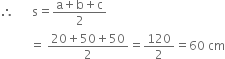
Area of one triangle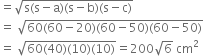
∴ Area of five triangles of one colour![]()
Hence, 1000![]() cm2 of each colour is required for the umbrella.
cm2 of each colour is required for the umbrella.
A kite in the shape of a square with a diagonal 32 cm and an isoscales triangle of base 8 cm and side 6 cm each is to be made of three different shades as shown in figure. How much paper of each shade has been used in it?
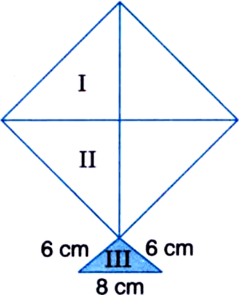
Area of paper of shade II = 256 cm2 For paper of shade III
a = 8 cm b = 6 cm c = 6 cm![]()
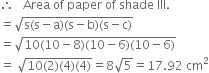
A floral design on a floor is made up of 16 tiles which are triangular, the sides of the triangle being 9 cm, 28 cm and 35 cm. Find the cost of polishing the tiles at the rate of 50 p per cm2.

For one tile
a = 9 cm b = 28 cm c = 35 cm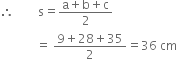
![]() Area of one tile
Area of one tile
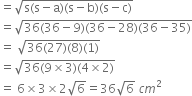
![]() Area of 16 tiles
Area of 16 tiles
![]()
∴ Cost of polishing the tiles at the rate of 50 p per cm2.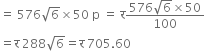
A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m. The non-parallel sides are 14 m and 13 m. Find the area of the field.
Let the given field be in the shape of a trapezium ABCD in which AB = 25 m, CD = 10 m, BC = 13 m and AD = 14 m.
From D, draw DE || BC meeting AB at E. Also, draw DF ⊥ AB.
∴ DE = BC = 13 m
AE = AB – EB = AB – DC
= 25 – 10= 15 m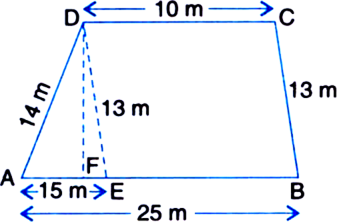
For ΔAED
a = 14 m b = 13 m c = 15 m![]()
∴ Area of the ΔAED
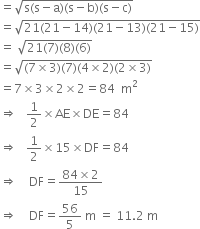
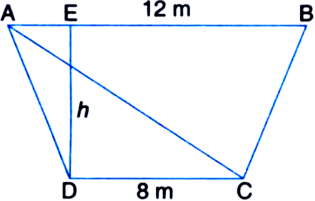
⇒ Height of the trapezium is 11.2 m. ∴ Area of parallelogram EBCD = Base x Height![]()
Area of the field = Area of ∴AED + Area of parallelogram EBCD
= 84 m2 + 112 m2 = 196 m2.
The cross-section of a canal is in the shape of a trapezium. If the canal is 12 m wide at the top and 8 m wide at the bottom and the area of its cross-section is 84 m2, determine its depth.
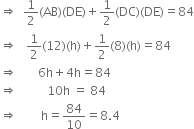
he perimeter of a rhombus is 146 cm. One of its diagonals is 55 cm. Find the length of the other diagonal and area of the rhombus.
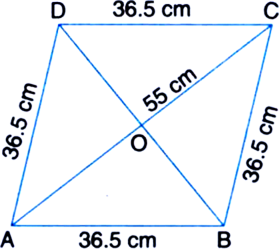
For ΔABC
a = 36.5 cm b = 55 cm c = 36.5 cm![]()
Area of the ΔABC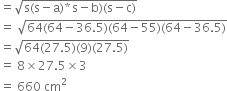
∴ Area of the rhombus ABCD
= 2 Area of the ΔABC = 2 x 660 = 1320 cm2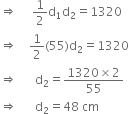
∴ Length of the other diagonal is 48 cm.
Find the area of a quadrilateral ABCD whose sides in metres are 9, 40, 28 and 15 respectively and the angle between first two sides is a right angle.
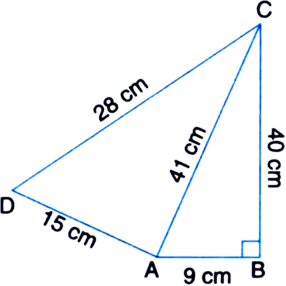
For ΔACD
a = 28 m b = 41 m c = 15 m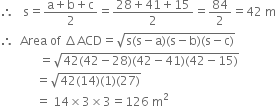
Area of the quadrilateral ABCD
= Area of ΔABC + Area of ΔACD
= 180 m2 + 126 m2 = 306 m2.
A triangle and a parallelogram have the same base and the same area. If the sides of the triangle are 15 cm, 14 cm and 13 cm and the parallelogram stands on the base 15 cm, find the height of the parallelogram.
For triangle
a = 15 cm b = 14 cm c = 13 cm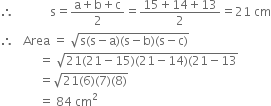
Let the height of the parallelogram be h cm. Then, area of the parallelogram
= Base x Height = 15 x h = 15h cm2 According to the question,
Area of the parallelogram
= Area of the triangle![]()
Hence, the height of the parallelogram is 5.6 cm.
The adjacent sides of a parallelogram ABCD measure 34 cm and 20 cm and the diagonal AC measures 42 cm. Find the area of the parallelogram.
For ΔABC, a = 34 cm b = 42 cm c = 20 cm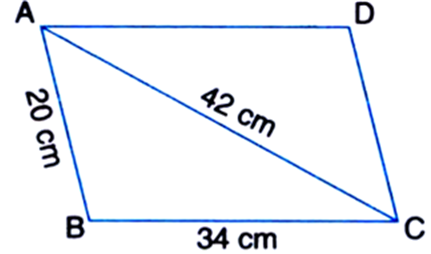
![]()
∴ Area of ΔABC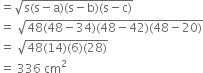
∴ Area of parallelogram ABCD
= 2 Area of triangle ABC
= 2 x 336 cm2 = 672 cm2
Find the area of a rhombus whose perimeter is 200 m and one of the diagonals is 80 m.
Let each of the equal sides of the rhombus be a cm. Then,
Perimeter = a + a + a + a = 4a m According to the question,
4a = 200![]()
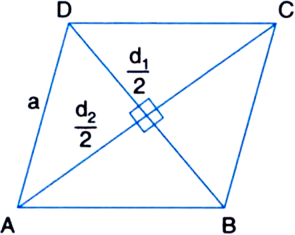
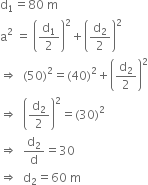
∴ Area of the rhombus![]()
Find the area of a quadrilateral ABCD whose sides AB = 13 cm, BC = 12 cm, CD = 9 cm, DA = 14 cm and diagonal BD = 15 cm.
For ∴ABD
a = 13 cm b = 14 cm c = 15 cm
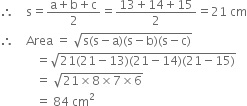
For ΔBCD
a = 9 cm b = 12 cm c = 15 cm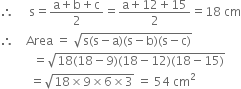
Now, area of quadrilateral ABCD
= area of ΔABD + area of ΔBCD = 84 cm2 + 54 cm2
= 138 cm2
Kamla has a triangular field with sides 240 m, 200 m, 360 m, where she grew wheat. In another triangular field with sides 240 m, 320 m, 400 m adjacent to the previous field, she wanted to grow potatoes and onions. She divided the field in two parts by joining the mid-point of the longest side to the opposite vertex and grew potatoes in one part and onions in the other part. How much area (in hectares) has been used for wheat, potatoes and onions? (1 hectare = 10000 m2).
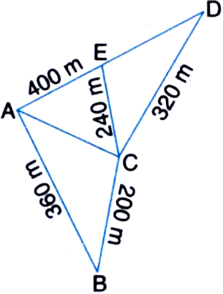
Solution not provided.
Ans. 2.26 hectares (nearly), 1.92 hectares (nearly), 1.92 hectares (nearly)
Students of a school staged a rally for cleanliness campaign. They walked through the lanes in two groups. One group walked through the lanes AB, BC and CA; while the other through AC, CD and DA. Then they cleaned the area enclosed within their lanes. If AB = 9 m, BC = 40 m, CD = 15 m, DA = 28 m and ≁B = 90°, which group cleaned more area and by how much? Find the total area cleaned by the students.
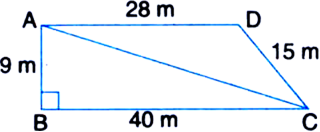
Solution not provided.
Ans. First group cleaned more area by 54 m2 ; 306 m2.
Area of a quadrilateral =
-
 x a diagonal x sun of the perpendiculats on the diagonal
x a diagonal x sun of the perpendiculats on the diagonal
-
a diagonal x sum of the perpendiculars on the diagonal
-
 x a diagonal x sun of the perpendiculats on the diagonal
x a diagonal x sun of the perpendiculats on the diagonal
-
 x a diagonal x sun of the perpendiculats on the diagonal
x a diagonal x sun of the perpendiculats on the diagonal
A.
Area of a parallelogram =
-
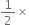 Base x Height
Base x Height
-
Base x Height
-
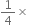 Base x Height
Base x Height
-
 Base x Height
Base x Height
Base x Height
A.
Area of a rhombus =
-
 x product of diagonals
x product of diagonals
-
product of diagonals
-
 x product of diagonals
x product of diagonals
-
 x product of diagonals
x product of diagonals
product of diagonals
A.
Area of a trapezium =
-
 x sum of parallel sides x distance between the parallel sides.
x sum of parallel sides x distance between the parallel sides.
-
Sum of parallel sides x distance between the parallel sides
-
 x sum of the parallel sides x distance between the parallel sides
x sum of the parallel sides x distance between the parallel sides
-
None of these
None of these
A.
Sponsor Area
The sides of a triangular park are in the ratio 3 : 5 : 7 and its perimeter is 300 m. Find its area.
Solution not provided.
Ans. ![]()
The sides of a triangular plot are 50 m, 65 m and 65 m. Find the cost of laying grass in this plot at the rate of र 7 per m2.
Solution not provided.
Ans. र 10500
The sides of a triangle are in the ratio 4 : 5 : 5 and its perimeter is 168 m. Find the area of the triangle.
Solution not provided.
Ans. 288 ![]() cm2
cm2
The sides of a triangle are in the ratio of 25 : 17 : 12 and its perimeter is 1080 cm. Find its area.
Solution not provided.
Ans. 360 cm2
Find the area of an equilateral triangle whose perimeter is 60 cm. (Using Heron’s formula).
Solution not provided.
Ans. ![]()
Sponsor Area
Find the cost of turfing a triangular field at the rate of र 5/m2 having lengths of its sides as 40 m, 70 m and 90 m. (Take √20 = 4.47).
Solution not provided.
Ans. र 6705
Find the cost of levelling a ground in the form of a triangle with sides 40 m, 70 m and 90 m at र 4 per square metre. (Use √5 = 2.24).
Solution not provided.
Ans. र 5376
The lengths of the sides of a triangle are in the ratio 3 : 4 : 5 and its perimeter is 144 cm. Find the area of the triangle.
Solution not provided.
Ans. 864 cm2
Sides of a triangle are in the ratio 5 : 12 : 13 and its perimeter is 120 cm. Find its area.
Solution not provided.
Ans. 480 cm2
Mock Test Series
Sponsor Area
Sponsor Area