Find the area of a rhombus whose perimeter is 200 m and one of the diagonals is 80 m.

Solution

Let each of the equal sides of the rhombus be a cm. Then,
Perimeter = a + a + a + a = 4a m According to the question,
4a = 200
$rightwards double arrow space space space space space space space space space space space space space space space straight a equals 200 over 4 equals 50 space straight m$

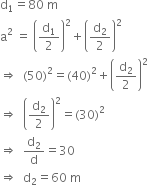
$straight d subscript 1 equals 80 space straight m straight a squared space equals space open parentheses straight d subscript 1 over 2 close parentheses squared plus open parentheses straight d subscript 2 over 2 close parentheses squared rightwards double arrow space space left parenthesis 50 right parenthesis squared equals left parenthesis 40 right parenthesis squared plus open parentheses straight d subscript 2 over 2 close parentheses squared rightwards double arrow space space open parentheses straight d subscript 2 over 2 close parentheses squared equals left parenthesis 30 right parenthesis squared rightwards double arrow space space straight d subscript 2 over straight d equals 30 rightwards double arrow space space straight d subscript 2 equals 60 space straight m$
∴ Area of the rhombus
$equals 1 half straight d subscript 1 straight d subscript 2 equals 1 half cross times 80 cross times 60 equals space 2400 space straight m squared$

For Daily Free Study Material Join wiredfaculty

Statistics

Find the area of a rhombus whose perimeter is 200 m and one of the diagonals is 80 m.

Some More Questions From Statistics Chapter

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

Phone Number

Email Address

Loaction