Question
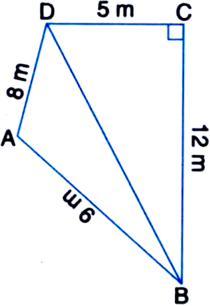
A park, in the shape of a quadrilateral ABCD, has ∠C = 90°, AB = 9 m, BC = 12 m, CD = 5 m and AD = 8 m. How much area does it occupy?
Solution
Join BD.
Area of right triangle BCD
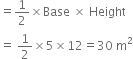
In right triangle BCD,
BD2 = BC2 + CD2
| BY Pythagoras Thereom
= (12)2 + (5)2 = 144 + 25 = 169![]()
For ΔABD
a = 13 m
b = 8 m
c = 9 m![]()
∴ Area of the ΔABD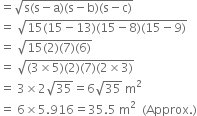
∴ Area of the quadrilateral ABCD
= Area of ΔBCD + Area of ΔABD
= 30 m2 + 35.5 m2
= 65.5 m2 (approx.)
Hence, the park occupies the area 65.5 m2. (approx.)
Tips: -



