Question
A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m. The non-parallel sides are 14 m and 13 m. Find the area of the field.
Solution
Let the given field be in the shape of a trapezium ABCD in which AB = 25 m, CD = 10 m, BC = 13 m and AD = 14 m.
From D, draw DE || BC meeting AB at E. Also, draw DF ⊥ AB.
∴ DE = BC = 13 m
AE = AB – EB = AB – DC
= 25 – 10= 15 m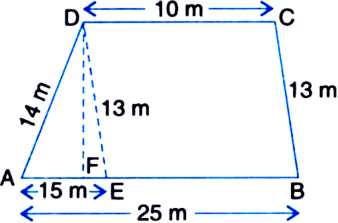
For ΔAED
a = 14 m b = 13 m c = 15 m![]()
∴ Area of the ΔAED
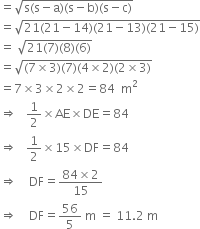
⇒ Height of the trapezium is 11.2 m. ∴ Area of parallelogram EBCD = Base x Height![]()
Area of the field = Area of ∴AED + Area of parallelogram EBCD
= 84 m2 + 112 m2 = 196 m2.



