Question

he perimeter of a rhombus is 146 cm. One of its diagonals is 55 cm. Find the length of the other diagonal and area of the rhombus.

Solution

Length of a side of the rhombus

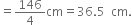
equals 146 over 4 cm equals 36.5 space space cm.

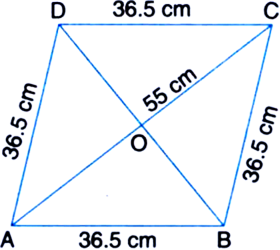
For ΔABC
a = 36.5 cm b = 55 cm c = 36.5 cm
$therefore space space space space space space space space space space space straight s equals fraction numerator straight a plus straight b plus straight c over denominator 2 end fraction equals fraction numerator 36.5 plus 55 plus 36.5 over denominator 2 end fraction equals 128 over 2 space space space space space space space space space space space space space space equals 64 space space cm$
Area of the ΔABC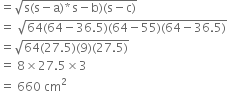
$equals square root of straight s left parenthesis straight s minus straight a right parenthesis asterisk times straight s minus straight b right parenthesis left parenthesis straight s minus straight c right parenthesis end root equals space square root of 64 left parenthesis 64 minus 36.5 right parenthesis left parenthesis 64 minus 55 right parenthesis left parenthesis 64 minus 36.5 right parenthesis end root equals square root of 64 left parenthesis 27.5 right parenthesis left parenthesis 9 right parenthesis left parenthesis 27.5 right parenthesis end root equals space 8 cross times 27.5 cross times 3 equals space 660 space cm squared$

∴ Area of the rhombus ABCD
= 2 Area of the ΔABC = 2 x 660 = 1320 cm²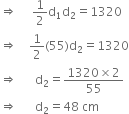 $rightwards double arrow space space space space space 1 half straight d subscript 1 straight d subscript 2 equals 1320 rightwards double arrow space space space space 1 half left parenthesis 55 right parenthesis straight d subscript 2 equals 1320 rightwards double arrow space space space space space space straight d subscript 2 equals fraction numerator 1320 cross times 2 over denominator 55 end fraction rightwards double arrow space space space space space space straight d subscript 2 equals 48 space cm$
∴ Length of the other diagonal is 48 cm.

For Daily Free Study Material Join wiredfaculty

Statistics

he perimeter of a rhombus is 146 cm. One of its diagonals is 55 cm. Find the length of the other diagonal and area of the rhombus.

Some More Questions From Statistics Chapter

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

Phone Number

Email Address

Loaction