Question
Find the area of a quadrilateral ABCD whose sides in metres are 9, 40, 28 and 15 respectively and the angle between first two sides is a right angle.
Solution
For ΔABC Area of right triangle ABC
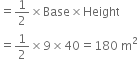
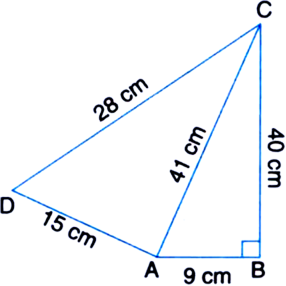
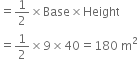

For ΔACD
a = 28 m b = 41 m c = 15 m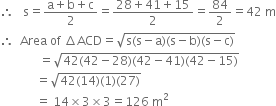
Area of the quadrilateral ABCD
= Area of ΔABC + Area of ΔACD
= 180 m2 + 126 m2 = 306 m2.



