Question
A triangle and a parallelogram have the same base and the same area. If the sides of the triangle are 26 cm, 28 cm and 30 cm, and the parallelogram stands on the base 28 cm, find the height of the parallelogram.
Solution
For triangle
a = 26 cm
b = 28 cm
c = 30 cm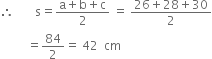
Area of the triangle
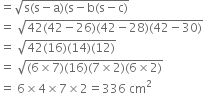
Let the height of the parallelogram be h cm.
Then, area of the parallelogram
= Base x Height = 28 x h cm2
According to the question,
Hence, the height of the parallelogram is 12 cm.
