A retired person wants to invest an amount of Rs. 50, 000. His broker recommends investing in two type of bonds ‘A’ and ‘B’ yielding 10% and 9% return respectively on the invested amount. He decides to invest at least Rs. 20,000 in bond ‘A’ and at least Rs. 10,000 in bond ‘B’. He also wants to invest at least as much in bond ‘A’ as in bond ‘B’. Solve this linear programming problem graphically to maximise his returns.
Maximize Z = 0.1x + 0.09 y
x + y ≤ 50000
x ≥ 20000
y ≥ 10000
y ≤ x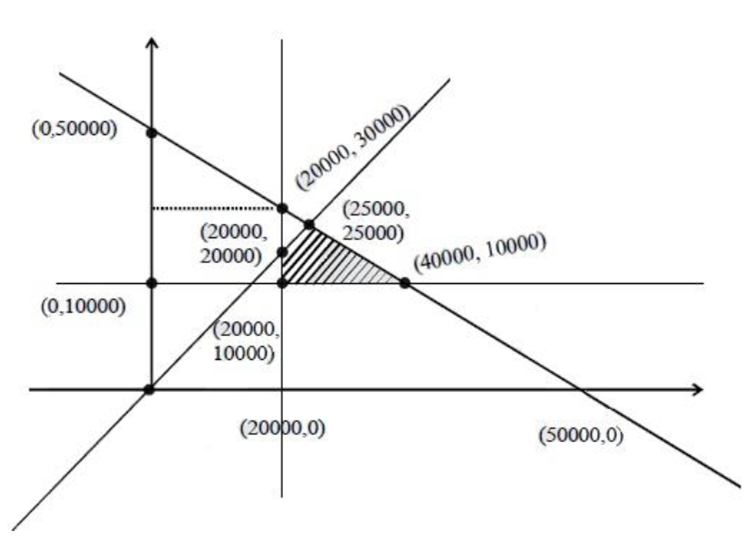
|
|
z=0.1 x+0.09y |
|
P1 (20000,10000) |
2900 |
|
P2(40000,10000) |
4900 |
|
P3(25000,25000) |
4750 |
|
P4(20000,20000) |
3800 |
when A invest 400000 & B invest 10000 his return is maximum.