Sponsor Area
Application Of Integrals
Using integration, find the area of the region enclosed between the two circles: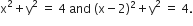
Given equations of the circles are: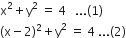
Equation (1) is a circle with centre O at the origin and radius 2. Equation (2) is a circle with centre C(2, 0) and radius 2.
Solving (1) and (2), we have: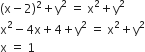
This gives 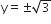
Thus, the points of intersection of the given circles are 
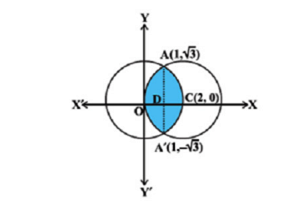
Required area
= Area of the region OACA'O
= 2[area of the region ODCAO]
=2[area of the region ODAO + area of the region DCAD]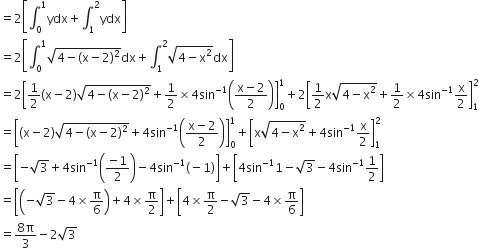
Some More Questions From Application of Integrals Chapter
A small firm manufactures necklaces and bracelets. The total number of necklaces and bracelets that it can handle per day is at most 24. It takes one hour to make a bracelet and half an hour to make a necklace. The maximum number of hours available per day is 16. If the profit on a necklace is ` 100 and that on a bracelet is ` 300. Formulate on L.P.P. for finding how many of each should be produced daily to maximize the profit? It is being given that at least one of each must be produced.
Solve the following L.P.P. graphically :
Minimise Z = 5x + 10y
Subject to x + 2y ≤ 120
Constraints x + y ≥ 60
x – 2y ≥ 0
and x, y ≥ 0
Minimise Z = 5x + 10y
Subject to x + 2y ≤ 120
Constraints x + y ≥ 60
x – 2y ≥ 0
and x, y ≥ 0
The line L1: y = x = 0 and L2: 2x + y = 0 intersect the line L3: y + 2 = 0 at P and Q respectively. The bisectorof the acute angle between L1 and L2 intersects L3 at R.
Statement-1: The ratio PR: RQ equals 2√2:√5
Statement-2: In any triangle, the bisector of an angle divides the triangle into two similar triangles.
Statement-1: The ratio PR: RQ equals 2√2:√5
Statement-2: In any triangle, the bisector of an angle divides the triangle into two similar triangles.
Sponsor Area
Mock Test Series
Mock Test Series





