+91-8076753736 [email protected]

-->

Application Of Integrals

Question

Wired Faculty App

Solve the following L.P.P. graphically :
Minimise Z = 5x + 10y
Subject to x + 2y ≤ 120
Constraints x + y ≥ 60
x – 2y ≥ 0
and x, y ≥ 0

Solution

The corner points of the feasible region are A(60,0), B (120,0), C(60,30), and D (40,20).
The vaules of Z at these corner points are as follows.

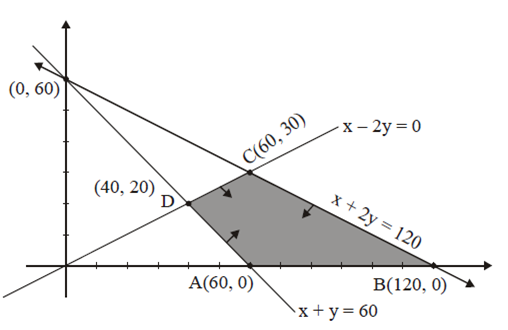
The corner points of the feasible region are A(60,0), B (120,0), C(60,30), and D (40,20).
The values of Z at these corner points are as follows.

Z = 5x +10y
Z|_A(60,0) =300
Z|_B(120,0) = 600
Z|_C(60,30) =600
Z|_D(40,20) =400
Minimum value of Z = 300 at x = 60, y =0

Some More Questions From Application of Integrals Chapter

A small firm manufactures necklaces and bracelets. The total number of necklaces and bracelets that it can handle per day is at most 24. It takes one hour to make a bracelet and half an hour to make a necklace. The maximum number of hours available per day is 16. If the profit on a necklace is ` 100 and that on a bracelet is ` 300. Formulate on L.P.P. for finding how many of each should be produced daily to maximize the profit? It is being given that at least one of each must be produced.

Solve the following L.P.P. graphically :
Minimise Z = 5x + 10y
Subject to x + 2y ≤ 120
Constraints x + y ≥ 60
x – 2y ≥ 0
and x, y ≥ 0

The line L₁: y = x = 0 and L₂: 2x + y = 0 intersect the line L₃: y + 2 = 0 at P and Q respectively. The bisectorof the acute angle between L₁ and L₂ intersects L₃ at R.
Statement-1: The ratio PR: RQ equals 2√2:√5
Statement-2: In any triangle, the bisector of an angle divides the triangle into two similar triangles.

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation