Sponsor Area
Application Of Integrals
Question
Minimum and maximum z = 5x + 2y subject to the following constraints:
x – 2y ≤ 2
3x + 2y ≤ 12
−3x + 2y ≤ 3
x ≥ 0, y ≥ 0
Solution
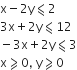
Converting the inequations into equations, we obtain the lines
x – 2y = 2…..(i)
3x + 2y = 12……(ii)
−3x + 2y = 3……(iii)
x = 0, y = 0
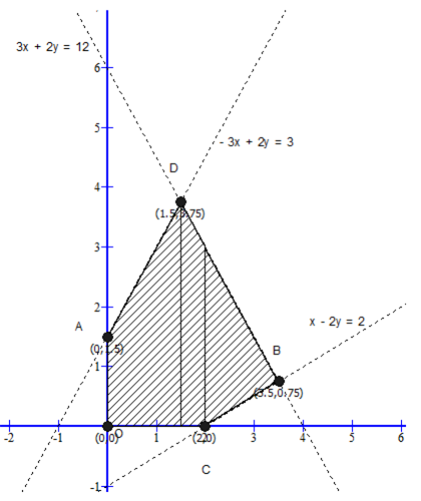
From the graph, we get the corner points as
A(0, 5), B(3.5, 0.75), C(2, 0), D(1.5, 3.75), O(0, 0)
The values of the objective function are:
| Point (x,y) | Values of the objective function Z= 5x+2y |
| A(0, 5) | 5 × 0 + 2 × 5 = 10 |
| B(3.5, 0.75) | 5 x 3.5 +2 x 0.75 =19 (Maximum) |
| C(2, 0) | 5 x 1.5 +2 x 3.75 =15 |
| O(0,0) | 5 x 0 + 2 x 0 = 0 (Minimum) |
The maximum value of Z is 19 and its minimum value is 0.
Some More Questions From Application of Integrals Chapter
The line L1: y = x = 0 and L2: 2x + y = 0 intersect the line L3: y + 2 = 0 at P and Q respectively. The bisectorof the acute angle between L1 and L2 intersects L3 at R.
Statement-1: The ratio PR: RQ equals 2√2:√5
Statement-2: In any triangle, the bisector of an angle divides the triangle into two similar triangles.
Statement-1: The ratio PR: RQ equals 2√2:√5
Statement-2: In any triangle, the bisector of an angle divides the triangle into two similar triangles.
Sponsor Area
Mock Test Series
Mock Test Series