Using integration find the area of the region bounded by the parabola y² = 4x and the circle 4x² + 4y² = 9.

The respective equations for the parabola and the circle are:

$$\begin{gathered} {\mathrm{y}}^2 = 4\mathrm{x} ............\left(1\right) \\ 4{\mathrm{x}}^2 + 4{\mathrm{y}}^2 = 9 ............\left(2\right) \\ \mathrm{or} {\mathrm{x}}^2 + {\mathrm{y}}^2 ={\left(\frac{3}{2}\right)}^2 \end{gathered}$$

Equations (1) is a parabola with vertex ( 0, 0 ) which opens to the right and  equation (2) is a circle with centre (0, 0 ) and radius $\frac{3}{2}$.

From equations (1) and (2), we get:

$$\begin{gathered} 4{\mathrm{x}}^2 + 4 ( 4\mathrm{x} ) = 9 \\ 4{\mathrm{x}}^2 + 16\mathrm{x} - 9 = 0 \\ 4{\mathrm{x}}^2 + 18\mathrm{x} - 2\mathrm{x}- 9 = 0 \\ 2\mathrm{x} ( 2\mathrm{x} + 9 ) - 1 ( 2\mathrm{x} + 9 ) = 0 \\ ( 2\mathrm{x} + 9 ) ( 2\mathrm{x} - 1 ) = 0 \\ \mathrm{x} = -\frac{9}{2}, \frac{1}{2} \\ \mathrm{For} \mathrm{x} = -\frac{9}{2}, {\mathrm{y}}^2 = 4 \left(-\frac{9}{2}\right), \mathrm{which} \mathrm{is} \mathrm{not} \mathrm{possible}, \mathrm{hence} \mathrm{x} = \frac{1}{2} \\ \mathrm{Therefore}, \mathrm{the} \mathrm{given} \mathrm{curves} \mathrm{intersect} \mathrm{at} \mathrm{x} = \frac{1}{2}. \end{gathered}$$

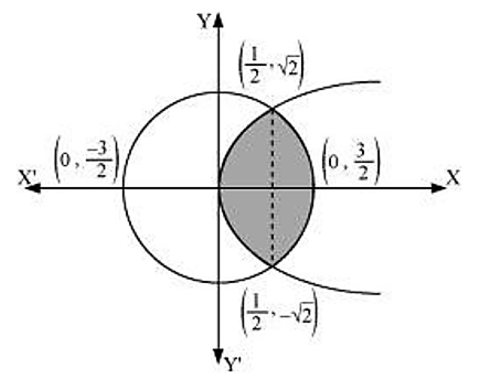
Required area of the region bound by the two curves

$$\begin{gathered} = 2 {\int }_0^{\frac{1}{2}} 2\sqrt{\mathrm{x}}\mathrm{dx} + 2 {\int }_{\frac{1}{2}}^{\frac{3}{2}} \sqrt{\frac{9}{4} - {\mathrm{x}}^2} \mathrm{dx} \\ = 4 {\left[\frac{2}{3} {\mathrm{x}}^{\frac{3}{2}}\right]}_0^{\frac{1}{2}} + 2 {\left[\frac{\mathrm{x}}{2} \sqrt{\frac{9}{4} - {\mathrm{x}}^2} + \frac{9}{8} {\sin }^{-1} \left(\frac{2\mathrm{x}}{3}\right)\right]}_{\frac{1}{2}}^{\frac{3}{2}} \\ = \frac{8}{3}{\left(\frac{1}{8}\right)}^{\frac{1}{2}} + 2 \left[ 0 +\frac{9}{8} {\sin }^{-1} 1 - \frac{1}{4} \sqrt{2} - \frac{9}{8} {\sin }^{-1} \left(\frac{1}{3}\right)\right] \\ = \frac{8}{3}\left(\frac{1}{2\sqrt{2}}\right) + \frac{9}{4} \left(\frac{\mathrm{\pi }}{2}\right) - \frac{\sqrt{2}}{2} - \frac{9}{4} {\sin }^{-1} \left(\frac{1}{3}\right) \\ = \frac{2\sqrt{2}}{3} + \frac{9\mathrm{\pi }}{8} - \frac{\sqrt{2}}{2} -\frac{9}{4} {\sin }^{-1} \left(\frac{1}{3}\right) \end{gathered}$$