Prove that the curves y²= 4x and x²= 4y divide the area of the square bonded by x = 0, x = 4, y = 4, and y = 0 into three equal parts.

The point of intersection of the 

Parabolas  y² = 4x   and   x² = 4y are ( 0, 0 ) and ( 4, 4 )

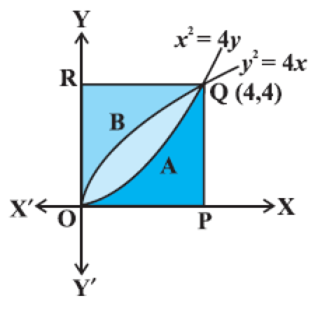
Now the area of the region OAQBO bounded by curves  y² = 4x  and  x² = 4y, 

$$\begin{gathered} {\int }_0^4\left( 2 \sqrt{\mathrm{x}} - \frac{{\mathrm{x}}^2}{4}\right) \mathrm{dx} = {\left[ 2 \frac{{\mathrm{x}}^{{\displaystyle \frac{3}{2}}}}{{\displaystyle \frac{3}{2}}} - \frac{{\mathrm{x}}^3}{12}\right]}_0^4 = \frac{32}{3} - \frac{16}{3} = \frac{16}{3}\mathrm{sq}. \mathrm{units} \\ ..............\left(\mathrm{i}\right) \end{gathered}$$

Again, the area of the region OPQAO bounded by the curve  x² = 4y ,  x = 0,

x = 4  and  the  x - axis,

${\int }_0^4 \frac{{\mathrm{x}}^2}{4} \mathrm{dx} = {\left[\frac{{\mathrm{x}}^3}{12}\right]}_0^4 = \left(\frac{64}{12}\right) = \frac{16}{3} \mathrm{sq}. \mathrm{units} ..............\left(\mathrm{ii}\right)$

Similarly, the area of the region OBQRO bounded by the curve y² = 4x, the y-axis, y = 0  and  y = 4

${\int }_0^4 \frac{{\mathrm{y}}^2}{4} \mathrm{dy} = {\left[\frac{{\mathrm{y}}^3}{12}\right]}_0^4 = \frac{16}{3} \mathrm{sq}. \mathrm{units} ............\left(\mathrm{iii}\right)$

From (i), (ii), and (iii) it is concluded that the area of the region OAQBO =

area of the region OPQAO = area of the region OBQRO, i. e., area bounded

by parabolas  y² = 4x  and  x² = 4y  divides the area of the square into

three equal parts.