गणित Chapter 2 बहुपद
Sponsor Area
NCERT Solution For Class 10 गणित गणित
किसी बहुपद p(x) के लिए y = P(x) का ग्राफ आकृति में दिया हैl प्रत्येक स्थिति में, P(x) के शुन्यकों की संख्या ज्ञात कीजिएl
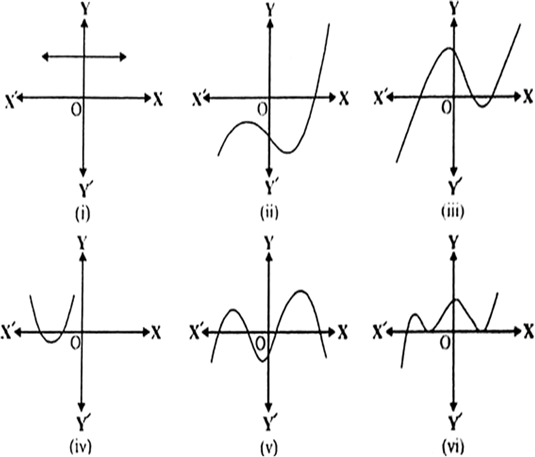
(i) क्योंकि ग्राफ x-अक्ष को प्रतिच्छेद नहीं करता, इसलिए यहाँ पर कोई शून्यक नहीं हैl
(ii) शून्यक की संख्या 1 है, क्योंकि यहाँ पर ग्राफ x-अक्ष को केवल एक बिन्दु पर प्रतिच्छेद करता हैl
(iii) शून्यक की संख्या 3 है, क्योंकि यहाँ पर ग्राफ x-अक्ष को केवल 3 बिन्दुओं पर प्रतिच्छेद करता हैl
(iv) शून्यक की संख्या 2 है, क्योंकि यहाँ पर ग्राफ x-अक्ष को केवल 2 बिन्दुओं पर प्रतिच्छेद करता हैl
(v) शून्यक की संख्या 4 है, क्योंकि यहाँ पर ग्राफ x-अक्ष को केवल 4 बिन्दुओं पर प्रतिच्छेद करता हैl
(vi) शून्यक की संख्या 3 है, क्योंकि यहाँ पर ग्राफ x-अक्ष को केवल 3 बिन्दुओं पर प्रतिच्छेद करता हैl
निम्नलिखित द्विघात बहुपदों के शून्यक ज्ञात कीजिए और शुन्यकों तथा गुणांकों के बीच के सम्बन्ध की सत्यता की जाँच कीजिए:
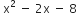
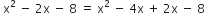
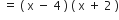
अत; बहुपद x2 – 2x - 8 x = 4 or x = –2.
Therefore, the zeroes of x2 – 2x – 8 के शून्यक 4 और - 2 है
शुन्यकों का योग = (4) + (-2)
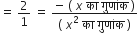
2 = 2
शुन्यकों का गुणनफल = (4) x (-2)
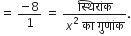
- 8 = - 8
निम्नलिखित द्विघात बहुपदों के शून्यक ज्ञात कीजिए और शुन्यकों तथा गुणांकों के बीच के सम्बन्ध की सत्यता की जाँच कीजिए:
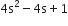
= 2s ( 2s - 1 ) - 1 ( 2s - 1 )
= (2s–1)(2s– 1)

अत:
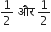 दिए हुए बहुपद के शून्यक हैl
दिए हुए बहुपद के शून्यक हैlशुन्यकों का योग =
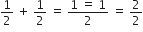
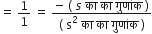 =
= 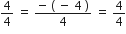
शुन्यकों का गुणनफल =
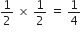
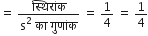
निम्नलिखित द्विघात बहुपदों के शून्यक ज्ञात कीजिए और शुन्यकों तथा गुणांकों के बीच के सम्बन्ध की सत्यता की जाँच कीजिए:
6x2 - 3 - 7x
6x2 – 7x – 3 = 6x2 – 9x + 2x – 3
= 3 x ( 2x – 3 ) + 1 ( 2x – 3 )
= (3x + 1) (2x – 3 )
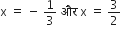
अत: दिए गए बहुपद के शून्यक है 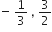
शुन्यकों का योग = 

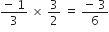
=

निम्नलिखित द्विघात बहुपदों के शून्यक ज्ञात कीजिए और शुन्यकों तथा गुणांकों के बीच के सम्बन्ध की सत्यता की जाँच कीजिए:
4u2 8u = 0
4u2 + 8u = 4u ( u + 2 )
4u = 0 , u + 2 = 0
तो, u = 0 , - 2
अत; दिए गए बहुपद के शून्यक हैं 0 और - 2
शुन्यकों का योग = 0 + (-2) = 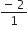 =
= 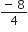
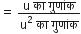
शुन्यकों का गुणनफल = 0 ( - 2 ) = 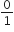
= 
निम्नलिखित द्विघात बहुपदों के शून्यक ज्ञात कीजिए और शुन्यकों तथा गुणांकों के बीच के सम्बन्ध की सत्यता की जाँच कीजिए:
t2 - 15
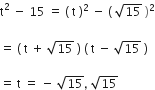
अत: दिए गए बहुपद के शून्यक है 
शुन्यकों का योग = 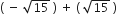
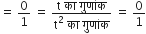
शुन्यकों का गुणनफल = 
= 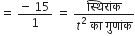
निम्नलिखित द्विघात बहुपदों के शून्यक ज्ञात कीजिए और शुन्यकों तथा गुणांकों के बीच के सम्बन्ध की सत्यता की जाँच कीजिए:
3x2 - x - 4
3x2 – x – 4 = 3x2 – 4x + 3x – 4
= x ( 3x – 4 ) + 1 ( 3x – 4 )
= ( x+ 1 ) ( 3x – 4 ) और
और 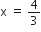
शुन्यकों का योग = 
= 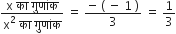
शुन्यकों का गुणनफल = 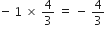

एक द्विघात बहुपद ज्ञात कीजिए, जिसके शुन्यकों के योग तथा गुणनफल क्रमश: दी गई संख्याएँ है:
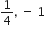
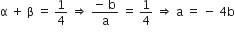
और

यदि
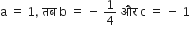
इसलिए, एक द्विघात बहुपद जो दी गई संख्याओं के अनुरूप है:
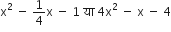
एक द्विघात बहुपद ज्ञात कीजिए, जिसके शुन्यकों के योग तथा गुणनफल क्रमश: दी गई संख्याएँ है:
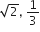
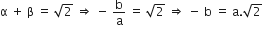
और
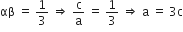
और
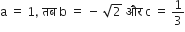
इसलिए, एक द्विघात बहुपद जो दी गई संख्या के अनुरूप है:

एक द्विघात बहुपद ज्ञात कीजिए, जिसके शुन्यकों के योग तथा गुणनफल क्रमश: दी गई संख्याएँ है:
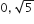
माना द्विघात बहुपद है: ax2 + bx + c, और इसके शून्यक α और β हैं, तब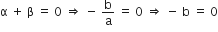
और 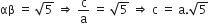
यदि 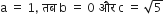
इसलिए एक द्विघात बहुपद जो दी गई संख्या क अनुरूप है:
एक द्विघात बहुपद ज्ञात कीजिए, जिसके शुन्यकों के योग तथा गुणनफल क्रमश: दी गई संख्याएँ है:
1, 1
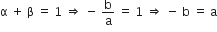
और
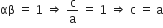
यदि a = 1, तब b = –1 और c = 1.
इसलिए एक द्विघात बहुपद जो दी गई संख्या क अनुरूप है:
x2 – x + 1
एक द्विघात बहुपद ज्ञात कीजिए, जिसके शुन्यकों के योग तथा गुणनफल क्रमश: दी गई संख्याएँ है:
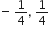
माना द्विघात बहुपद है: ax2 +bx + c, और इसके शून्यक α और β, तब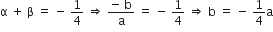
और 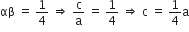
यदि a = 1, तब 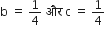
इसलिए एक द्विघात बहुपद जो दी गई संख्या क अनुरूप है:
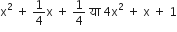
एक द्विघात बहुपद ज्ञात कीजिए, जिसके शुन्यकों के योग तथा गुणनफल क्रमश: दी गई संख्याएँ है:
4, 1
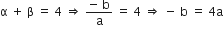
और
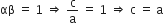
यदि a = 1, तब b = –4 और c = 1
इसलिए एक द्विघात बहुपद जो दी गई संख्या क अनुरूप है:
x2 – 4x + 1
विभाजन एल्गोरिथ्म का प्रयोग करके निम्न में से p(x) को g(x) से भाग देने पर भागफल और शेषफल ज्ञात कीजिए:
p(x) = x3 – 3x2 + 5x – 3, g(x) = x2 – 2
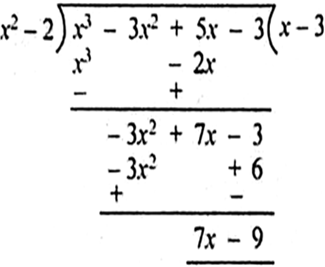
यहाँ आकर हम रुक गए, क्योंकि शेष पद की घात भाजक की घात से कम रह गईl अत: यहाँ पर भागफल = x - 3 और शेषफल = 7x - 9 हैl
विभाजन एल्गोरिथ्म का प्रयोग करके निम्न में से p(x) को g(x) से भाग देने पर भागफल और शेषफल ज्ञात कीजिए:
p(x) = x4 – 3x2 + 4x + 5, g(x) = x2 + 1 – x
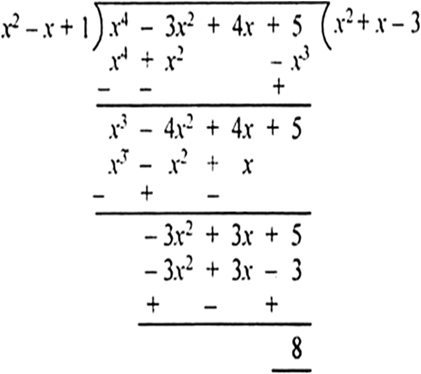
यहाँ आकर हम रुक गए, क्योंकि शेष पद की घात भाजक की घात से कम रह गईl अत: यहाँ पर भागफल = ( x2 + x - 3 ) और शेषफल = 8 हैl
विभाजन एल्गोरिथ्म का प्रयोग करके निम्न में से p(x) को g(x) से भाग देने पर भागफल और शेषफल ज्ञात कीजिए:
p(x) = x4 – 5x + 6, g(x) = 2 – x2
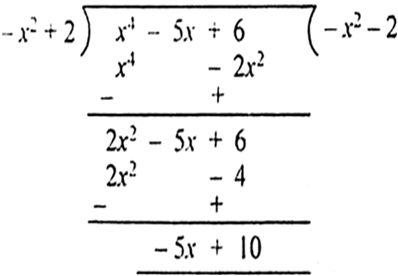
यहाँ आकर हम रुक गए, क्योंकि शेष पद की घात भाजक की घात से कम रह गईl अत: यहाँ पर भागफल = - ( x + 2 ) और शेषफल = ( - 5 + 10 ) हैl
पहले बहुपद से दूसरे बहुपद को भाग करके जाँच कीजिए कि क्या प्रथम बहुपद द्वितीय बहुपद का एक गुणनखंड हैl
t2 – 3, 2t4 + 3t3 – 2t2 – 9t – 12
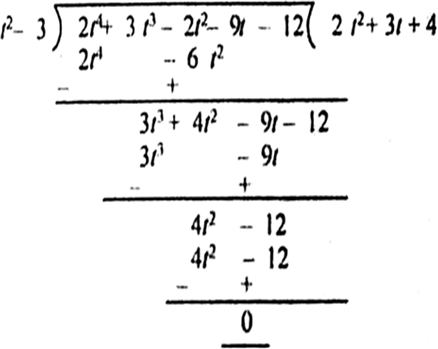
यहाँ पर, शेषफल शून्य है, अत: ( x2 + 3x + 1 ), (3x4 +5x3 - 7x2 + 2x + 2 ) का एक गुणनखंड हैl
Sponsor Area
पहले बहुपद से दूसरे बहुपद को भाग करके जाँच कीजिए कि क्या प्रथम बहुपद द्वितीय बहुपद का एक गुणनखंड हैl
x2 + 3x + 1, 3x4 + 5x3 – 7x2 + 2x + 2
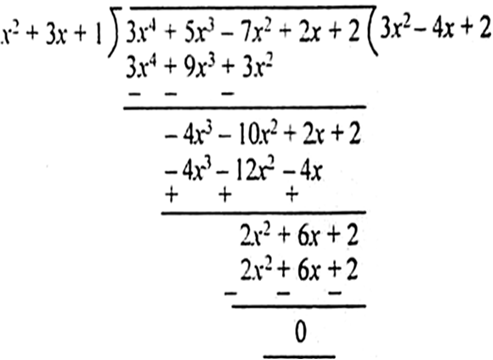
यहाँ पर शेषफल शून्य है, अत: ( x2 + 3x + 1 ), ( 3x4 + 5x3 – 7x2 + 2x + 2 ) का एक गुणनखंड हैl
पहले बहुपद से दूसरे बहुपद को भाग करके जाँच कीजिए कि क्या प्रथम बहुपद द्वितीय बहुपद का एक गुणनखंड हैl
x3 – 3x + 1, x5 –4x3 + x2 + 3x + 1
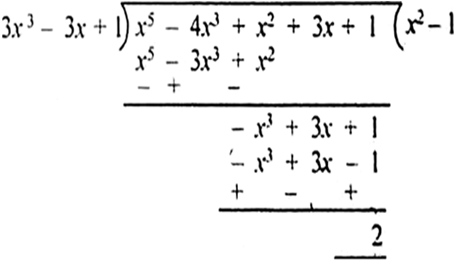
यहाँ पर शेषफल शून्य नहीं है, अत: ( x3 – 3x + 1 0, ( x5 –4x3 + x2 + 3x + 1 ) का एक गुणनखंड नहीं हैl
3x4 + 6x3 – 2x2 - 10x - 5 के अन्य सभी शून्यक ज्ञात कीजिए, यदि इसके दो शून्यक
 हैंl
हैंl
दिया है: 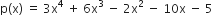 और
और 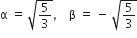
∵ दो शून्यक है 
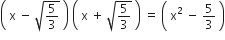 दिए हुए बहुपद p(x) का एक गुणनखंड हैl
दिए हुए बहुपद p(x) का एक गुणनखंड हैl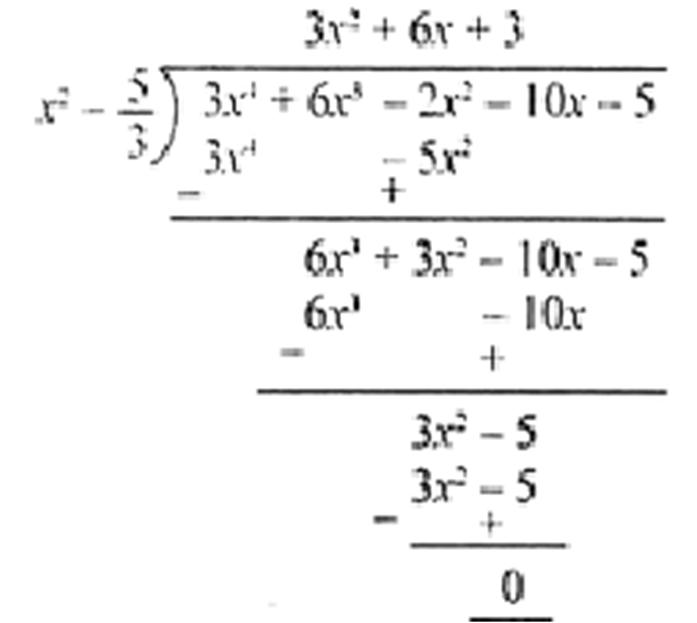
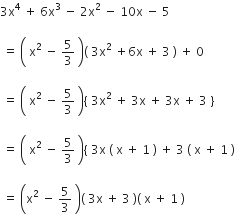
( 3x + 3 )( x + 1 ) = 3 ( x + 1 )( x + 1)
शून्यक: x = -1, -1
अत दिए हुए चतुर्थ घात बहुपद के शून्यक हैं: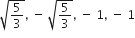
यदि x3 – 3x2 + x + 2 को एक बहुपद g(x) से भाग देने पर, भागफल और शेषफल क्रमश: x – 2 और –2x + 4 हैं तो g(x) ज्ञात कीजिएl
भाज्य p(x) x3 – 3x2 + x + 2
भाजक g(x) = ?, भागफल q(x) = x – 2, शेषफल r(x) = –2x + 4
विभाजक एल्गोरिथ्म द्वारा:
भाज्य = भागफल x भाजक + शेषफल

g(x) = x2 - x + 1
बहुपद p(x), g(x), q(x) और r(x) के ऐसे उदाहरण दीजिए, जो विभाजन एल्गोरिथ्म को संतुष्ट करते हों तथा
घात p(x) = घात q(x)
घात p(x) = घात q(x)
P(x) = 2x2 - 3
g(x) = 2
q(x) = x2 - 1
और r(x) = -1
यहाँ पर P(x) = q(x) x g(x) + r(x)
बहुपद p(x), g(x), q(x) और r(x) के ऐसे उदाहरण दीजिए, जो विभाजन एल्गोरिथ्म को संतुष्ट करते हों तथा
घात r(x) = 0
घात r(x) = 0
p(x) = 3x3 - 5
g(x) = x3
q(x) = 3
और r(x) = -5
यहाँ पर, p(x) = q(x) X g(x) + r(x)
बहुपद p(x), g(x), q(x) और r(x) के ऐसे उदाहरण दीजिए, जो विभाजन एल्गोरिथ्म को संतुष्ट करते हों तथा
घात q(x) = घात r(x)
घात q(x) = घात r(x)
p(x) = x - 5
g(x) = x - 2
q(x) = 1
और r(x) = -3
यहाँ पर, p(x) = q(x) X g(x) + r(x)
सर्यपित कीजिए कि निम्न त्रिघात बहुपदों के साथ दी गई संख्याएं शून्यक हैं प्रत्येक स्थिति में शुन्यकों और गुणकों के बीच के सम्बन्ध को सत्यापित कीजिए:
2x3 + x2 –5x + 2; 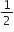 , 1,–2
, 1,–2
a = 2, b = 1, c = -5, d = 2
अब
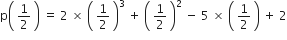
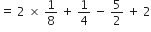
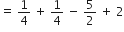
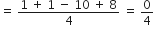
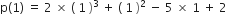
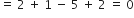
और
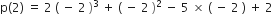
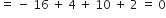
∴
 बहुपद
बहुपद 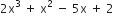 के शून्यक हैl
के शून्यक हैlअत: यह सत्यापित हुआ
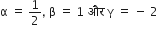
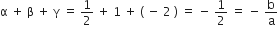
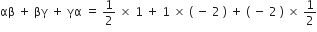
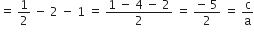
और
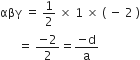
अत: सत्यापित हुआl
सर्यपित कीजिए कि निम्न त्रिघात बहुपदों के साथ दी गई संख्याएं शून्यक हैं प्रत्येक स्थिति में शुन्यकों और गुणकों के बीच के सम्बन्ध को सत्यापित कीजिए:
x3 - 4x2 + 5x - 2; 2, 1, 1
माना p(x) = x3 - 4x2 + 5x - 2
दिए हुए बहुपद की ax3 + bx2 + cx + d से तुलना करने पर, हम प्राप्त करते है:
a = 1, b = - 4, c = 5 और d = - 2
अब,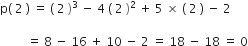
और 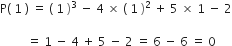
∴ 2, 1, 1 बहुपद ( x3 - 4x2 + 5x - 2 ) के शून्यक है
अत: सत्यापित हुआ
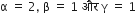
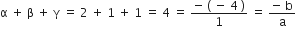
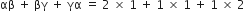
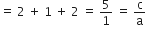
और 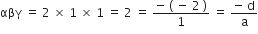
अत: सत्यापित हुआl
एक त्रिघात बहुपद ज्ञात कीजिए जिसके शुन्यकों का योग, दो शून्यक को एक साथ लेकर उनके गुणनफलों का योग तथा तीनों शुन्यकों के गुणनफल क्रमश: 2, - 7, - 14 होंl
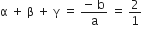
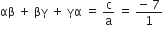
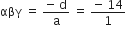
यदि a = 1, तब b = – 2, c = – 7, d = 14
x3 – 2x2 – 7x + 14
यदि बहुपद x3 – 3x2 + x + 1 के शून्यक (a – b), a, (a + b), हों तो 'a' और 'b' ज्ञात कीजिएl
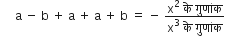
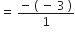

 ( a - b ) a ( a + b ) =
( a - b ) a ( a + b ) =
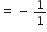
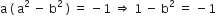

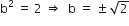
अत:,

यदि बहुपद x4 – 26x3 - 26x2 + 138x – 35 के दो शून्यक 2 ± 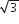 , हों, तो अन्य शून्यक ज्ञात कीजिएl
, हों, तो अन्य शून्यक ज्ञात कीजिएl

∴
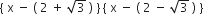

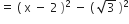
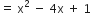 दिए हुए बहुपद का एक गुणनखंड है
दिए हुए बहुपद का एक गुणनखंड हैअब हम दिए हुए बहुपद तथा ( x2 – 4x + 1 ) पर विभाजन एल्गोरिथ्म लागू करके प्राप्त करते हैl
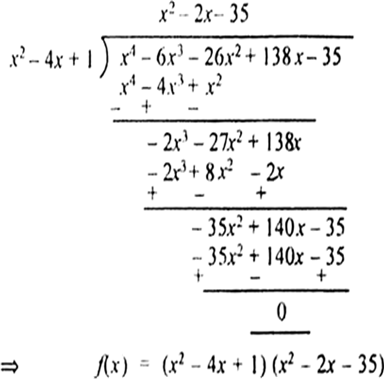
अब हम x2 – 2x – 35 के गुणनखंड प्राप्त करते है:
x2 – 2x – 35 = x2 – 7x + 5x – 35
= (x – 7) (x + 5)
अत: दिए हुए बहुपद के दो शून्यक -5 और 7 हैंl
यदि बहुपद x4 – 6x3 + 16x2 – 25x + 10 को एक अन्य बहुपद ( x2 - 2x + k ) से भाग दिया जाए और शेषफल ( x + a ) आता हो, तो ‘k’ तथा ‘a’ ज्ञात कीजिएl

क्योंकि शेषफल ( x + a ) दिया हैl
2k - 9 = 1 ⇒ 2k = 10
⇒ k = 5
तथा a = k2 - 8k + 10
अब k = 5 रखने पर, हम प्राप्त करते हैं:
a = ( 5 )2 - 8 x 5 + 10
= 25 - 40 + 10 = - 5
अत: k = 5 तथा a = - 5
यदि बहुपद (2x4 - 9x3 + 5x2 + 3x-1) के दो शून्यक हैं तो इसके सभी । शून्यक ज्ञात कीजिए।
यह दिया है कि बहुपद (2x4 - 9x3 + 5x2 + 3x-1) के दो शून्यक हैं
आइए अब f(x) को x2-4x + 1 से विभाजित करें
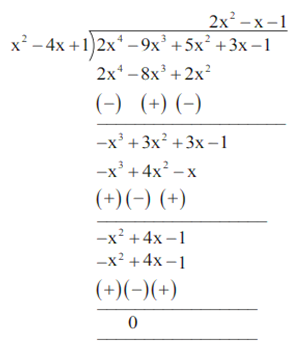
इसलिए, हमारे पास है,
f(x) = (x2- 4x + 1)(2x2-x-1)
इसलिए, f(x) के अन्य दो शून्य बहुपद 2x2-x-1 के शून्य हैं
हमारे पास
2x2-x-1 = 2x2- 2x+ x-1
= 2x (x-1) + 1(x-1)
= (2x+ 1)(x-1)
इसलिए, अन्य दो शून्य हैं - 1/2 और 1
Mock Test Series
Sponsor Area
Sponsor Area





