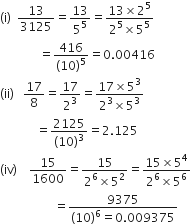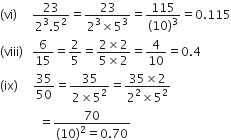गणित Chapter 1 वास्तविक संख्याएँ
Sponsor Area
NCERT Solution For Class 10 गणित गणित
निम्नलिखित संख्याओं का HCF ज्ञात करने के लिए यूक्लिड विभाजन का प्रयोग कीजिए:
(i)135 और 225 (ii) 196 और 38220 (iii) 867 और 255
अब 135 को भाज्य और 90 को भाजक मानकर दोबारा विभाजन एल्गोरिथम का प्रयोग करते हुए हम प्राप्त करते हैं:
अब 90 को भाज्य और 45 को भाजक मानकर एक बार फिर विभाजन एल्गोरिथम का प्रयोग करते हुए हम प्राप्त करते हैं:
अब शेषफल 0 प्राप्त हुआ है इसलिए हमारी प्रक्रिया समाप्त हुई
135 और 225 का HCF 45 हैl
(ii) अब 38220 को भाज्य और 196 को भाजक मानकर दोबारा विभाजन एल्गोरिथम का प्रयोग करते हुए हम प्राप्त करते हैं:
अब शेषफल 0 प्राप्त हुआ है इसलिए हमारी प्रक्रिया समाप्त हुई
इसलिए 196 और 38220 का HCF 196 हैl
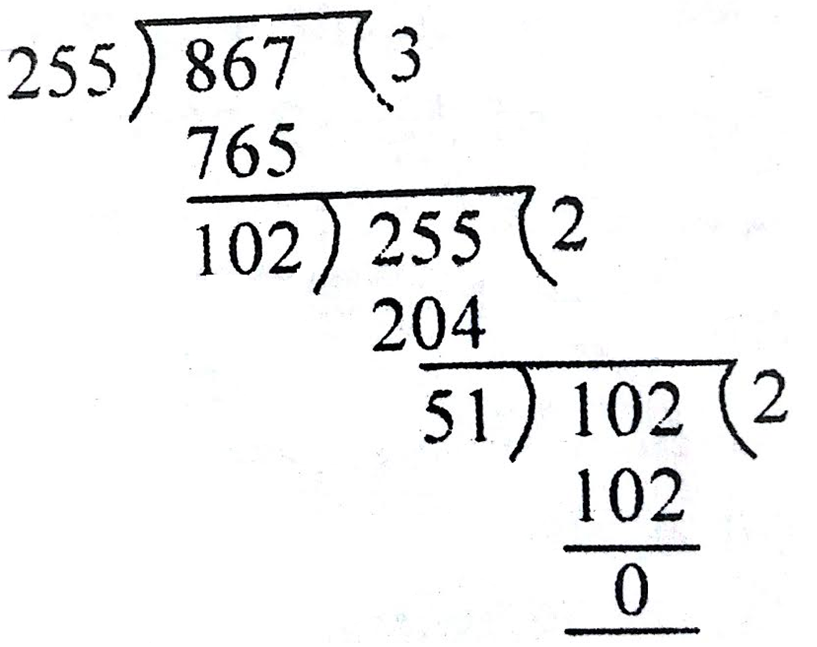
(iii) 867 = 255 x 3 + 102
255 = 102 x 2 + 51
102 = 51 x 2 + 0
अब शेष '0' रह गया है, इसलिए हमारी प्रक्रिया समाप्त हुई और
HCF (867, 255) = 51
जाँच:
दर्शाइए कि कोई भी धनात्मक विषम पूर्णांक 6q + 1 या 6q + 3 या 6q + 5 के रूप का होता है, जहाँ 'q' कोई पूर्णांक हैl
माना a कोई धनात्मक पूर्णांक है, और b = 6
माना q भागफल है और r शेषफल हैl
विभाजन अल्गोरिथम का प्रयोग करने पर
हमें प्राप्त होता है:

किसी परेड में 616 सदस्यों वाली एक सेना ( आर्मी ) की टुकड़ी को 32 सदस्यों वाले एक आर्मी बैंड के पीछे मार्च करना हैl दोनों समूहों को समान संख्या वाले स्तंभो में मार्च करना हैl उन स्तंभों की अधिकतम संख्या क्या है जिसमें वह मार्च कर सकते हैं?
सेना की टुकड़ी में सदस्यों की संख्या = 616
आर्मी बैंड में सदस्यों की संख्या = 32
32 और 616 का यूक्लिड विभाजन के साथ HCF निकलने पर
हमें प्राप्त होता है![]()
![]()
अब भागफल 0 हैl
इसलिए स्तंभों की संख्या 8 होगी
यूक्लिड विभाजन प्रमेयिका का प्रयोग करके दर्शाइए कि किसी धनात्मक पूर्णाक का वर्ग, किसी पूर्णांक m के लिए 3m या 3m + 1 के रूप का होता हैl
[ संकेत: यह मान लीजिए x कोई धनात्मक पूर्णांक हैl तब, यह 3q, 3q+ 1, या 3q + 2 के लिखा जा सकता हैl इन में से प्रत्येक का वर्ग कीजिए और दर्शाइए कि इन वर्गों को 3m या 3m + 1 के रूप में लिखा जा सकता हैl ]
माना a कोई धनात्मक पूर्णांक है, q भागफल है, r शेषफल है
तब a = bq + r जहाँ q और r भी धनात्मक पूर्णांक है और 0 ≤ r < b
b = 3, हमें प्राप्त होता है
a = 3q + r; जहाँ 0 ≤ r < 3
जब, r = 0 = ⇒ a = 3q
जब, r = 1 = ⇒ a = 3q + 1
जब, r = 2 = ⇒ a = 3q + 2
अब हम यह दर्शाएगें की धनात्मक पूर्णांक का वर्ग 3q, 3q + 1 और 3q + 2 की तरह से लिखा जा सकता है 3m or 3m + 1 किसी m पूर्णांक के लिए
⇒ 3q = (3q)2
= 9q2 = 3(3q2) = 3 m जहाँ m कोई पूर्णांक हैl
3q + 1 = (3q + 1)2
= 9q2 + 6q + 1 = 3(3q2 + 2 q) + 1
= 3m +1, जहाँ m कोई पूर्णांक हैl
3q + 2 = (3q + 2)2
= (3q + 2)2
= 9q2 + 12q + 4
= 9q2 + 12q + 3 + 1
= 3(3q2 + 4q + 1)+ 1
= 3m + 1 किसी m पूर्णांक के लिए
∴ किसी धनात्मक पूर्णांक का वर्ग या तो 3m या 3m + 1 के रूप में होता हैl
यूक्लिड विभाजन प्रमेयिका का प्रयोग करके दर्शाइए कि किसी धनात्मक पूर्णांक का घन 9m, 9m + 1 या 9m + 8 के रूप में होती हैl
माना a और b कोई दो धनात्मक पूर्णांक है जहाँ a बड़ा है b से
तब:
a = bq + r;
जहाँ q और r धनात्मक पूर्णांक है 0 ≤ r < b.
b = 3, रखने पर हमें प्राप्त होता है
a = 3q + r ; जहाँ 0 ≤ r < 3.
⇒ a के अलग-अलग मान है 3q, 3q + 1 or 3q + 2.
3q का घन 3q = (3q)3
= 27q3 = 9(3q3) = 9m ;
जहाँ m कोई पूर्णांक हैl
3q + 1 का घन 3q + 1 = (3q + 1)3
= (3q)3 + 3(3q)2 × 1 + 3(3q) × 12 + (1)3
[∵ (a + b)3 = a3 + 3a2b + 3ab2 + b3]
= 27q3 + 27q2 + 9q + 1
= 9(3q3 + 3q2 + q) + 1
= 9m + 1; जहाँ m कोई पूर्णांक हैl
3q + 2 का घन 3q + 2 = (3q + 2)3
= (3q)3 + 3(3q)2 × 2 + 3 × 3q × 22 + 23
= 27q3 + 27q2 + 36q + 8
= 9(3q3 + 3q2 + 4q) + 8 = 9m + 8; जहाँ m कोई पूर्णांक हैl
∴ किसी धनात्मक पूर्णांक का घन या तो 9m, 9m + 1 या 9m + 8 के रूप में होगाl
निम्नलिखित संख्याओं को अभाज्य गुणनखंडों के गुणनफल के रूप में व्यक्त कीजिए:
140
140 के गुणखणड होंगे
अथवा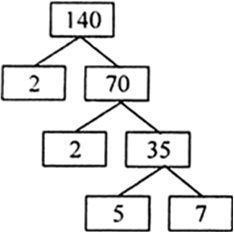
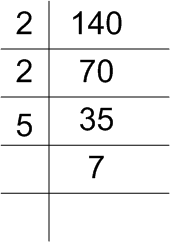
इसलिए, 140 = 2 × 2 × 5 × 7
= 22 × 5 × 7.
निम्नलिखित संख्याओं को अभाज्य गुणनखंडों के गुणनफल के रूप में व्यक्त कीजिए:
156
156 के गुणनखंड होंगे
अथवा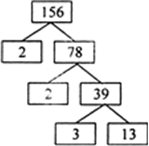

इसलिए, 156 = 2 × 2 × 3 × 13
= 22 × 3 × 13
निम्नलिखित संख्याओं को अभाज्य गुणनखंडों के गुणनफल के रूप में व्यक्त कीजिए:
3825
3825 के अभाज्य गुणनखंड होंगे
अथवा 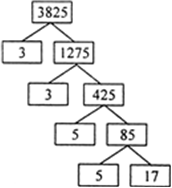

इसलिए, 3825 = 3 × 3 × × 5 × 5 × 17
= 32 × 52 × 17.
निम्नलिखित संख्याओं को अभाज्य गुणनखंडों के गुणनफल के रूप में व्यक्त कीजिए:
5005
5005 के गुणनखंड होंगे
अथवा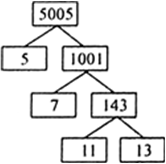

इसलिए, 5005 = 5 x 7 x 11
निम्नलिखित संख्याओं को अभाज्य गुणनखंडों के गुणनफल के रूप में व्यक्त कीजिए:
7429
अथवा
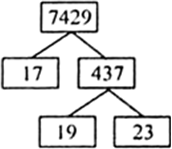

इसलिए, 7429 = 17 × 19 × 23.
पूर्णांकों ले निम्नलिखित युग्मों के HCF और LCM ज्ञात कीजिए तथा इसकी जाँच कीजिए कि दो संख्याओं का गुणनफल = HCF x LCM हैl
26 और 91
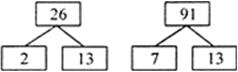
इसलिए, 26 = 2 × 13
और 91 = 7 × 13
∴ H.C.F. (26, 91) = 13
और L.C.M. (26, 91) = 2 × 7 × 13 = 182
जाँच :
L.C.M. × H.C.F. = 182 × 13 = 2366
दो संख्याओं का गुणनफल = 26 × 91 = 2366
∴ L.C.M. × H.C.F. = दो संख्याओं का गुणनफल
पूर्णांकों के निम्नलिखित यग्मों के HCF और LCM ज्ञात कीजिए तथा इसकी जाँच कीजिए कि दो संख्याओं का गुणनफल = HCF क्ष LCM होता है
510 और 92

इसलिए, 510 = 2 × 3 × 5 × 17
और 92 = 2 × 2 × 23
∴ H.C.F. (510, 92) = 2
और L.C.M. (510, 92) = 2 × 2 × 3 × 5 × 17 × 23 = 23460
जाँच :
L.C.M. × H.C.F. = 23460 × 2 = 46920
दो संख्याओं का गुणनफल = 510 × 92 = 46920
L.C.M. × H.C.F. = दो संख्याओं का गुणनफल
पूर्णांकों के निम्नलिखित यग्मों के HCF और LCM ज्ञात कीजिए तथा इसकी जाँच कीजिए कि दो संख्याओं का गुणनफल = HCF क्ष LCM होता है
336 और 54

इसलिए, 336 = 24 × 3 × 7
और 54 = 2 × 33
∴ H.C.F. = 2 × 3 = 6
L.C.M. = 24 × 33 × 7 = 3024 = 23460
जाँच:
L.C.M. × H.C.F. = 3024 × 6 = 18144
दो संख्याओं का गुणनफल = 336 × 54 = 18144
L.C.M. × H.C.F. = दो संख्याओं का गुणनफल
अभाज्य गुणनखंड विधि द्वारा निम्नलिखित पूर्णांक के HCF और LCM ज्ञात कीजिए:
12, 15 और 21
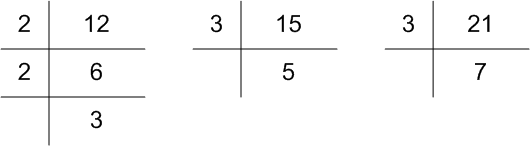
अब, 12 = 2 × 2 × 3= 22 × 3,
15 = 3 × 5, 21 = 3 × 7
यहाँ, 3 सबसे छोटा उभयनिष्ठ अभाज्य गुणनखंड हैl∴ H.C.F. (12, 15, 21) = 3
और 22, 31, 51 और 71 अभाज्य गुणनखंडों की अधिकतम घात हैंl
∴ L.C.M. (12, 15,21)= 22 × 31 × 51 × 71 =420.
अभाज्य गुणनखंड विधि द्वारा निम्नलिखित पूर्णांक के HCF और LCM ज्ञात कीजिए:
17, 23 और 29
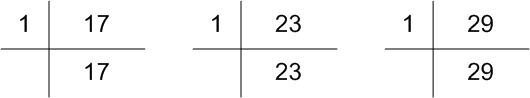
अब, 17 = 1 × 17, 23 = 1 × 23, 29 = 1 × 29
यहाँ, 1 सबसे छोटा उभयनिष्ठ हैl
∴ H.C.F. (17, 23, 29)= 1
और 171, 231 और 291 अभाज्य गुणनखंडों की अधिकतम घात हैंl
∴ L.C.M. (17, 23, 29) = 17 × 23 × 29 = 11339
अभाज्य गुणनखंड विधि द्वारा निम्नलिखित पूर्णांक के HCF और LCM ज्ञात कीजिए:
8, 9 और 25
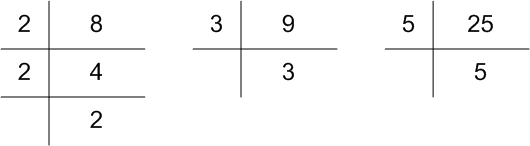
अब, 8 = 2 × 2 × 2 = 23,
9 = 3 × 3 = 32
और 25 = 5 × 5 = 52
इसलिए, यहाँ पर कोई न्यूनतम अभयनिष्ठ गुणनखंड नहीं हैl
∴ H.C.F. (8, 9, 25) = 1.
और 23, 32, और 52 अभाज्य गुणनखंड की अधिकतम घात हैl
∴ L.C.M. (8, 9, 25) = 23 × 32 × 52 = 1800
HCF (306, 657) = 9, दिया है तो LCM (306, 657) ज्ञात कीजिएl

LCM (306, 657) =
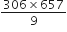
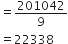
Sponsor Area
जाँच कीजिए कि क्या किसी प्राकृत संख्या के लिए संख्या 6n अंक 0 पर समाप्त हो सकती हैl
यदि 6n,  , शून्य अंक पर समाप्त होता है तो वह 5 से विभाज्य होगा अर्थात 6n के अभाज्य गुणनखंड अभाज्य संख्या 5 होगी यह सम्भव नहीं है, क्योंकि 6 के अभाज्य गुणनखंड 2 और 3 हैं और अंक गणित कि आधार भूत प्रमेय द्वारा 6n के अद्वितीय गुणनखंड इनके अतिरिक्त और गुणनखंड नहीं हो सकतेl
, शून्य अंक पर समाप्त होता है तो वह 5 से विभाज्य होगा अर्थात 6n के अभाज्य गुणनखंड अभाज्य संख्या 5 होगी यह सम्भव नहीं है, क्योंकि 6 के अभाज्य गुणनखंड 2 और 3 हैं और अंक गणित कि आधार भूत प्रमेय द्वारा 6n के अद्वितीय गुणनखंड इनके अतिरिक्त और गुणनखंड नहीं हो सकतेl
अत: 6 शून्य अंक पर समाप्त नहीं हो सकता जहाँ 
व्याख्या कीजिए कि 7 x 11 x 12 + 13 और 7 x 6 x 5 x 4 x 3 x 2 x 1 + 5 भाज्य संख्याएँ क्यों हैं?
कोई भी धनात्मक संख्या जिसके दो से ज्यादा गुणनखंड बनते है वह भाज्य संख्या होती है
7 × 11 × 13 + 13 = 13 × (7 × 11 + 1)
= 13 × 78
= 13 × 13 × 3 × 2
दी गई संख्या के दो से ज्यादा गुणनखंड है इसलिए यह एक भाज्य संख्या है
इसी तरह,
7 × 6 × 5 × 4 × 3 + 5
= 5 × (7 × 6 × 4 × 3 x 2 + 1)
= 5 × 1009
⇒ दी गई संख्या भाज्य संख्या है क्योंकि इसके दो से ज्यादा गुणनखंड बनते हैl
किसी खेल के मैदान के चारों ओर एक वृताकार पथ हैl इस मैदान का एक चक्कर लगाने में सोनिया को 18 मिनट लगते हैंl, जबकि इसी मैदान का एक चक्कर लगाने में रवि को 12 मिनट लगते हैंl मान लीजिए वह दोनों एक ही स्थान और एक ही समय पर चलना प्रारंभ करके एक ही दिशा में चलते हैंl कितने समय बाद वह पुन: प्रारंभिक स्थान पर मिलेंगे?
हम 18 और 12 का LCM ज्ञात करते हैl
हम प्राप्त करते है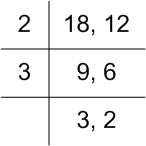
18 = 2 × 32
और 12 = 22 × 3
∴ 18 और 12 का LCM है 22 × 32 = 36.
अत: प्रांरभिक स्थान पर वे 36 मिनट बाद मिलेंगेl
सिद्ध कीजिए कि  एक अपरिमेय संख्या हैl
एक अपरिमेय संख्या हैl
 एक परिमेय संख्या हैl
एक परिमेय संख्या हैlइसलिए, हम दो पूर्णांक a तथा b (≠ 0) ज्ञात कर सकते हैं ताकि
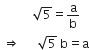
दोनों तरफ वर्ग करने पर हम प्राप्त करते है
5b2 = a2
⇒ 5, a2 को विभाजित करता हैl ......(i)
⇒ 5, a को विभाजित करता हैl ......(ii)
हम लिख सकते हैं
a = 5c जहाँ c एक पूर्णांक हैl
समीकरण (ii) में a का मान रखने पर
हम प्राप्त करते है,
5b2 = 25c2
⇒ b2 = 5c2
⇒ 5, b2 को विभाजित करता हैl
⇒ 5, b को विभाजित करता हैl ......(iii)
(ii) और (iii) से, हम देखते हैं कि a और b का 1 उभयनिष्ठ गुणनखंड हैl परन्तु यह हमारी कल्पना के विपरीत है कि a और b सह-अभाज्य हैंl अत: ![]() एक अपरिमेय संख्या हैl
एक अपरिमेय संख्या हैl
सिद्ध कीजिए कि 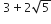 एक अपरिमेय संख्या हैl
एक अपरिमेय संख्या हैl
 एक परिमेय संख्या हैlThat is, we can find coprime a and b ( b ≠ 0 )
एक परिमेय संख्या हैlThat is, we can find coprime a and b ( b ≠ 0 )अर्थात हम सह अभाज्य ऐसी संख्याएँ a और b ( b ≠ 0 ) ज्ञात कर सकते है कि
चूँकि a और b पूर्णांक है इसलिए
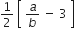 एक परिमेय संख्या है और
एक परिमेय संख्या है और  परिमेय हैl
परिमेय हैlपरन्तु इससे तथ्य का विरोधाभास प्राप्त होता है कि
 अपरिमेय संख्या हैl
अपरिमेय संख्या हैlअत: हम कह सकते है कि
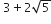 एक अपरिमेय संख्या हैl
एक अपरिमेय संख्या हैl
सिद्ध कीजिए कि निम्नलिखित संख्याएँ अपरिमेय हैं:

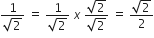 .....[ हर का प्रिमीकरण करने पर ]
.....[ हर का प्रिमीकरण करने पर ]
माना कि 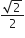 एक परिमेय संख्या हैl
एक परिमेय संख्या हैl
अब हम दी सह-अभाज्य पूर्णांक a और b (≠ 0) ज्ञात कर सकते है ताकि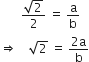
क्योंकि 'a' और 'b' पूर्णांक है,
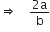 एक परिमेय संख्या हैl
एक परिमेय संख्या हैl
इसलिए 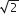 अपरिमेय है
अपरिमेय है
इसलिए हम कह सकते है कि  एक अपरिमेय है
एक अपरिमेय है
सिद्ध कीजिए कि निम्नलिखित संख्याएँ अपरिमेय हैं:

माना कि  एक परिमेय संख्या है
एक परिमेय संख्या है
अर्थात हम सह-अभाज्य पूर्णांक b (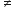 0) ज्ञात कर सकते है
0) ज्ञात कर सकते है
ताकि,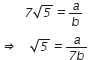
क्योंकि 'a' और 'b' पूर्णांक हैं,
 परिमेय है और इसलिए,
परिमेय है और इसलिए,  परिमेय हैl
परिमेय हैl
परन्तु इस तथ्य के विपरीत है कि  अपरिमेय हैl
अपरिमेय हैl
इसलिए  अपरिमेय हैl
अपरिमेय हैl
सिद्ध कीजिए कि निम्नलिखित संख्याएँ अपरिमेय हैं:
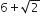
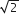 परिमेय है
परिमेय हैतब,
 परिमेय है
परिमेय हैअर्थात हम सह-अभाज्य पूर्णांक 'a' और 'b' (≠ 0)
ताकि
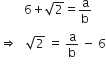
क्योंकि 'a' और 'b' पूर्णांक हैं, हम प्राप्त करते हैं
 और इसलिए,
और इसलिए, 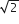 परिमेय हैl
परिमेय हैlपरन्तु यह इस तथ्य के विपरीत है कि
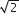 अपरिमेय हैl
अपरिमेय हैlइसलिए हम कह सकते है
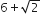 अपरिमेय हैl
अपरिमेय हैl
बिना लंबी विभाजन प्रक्रिया किए बताइए कि निम्नलिखित परिमेय संख्याओं के दशमलव प्रसार सांत है या असांत आवर्ती हैं:
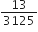
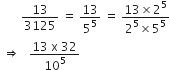
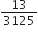 का प्रसार सांत दशमलव हैl
का प्रसार सांत दशमलव हैl
बिना लंबी विभाजन प्रक्रिया किए बताइए कि निम्नलिखित परिमेय संख्याओं के दशमलव प्रसार सांत है या असांत आवर्ती हैं:

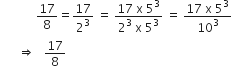
इस का प्रसार सांत दशमलव हैl
बिना लंबी विभाजन प्रक्रिया किए बताइए कि निम्नलिखित परिमेय संख्याओं के दशमलव प्रसार सांत है या असांत आवर्ती हैं:
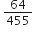
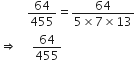
इस का प्रसार असांत आवर्ती दशमलव हैl
बिना लंबी विभाजन प्रक्रिया किए बताइए कि निम्नलिखित परिमेय संख्याओं के दशमलव प्रसार सांत है या असांत आवर्ती हैं:
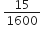
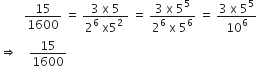
इस का प्रसार सांत दशमलव हैl
बिना लंबी विभाजन प्रक्रिया किए बताइए कि निम्नलिखित परिमेय संख्याओं के दशमलव प्रसार सांत है या असांत आवर्ती हैं:
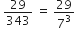
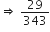 इस का प्रसार असांत आवर्ती दशमलव हैl
इस का प्रसार असांत आवर्ती दशमलव हैl
बिना लंबी विभाजन प्रक्रिया किए बताइए कि निम्नलिखित परिमेय संख्याओं के दशमलव प्रसार सांत है या असांत आवर्ती हैं: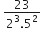
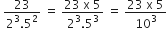
इस का प्रसार सांत दशमलव हैl
बिना लंबी विभाजन प्रक्रिया किए बताइए कि निम्नलिखित परिमेय संख्याओं के दशमलव प्रसार सांत है या असांत आवर्ती हैं: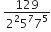
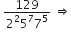 इस का प्रसार असांत आवर्ती दशमलव हैl
इस का प्रसार असांत आवर्ती दशमलव हैl
बिना लंबी विभाजन प्रक्रिया किए बताइए कि निम्नलिखित परिमेय संख्याओं के दशमलव प्रसार सांत है या असांत आवर्ती हैं:
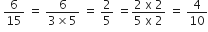 इस का प्रसार सांत दशमलव हैl
इस का प्रसार सांत दशमलव हैl
बिना लंबी विभाजन प्रक्रिया किए बताइए कि निम्नलिखित परिमेय संख्याओं के दशमलव प्रसार सांत है या असांत आवर्ती हैं:

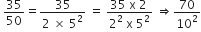
 इस का प्रसार सांत दशमलव हैl
इस का प्रसार सांत दशमलव हैl
बिना लंबी विभाजन प्रक्रिया किए बताइए कि निम्नलिखित परिमेय संख्याओं के दशमलव प्रसार सांत है या असांत आवर्ती हैं:

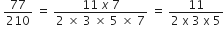
 इस का प्रसार असांत आवर्ती दशमलव हैl
इस का प्रसार असांत आवर्ती दशमलव हैl
कुछ वास्तविक संख्याओं के दशमलव प्रसार नीचे दर्शाए गए हैंl प्रत्येक स्थिति के लिए निर्धारित कीजिए कि यह संख्या है या नहींl यदि यह परिमेय संख्या है और  रूप की है तो q अभाज्य गुणनखंडो के बारे में क्या कह सकते हैं
रूप की है तो q अभाज्य गुणनखंडो के बारे में क्या कह सकते हैं
43.123456789
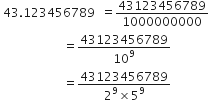
∴ 43.123456789 एक परिमेय संख्या है जो
 रूप में है जहाँ p और q सह-अभाज्य है और q के अभाज्य गुणनखंड 2n.5n के रूप में है जहाँ n एक धनात्मक पूर्णांक है
रूप में है जहाँ p और q सह-अभाज्य है और q के अभाज्य गुणनखंड 2n.5n के रूप में है जहाँ n एक धनात्मक पूर्णांक है
कुछ वास्तविक संख्याओं के दशमलव प्रसार नीचे दर्शाए गए हैंl प्रत्येक स्थिति के लिए निर्धारित कीजिए कि यह संख्या है या नहींl यदि यह परिमेय संख्या है और  रूप कि है तो q के अभाज्य गुणनखंडो के बारे में क्या कह सकते है?
रूप कि है तो q के अभाज्य गुणनखंडो के बारे में क्या कह सकते है?
0.120120012000120000 ...
कुछ वास्तविक संख्याओं के दशमलव प्रसार नीचे दर्शाए गए हैंl प्रत्येक स्थिति के लिए निर्धारित कीजिए कि यह संख्या है या नहींl यदि यह परिमेय संख्या है और  रूप कि है तो q के अभाज्य गुणनखंडो के बारे में क्या कह सकते है?
रूप कि है तो q के अभाज्य गुणनखंडो के बारे में क्या कह सकते है?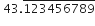
 रूप में लिखा जा सकता हैl जहाँ p और q सह-अभाज्य है तथा q के अभाज्य गुणनखंड 2n5n के रूप में हैं जहाँ n एक धनात्मक पूर्णांक हैl
रूप में लिखा जा सकता हैl जहाँ p और q सह-अभाज्य है तथा q के अभाज्य गुणनखंड 2n5n के रूप में हैं जहाँ n एक धनात्मक पूर्णांक हैl
Sponsor Area
छोटी से छोटी अभाज्य संख्या तथा छोटी से छोटी भाज्य संख्या का म.स. (HCF) क्या है?
छोटी से छोटी अभाज्य संख्या 2 है, छोटी से छोटी भाज्य संख्या 4 है|
इनका म.स. (HCF) 2 है|
दिया है कि अपरिमेय संख्या है, तो सिद्ध कीजिये कि यह एक अपरिमेय संख्या है।
मान लें कि एक परिमेय संख्या है।
इसीलिए वहां सह अभाज्य सकारात्मक पूर्णांक a और b मौजूद होंगे
यह इस तथ्य के विपरीत है कि एक अपरिमेय संख्या है
इसलिए हमारी धारणा गलत है।
अत, एक अपरिमेय संख्या है।
404 तथा 96 का म.स. (HCF) तथा ल.स. (LCM) ज्ञात कीजिए तथा निम्न का सत्यापन कीजिए : HCF XLCM = दोनों दी गई संख्याओं का गुणनफल
404 = 22× 101
96 = 25 × 3
LCM = 25 x 31 x 1011
= 25 x 31 x 1011
= 9696
संख्याओं का उत्पाद = 96x404 = 38784
इसलिए, HCF x LCM = दो संख्याओं का उत्पाद।
Mock Test Series
Sponsor Area
Sponsor Area