Mathematics Chapter 5 Introduction To Euclid's Geometry
Sponsor Area
NCERT Solution For Class 9 About 2.html
The cost of a notebook is twice the cost of a pen. Write a linear equation in two variables to represent this statement.
Let the cost of a notebook be Rs x and the cost of a pen be Rs y.
Then, according to the given condition of the question,
x = 2y
⇒ x – 2y = 0
This is the required linear equation in two variables x and y.
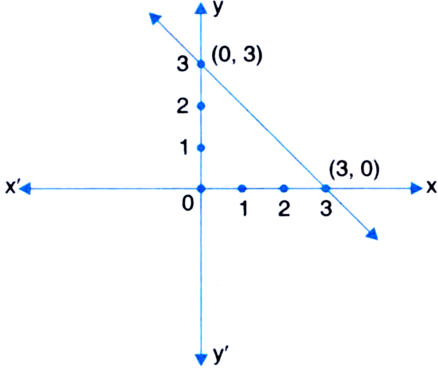
Express the following linear equations in the form ax + by + c = 0 and indicate the values of a, b and c in each case:

Comparing with ax + by + c = 0, we get
a = 2, b = 3, c =
Express the following linear equations in the form ax + by + c = 0 and indicate the values of a, b and c in each case:
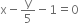
Comparing with ax + by +c = 0, we get
a = 1, b =
Express the following linear equations in the form ax + by + c = 0 and indicate the values of a, b and c in each case:
- 2x + 3y = 6
- 2x + 3y = 6![]() - 2x + 3y - 6 = 0
- 2x + 3y - 6 = 0
Comparing with ax + by + c = 0, we get
a = - 2, b = 3, c = -6
Express the following linear equations in the form ax + by + c = 0 and indicate the values of a, b and c in each case:
x = 3y
x = 3y![]() x - 3y + 0 = 0
x - 3y + 0 = 0
Comparing with ax + by + c = 0, we get
a = 1, b = -3, c = 0
Express the following linear equations in the form ax + by + c = 0 and indicate the values of a, b and c in each case:
2x = - 5y
2x = - 5y![]() 2x + 5y + 0 = 0
2x + 5y + 0 = 0
Comparing with ax + by + c = 0, we get
a = 2, b = -5, c = 0
Express the following linear equations in the form ax + by + c = 0 and indicate the values of a, b and c in each case:
3x + 2 = 0
3x + 2 = 0![]() 3x + 0y + 2 = 0
3x + 0y + 2 = 0
Comparing with ax + by + c = 0, we get
a = 3, b = 0, c = 2
Express the following linear equations in the form ax + by + c = 0 and indicate the values of a, b and c in each case:
y - 2 = 0
y - 2 = 0 ![]() 0.x + 1.y - 2 = 0
0.x + 1.y - 2 = 0
Comparing with ax + by + c = 0, we get
a = 0, b = 1, c = -2
Express the following linear equations in the form ax + by + c = 0 and indicate the values of a, b and c in each case:
5 = 2x
5 = 2x![]() -2x + 5 = 0
-2x + 5 = 0![]() -2x + 0.y + 5 = 0
-2x + 0.y + 5 = 0
Comparing with ax + by + c = o, we get a = - 2, b = 0, c = 5
Express the following statement as a linear equation in two variables by taking present ages (in years) of father and son as x and y, respectively. Age of father 5 years ago was two years more than 7 times the age of his son at that time.
Let the present ages of father and son be x years and y years respectively.
Then,
Age of father 5 years ago = (x – 5) years
Age of his son 5 years ago = (y – 5) years
According to the question,
x – 5 = 7(y – 5) + 2
⇒ x – 5 = 7y – 35 + 2
⇒ x – 7y + 28 = 0
which is the required linear equation in two variables.
Write the equation 2x = y in the form ax + by + c = 0 and find the values of a, b, c in the equation. How many solution this equation has?
The given equation is
2x = y ⇒ 2x – y
⇒ 2x – y + 0 = 0
Comparing with ax + by + c = 0, we get
a = 2
b = –1
c = 0
This equation has infinitely many solutions.
Compare the equation  = 2y – 3 and lx + my – n = 0 and write the value of l, m and n.
= 2y – 3 and lx + my – n = 0 and write the value of l, m and n.

Comparing with lx + my - n = 0, we get
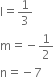
Express the linear equation 7 = 2x in the form ax + by + c = 0 and also write the values of a, b and c
7 = 2x
⇒ 2x – 7 = 0
⇒ 2x + 0y – 7 = 0
Comparing with ax + by + c = 0, we get
a = 2
b = 0
c = –7
Write each of the following equations in the form ax + by + c = 0 and indicate the values of a, b and c in each case:
(i) 2x + 3y = 4.37
(ii) x - 4 = 
(iii) 4 = 5x - 3y
(iv) 2x = y
Solution not provided.
Ans. (i) 2X + 3Y - 4.37 = 0; a = 2, b = 3 and c = - 4.37
(ii) x - ![]() - 4 = 0; s = 1, b =
- 4 = 0; s = 1, b = ![]() c = -4
c = -4
(iii) - 5x + 3y + 4 = 0; a = -5, b = 3 and c = 4
or
5x - 3y - 4 = 0; a = 5, b = 3 and c = -4
(iv) 2x - y + 0 = 0; a = 2, b = -1 and c = 0
Write each of the following as an equation in two variables:
(i) x = – 5 (ii) y = 2
(iii) 2x = 3 (iv) 5y = 2.
Solution not provided.
Ans. (i) 1 x + 0y + 5 = 0
(ii) 0x + 1y - 2 = 0
(iii) 2x + 0y - 3 = 0
(iv) 0x + 5y - 2 = 0
Which one of the following options is true, and why?
y = 3x + 5 has
(i) a unique solution,
(ii) only two solutions,
(iii) infinitely many solutions.
The true option is (iii) y = 3x + 5 has infinitely many solutions.
Reason. For every value of x, there is a corresponding value of y and vice-versa.
Write four solutions for each of the following equations:
2x + y = 7
2x +y = 7
2x + y = 7
⇒ y = 7 – 2x
Put x = 0, we get y = 7 – 2(0) = 7 – 0 = 7
Put x = 1, we gety = 7 – 2(1) = 7 – 2 = 5
Put x = 2, we get y = 7 — 2(2) = 7 – 4 = 3
Put x = 3, we get y = 7 – 2(3) = 7– 6 = 1
∴ Four solutions are (0, 7), (1, 5), (2, 3) and (3, 1).
Sponsor Area
Write four solutions for each of the following equations:
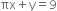
Put x = 0, we get y = 9 -
Put x = 1, we get y = 9 -
Put x =-1 we get y = 9 -
Write four solutions for each of the following equations:
x = 4y
x = 4y![]()
![]()
Put x = 0, we get y = ![]()
Put x = 4, we get y = ![]()
Put x = 4, we get y = ![]()
Put x = 2, we get y = ![]()
![]() Four solution are (0, 0) (4, 1), (-4, -1) and
Four solution are (0, 0) (4, 1), (-4, -1) and ![]()
Check which of the following are solutions of the equation x – 2y = 4 and which are not:
(0, 2)
(0, 2)
Put x = 0 and y = 2 in (i)., we get
x - 2y = 0 -2(2) = - 4, which is not 4![]() (0, 2) is not a solution of (1).
(0, 2) is not a solution of (1).
Check which of the following are solutions of the equation x – 2y = 4 and which are not:
(2, 0)
(2, 0)
Put x = 2 and y = 0 in (i)., we get
x - 2y = 2 -2(0) = 2 - 0 = 2, which is not 4![]() (2, 0) is not a solution of (1).
(2, 0) is not a solution of (1).
Check which of the following are solutions of the equation x – 2y = 4 and which are not:
(4, 0)
(4, 0)
Put x = 4 and y = 0 in (i)., we get
x - 2y = 4 -2(0) = 4, which is not 4![]() (4, 0) is a solution of (1).
(4, 0) is a solution of (1).
Check which of the following are solutions of the equation x – 2y = 4 and which are not:
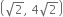
Put x =
x - 2y =
Check which of the following are solutions of the equation x – 2y = 4 and which are not:
(1, 1)
(1, 1)
Put x = 1 and y = 1 in (i), we get
x - 2y = 1 -2(1) = 1 - 2 = - 1, which is not 4.![]() (1, 1) is not a solution of (1).
(1, 1) is not a solution of (1).
Find the value of k, if x = 2, y = 1 is a solution of the equation 2x + 3y = k.
If x = 2, y = 1 is a solution of the equation 2x + 3y = k, then these values will satisfy the equation. So, putting x = 2 and y = 1 in the equation, we get
2(2) + 3(1) = k
⇒ 4 + 3 = k
⇒ k = 7.
Find at least 3 solutions for the following linear equation in two variables:
2x + 5y = 13
2x + 5y = 13![]() 5y = 13 - 2x
5y = 13 - 2x ![]()
![]()
Put x = 0, then ![]()
Put x = 1, then ![]()
Put x = 2, then ![]()
Put x = 3, then ![]()
![]() are the solutions of equation 2x + 5y = 13.
are the solutions of equation 2x + 5y = 13.
Find solutions of the form x = a, y = 0 and x = 0, y = b for the following pairs of equations. Do they have any common such solution?
3x + 2y = 6 and 5x + 2y = 10
3x + 2y = 6
Put y = 0, we get 3x + 2(0) = 6![]() 3x = 6
3x = 6![]()
![]()
![]() (0, 3) is a solution
(0, 3) is a solution
5x + 2y = 10
Put y = 0, we get 5x + 2(0) = 10![]() 5x = 10
5x = 10![]()
![]()
![]() (0, 5) is a solution.
(0, 5) is a solution.
The given equations have a common solution (2, 0)
Express x = 3y in the form ax + by + c = 0 and indicate the values of a, b and c. Write two solutions of the equation.
x = 3y![]() x - 3y = 0
x - 3y = 0![]() 1(x) + (- 3)y + (0) = 0
1(x) + (- 3)y + (0) = 0
Comparing with ax + by + c = 0, we get
a = 1
b = -3
c = 0
Now, x = 3y![]()
![]()
Put x = 0, then y = ![]()
Put x = 3, then y = ![]()
Hence, (0,0) and (3,1) are the two solutions of the equation x = 3y.
Find the value of ‘m’ if (–m, 3) is a solution of equation 4x + 9y – 3 = 0.
4x + 9y - 3 = 0, then
4(- m) + 9(3) - 3 = 0
Express y in terms of x in the equation x + 2y = 8. Find the points where the line represented by this equation cuts 4x-axis and y-axis.
This expresses y in terms of x.
This line will intersect x-axis at the point for while y = 0. So, put y = 0 in (1), we get
x + 2(0) = 8
⇒ x = 8
Hence, line (1) intersects x-axis at the point (8, 0).
5. If x = –2, y = 6 is solution of equation 3ax + 2by = 6, then find the value of b from 2(a – 1) + 2(3b – 4) = 4.
If x = –2, y = 6 is solution of equation
3ax + 2by = 6, then
3a(-2) + 2b(6) = 6![]() -6a + 12b = 6
-6a + 12b = 6![]() -a + 2b = 1 ...(1)
-a + 2b = 1 ...(1)
| dividing throughout by 6
Also
2(a - 1) + 2(3b - 4) = 4![]() 2a - 2 + 6b -8 = 4
2a - 2 + 6b -8 = 4![]() 2a + 6b = 14
2a + 6b = 14![]() a + 3b = 7 ....(2)
a + 3b = 7 ....(2)
| Dividing throughout by 2
Adding (1) and (2), we get
5b = 8 ![]() b =
b = ![]()
Putting b = ![]() in (1), we get
in (1), we get![]()
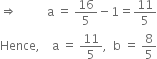
The coordinates of the points given in the following table represent some of the solutions of the equation 

Find the missing values. Also find the coordinates of the points where the line cuts x-axis and y-axis.
![]()
When x = 2, ![]()
When y = -4, -4 = ![]()
![]()
When y = 8, 8 = ![]()
![]()
![]() x = 6
x = 6
When x = -10, y = ![]()
When x = 1, y = ![]()
When y = ![]()
![]()
![]() x = -1
x = -1
Hence, the completed table is as follows:![]()
For intersection with x-axis, put y = 0
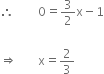
Hence, the point of intersection is ![]()
For intersection with y-axis, put x = 0![]() y = -1
y = -1
Hence, the intersection is (0, -1)
Find the coordinates of the points where the line representing the equation 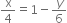 cuts the x-axis and the y-axis.
cuts the x-axis and the y-axis.
for intersection with x-axis, put y = 0
Hence the point of intersection with x-axis is (4, 0).
For intersection with y-axis, put x = 0![]()
Hence the point of intersection with y-axis is (0, 6).
Determine the point on the graph of the equation 2x + 5y = 20 where x-coordinate is 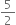 times its ordinate.
times its ordinate.
2x + 5y = 20
![]()
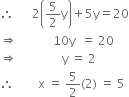
Hence the required point is (5, 2)
Find four different solutions of the equation
x + 2y = 6.
Solution not provided.
Ans. (2, 2), (0, 3), (6, 0) and (4, 1).
Find two solutions for each of the following equations:
(i) 2x – 3y = 12 (ii) 2x – 5y = 0
(iii) 3y – 4 = 0.
Solution not provided.
Ans. (i) (0, - 4) and (6, 0)
(ii) (0, 0) and ![]()
(iii) ![]()
Find the value of a so that the following equation may have x = 1, y = 1 as a solution:
3x + ay = 6
Solution not provided.
Ans. 3
Write the equation ![]() in the form of ax + by + c =0. Check whether (0, 1) and
in the form of ax + by + c =0. Check whether (0, 1) and ![]() are the solutions of the equation.
are the solutions of the equation.
Solution not provided.
Ans. ![]()
Find three different solutions for the equation 3x – 4y = –12.
Solution not provided.
Ans. (0, 3) (4, 6), (-4, 0)
Sponsor Area
Find three different solutions for the equation 6x – 8y + 32 = 0.
Solution not provided.
Ans. (0, 4) (4, 7), (8, 10)
If the point (2, –4) lies on the graph of the equation 2y = ax – 10, then find the value of a. Now express this as a linear equation in two variables.
Solution not provided.
Ans. a = 1; x - 2y - 10 = 0
Find the value of k, if x = 2, y = 1 is a solution of the equation 2x + 3y = k. Express y in terms of x and find the value of y when x = –1.
Solution not provided.
Ans. k = 7; ![]()
Write six solutions for the equation 2x + y = 7.
Solution not provided.
Ans. (0, 7), (1, 5), (2, 3), (3, 1), (4, -1), (5, - 3)
Express y in terms of x, it being given that 3x + y – 9 = 0. Check whether the points (3, 0) and (2, 2) lie on the equation.
Solution not provided.
Ans. y = 9 - 3x; Yes; No
If x = 2 and y = – 1 is a solution of the equation ax – y = 5, find the value of a, also two more solutions of the equation.
Solution not provided.
Ans. a = 2; (0, 5), (1, 7)
(2, –3) is a solution of the equation 2(x + 1) – 7(y – 2) = k, find the value of k. Find two more solutions also.
Solution not provided.
Ans. ![]()
Write the following equation in the form ax + by + c = 0 and find values of a, b and c : 4 = 3x – 5y. Check whether (1, –1) and (3, 1) are solutions of this equation or not.
Solution not provided.
Ans. 3x - 5y - 4 = 0; no; Yes
If the point (–2,4) lies on the graph of the equation (a – 1) y + 3x = 6, find four other solutions of this equation.
Solution not provided.
Ans. a = 4; (0, 2), (1, 1), (2, 0), (3, -1)
There are few families residing in a locality. For a festival some families donated र 100 each and the other families donated र 50 each. The total money collected was र 44,450. Express this in the form of an equation in two variables. Using this equation, find the number of families who donated र 100 each if the number of families donating र 50 is 111.
Solution not provided.
Ans. 2x + y = 889; 389
Check whether (3, 1), (1, 3) and (0, 8) are the solutions of the equation 3x – y = 8.
Solution not provided.
Ans. Yes; No; No
If ![]() satisfy the liner equation 3x + ky = 4
satisfy the liner equation 3x + ky = 4![]() , find the value of k, Can there be more than one value of k?
, find the value of k, Can there be more than one value of k?
Solution not provided.
Ans. K = -2; Yes
Draw the graph of each of the following linear equations in two variables:
x + y = 4
x + y = 4
x + y = 4
⇒ y = 4 – x
Table of solutions
|
X |
1 |
2 |
|
y |
3 |
2 |
We plot the points (1, 3) and (2, 2) on the graph paper and join the same by a ruler to get the line which is the graph of the equation x + y = 4.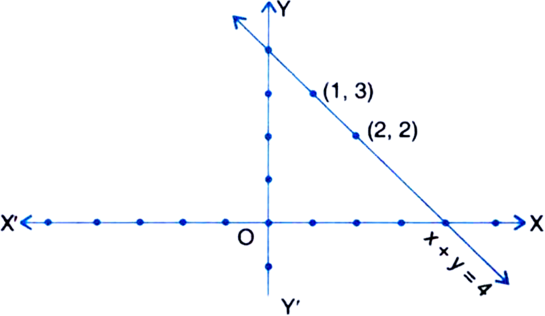
Draw the graph of each of the following linear equations in two variables:
x – y = 2
x – y = 2
x – y = 2
⇒ y = x – 2
Table of solutions
|
X |
2 |
3 |
|
y |
0 |
1 |
We plot the points (2, 0) and (3, 1) on the graph paper and join the same by a ruler to get the line which is the graph of the equation x – y = 2.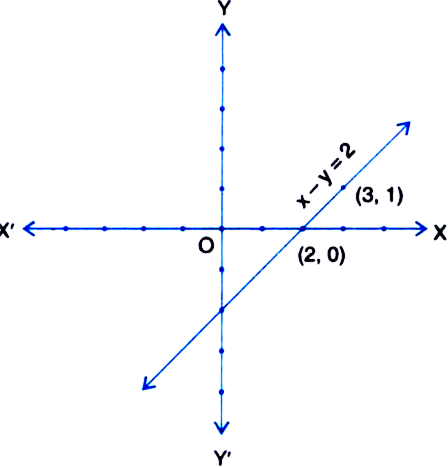
Draw the graph of each of the following linear equations in two variables:
Y = 3X
y = 3x
y =3x
Table of solutions
|
X |
0 |
1 |
|
y |
0 |
3 |
We plot the points (0, 0) and (1, 3) on the graph paper and join the same by a ruler to get the line which is the graph of the equation y = 3x.
Draw the graph of each of the following linear equations in two variables:
3 = 2x +y
3 = 2x +y
3 = 2x + y
⇒ y = 3 – 2x
Table of solutions
|
X |
1 |
0 |
|
y |
1 |
3 |
We plot the points (0, 3) and (1, 1) on the graph paper and join the same by a ruler to get the line which is the graph of the equation 3 = 2x + y.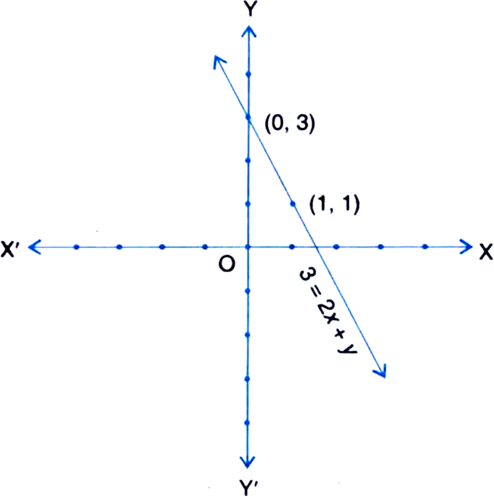
Give the equations of two lines passing through (2, 14). How many more such lines are there, and why?
The equations of two lines passing through (2, 14) can be taken as
x + y= 16
and 7x – y = 0.
There are infinitely many such lines because through a point an infinite number of lines can be drawn.
If the point (3, 4) lies on the graph of the equation 3y = ax + 7, find the value of a.
If the point (3, 4) lies on the graph of the equation
3y = ax + 7, then
3(4) = a(3) + 7![]() 12 = 3a + 7
12 = 3a + 7![]() 3a = 12 - 7
3a = 12 - 7![]() 3a = 5
3a = 5![]()
![]()
The taxi fare in a city is as follows: For the first kilometre, the fare is Rs 8 and for the subsequent distance it is Rs 5 per km. Taking the distance covered as x km and total fare as Rs y, write a linear equation for this information, and draw its graph.
Total distance covered = x km
Total fare = Rs y
Fare for the first kilometre = Rs 8
Subsequent distance = (x – 1) km
Fare for the subsequent distance = Rs 5(x – 1)
According to the question,
y = 8 + 5 (x – 1)
⇒ y = 8 + 5x – 5
⇒ y = 5x + 3
Table of solutions
|
x |
0 |
1 |
|
y |
3 |
8 |
We plot the points (0, 3) and (1, 8) on the graph paper and join the same by a ruler to get the line which is the graph of the equation y = 5x + 3.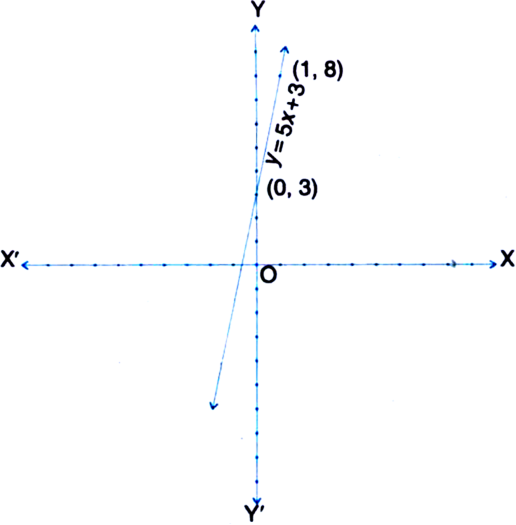
From the choices given below, choose the equation whose graphs are given in Fig. (1) and Fig. (2).
For Fig. 1 For Fig. 2
(i) y = x (i) y = x + 2
(ii) x + y = 0 (ii) y = x – 2
(iii) y = 2x (iii) y = – x + 2
(iv) 2 + 3y = 7x (iv) x + 2y = 6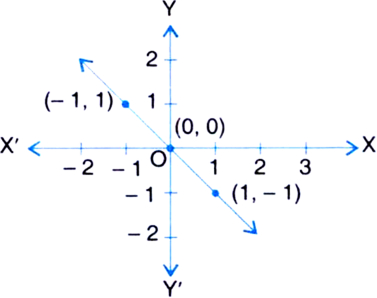
Fig. 1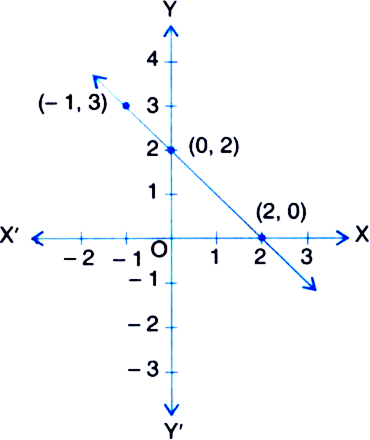
Fig. 2
For Fig. (1). The correct equation is
(ii) x + y = 0.
For Fig. (2). The correct equation is
(iii) y = – x + 2.
If the work done by a body on application of a constant force is directly proportional to the distance travelled by the body, express this in the form of an equation in two variables and draw the graph of the same by taking the constant force as 5 units. Also read from the graph the work done when the distance travelled by the body is
(i) 2 units (ii) 0 unit.
Let the work done by the constant force be y units and the distance travelled by the body be x units.
Constant force = 5 units
We know that
Work done = Force x Displacement
⇒ y = 5x
Table of solutions
|
X |
0 |
1 |
|
y |
0 |
5 |
We plot the points (0, 0) and (1, 5) on the graph paper and join the same by a ruler to get the line which is the graph of the equation y = 5x.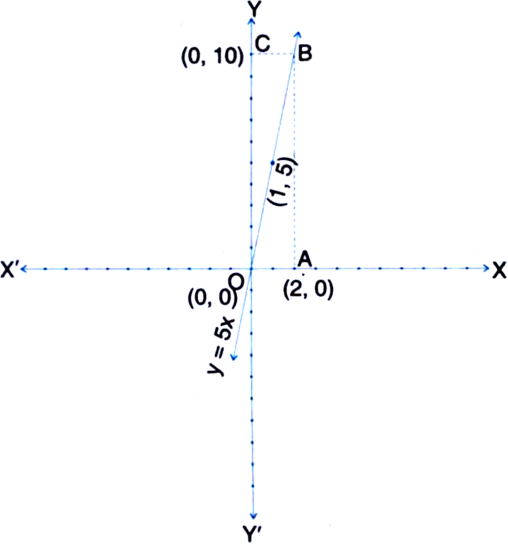
(i) Let A → (2, 0), Through A, draw a line parallel to OY to intersect the graph of the equation y = 5x at B. Through B, draw a line parallel to OX to intersect OY at C. Then,
C → (0, 10)
∴ Work done when the distance travelled by the body is 2 units = 10 units.
(ii) Clearly y = 0 when x = 0. So, the work done when the distance travelled by the body is 0 units is 0 units.
Yamini and Fatima, two students of Class IX of a school, together contributed Rs 100 towards the Prime Minister’s Relief Fund to help the earthquake victims. Write a linear equation which satisfies this data. (You may take their contributions as Rs x and Rs y.) Draw the graph of the same.
Let the contributions of Yamini and Fatima be Rs x and Rs y respectively.
Then according to the question
x + y = 100
This is the linear equation which the given data satisfies.
Now, x + y = 100
⇒ y = 100 – x
Table of solutions
|
X |
0 |
50 |
|
y |
100 |
50 |
We plot the points (0, 100) and (50, 50) on the graph paper and join the same by a ruler to get the line which is the graph of the equation x + y = 100.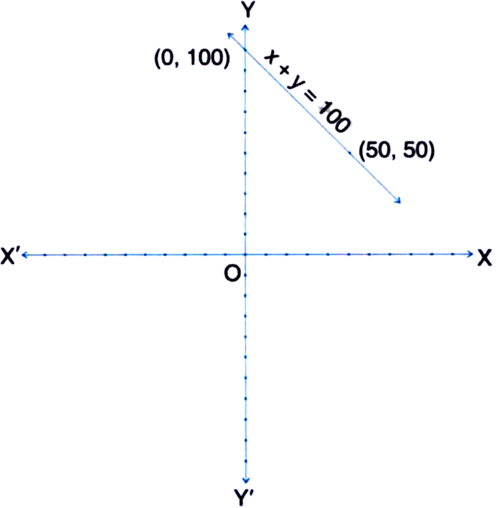
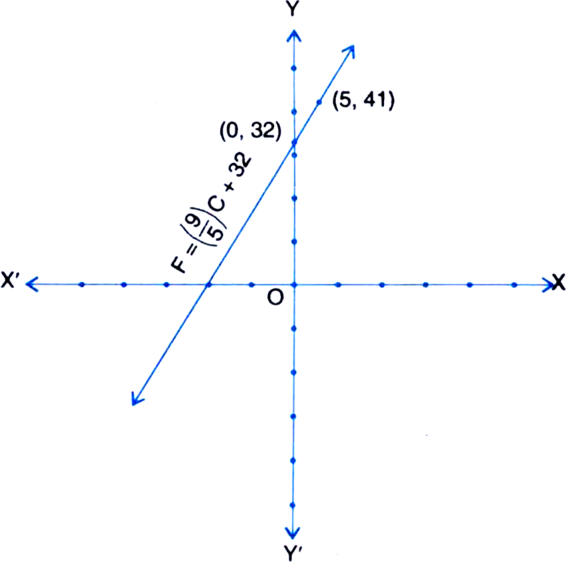
In countries like USA and Canada, temperature is measured in Fahrenheit, whereas in countries like India, it is measured in Celsius. Here is a linear equation that converts Fahrenheit to Celsius:

Draw the graph of the linear equation above using Celsius for x-axis and Fahrenheit for y-axis.
Table of solutions
|
c |
0 |
5 |
|
F |
32 |
41 |
We plot the points (0, 32) and (5, 41) on the graph paper and join the same by a ruler to get the line which is the graph of the equation
In countries like USA and Canada, temperature is measured in Fahrenheit, whereas in countries like India, it is measured in Celsius. Here is a linear equation that converts Fahrenheit to Celsius:

If the temperature is 30°C, what is the temperature in Fahrenheit?
When C = 30, then F =
= 54 + 32
= 86
In countries like USA and Canada, temperature is measured in Fahrenheit, whereas in countries like India, it is measured in Celsius. Here is a linear equation that converts Fahrenheit to Celsius:

If the temperature is 95°F, what is the temperature in Celsius?
When F = 95, then
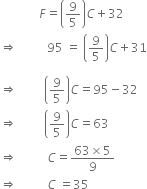
![]() Required temperature = 350C
Required temperature = 350C
In countries like USA and Canada, temperature is measured in Fahrenheit, whereas in countries like India, it is measured in Celsius. Here is a linear equation that converts Fahrenheit to Celsius:

If the temperature is 95°F, what is the temperature in Celsius?
When C = 0, Then ![]()
![]() Required temperature = 320F
Required temperature = 320F
When F = 0, then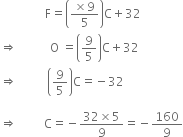
![]() Required temperature =
Required temperature = ![]()
In countries like USA and Canada, temperature is measured in Fahrenheit, whereas in countries like India, it is measured in Celsius. Here is a linear equation that converts Fahrenheit to Celsius:

Is there a temperature which is numerically the same in both Fahrenheit and Celsius? If yes, find it.
When C = 0, then]
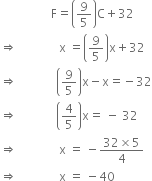
![]() Numerical value of required temperature = -40.
Numerical value of required temperature = -40.
Draw the graph of the equation 3x + y = 8. Use it to find some solutions of the equation and check from the graph whether x = 2, y = 2 is a solution.
3x + y = 8
⇒ y = 8 – 3x
Table of solutions
|
x |
0 |
3 |
|
y |
8 |
-1 |
We plot the points (0, 8) and (3, – 1) on the graph paper and join the same by a ruler to get the line which is the graph of the equation 3jc + y = 8.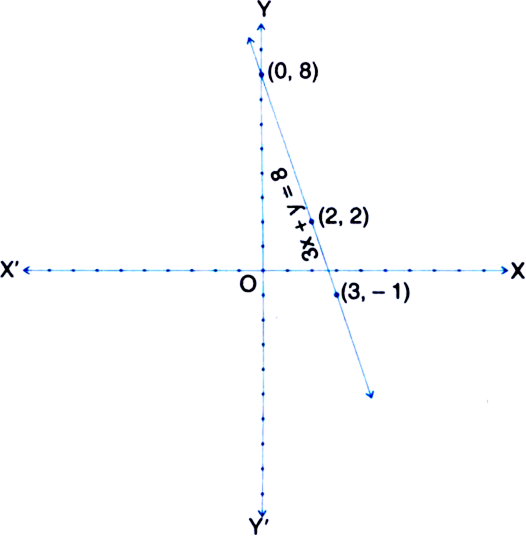
∵ The point (2, 2) lies on the graph.
∴ x = 2, y = 2 is a solution of the given equation.
Force applied on a body is directly proportional to the acceleration produced in the body. Write an equation to express the situation and plot the graph of the equation taking constant to be 5 units.
Let the force applied on a body be y units and the acceleration produced in the body be x units. Then,
y ∝ x
⇒ y = kx
Here, k = 5 units |Given
∴ y = 5x ...(1)
(1) is an equation to express the situation. Table of solutions
|
X |
0 |
1 |
|
y |
0 |
5 |
We plot the points (0, 0) and (1, 5) on a graph paper and join the same by a ruler to get the line which is the graph of the equation y = 5x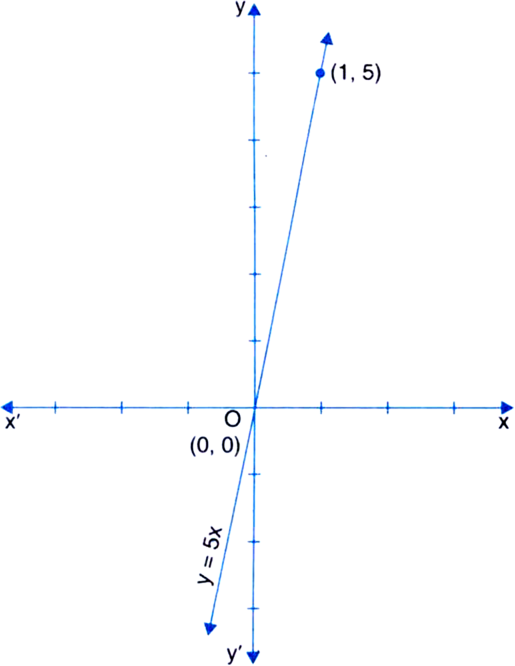
Shade the triangle formed by the graphs of 2x – y = 4, x + y = 2 and the y-axis. Write the coordinates of vertices of the triangle.
2x – y = 4
⇒ y = 2x – 4
Table of solutions
|
X |
2 |
3 |
|
y |
0 |
2 |
We plot the points (2, 0) and (3, 2) on a graph paper and join the same by a ruler to get the line which is the graph of the equation 2x – y = 4
x + y = 2
⇒ y = 2 – x
Table of solutions
|
X |
2 |
0 |
|
y |
0 |
2 |
We plot the points (2, 0) and (0, 2) on the same graph paper and join the same by a ruler to get the line which is the graph of the equation x + y = 2.
From graph, we see that the coordinates of the vertices of the triangle are (2, 0), (0, 2) and (0, –4). The triangle has been shaded.
Give the equations of two lines passing through (1, 2). How many more such lines are there and why?
Two lines passing through (1, 2) are
x + y = 3 ...(1)
and y = 2x ...(2)
Infinitely many more such lines can be found because the general equation of a line is ax + by + c = 0. For a given point (x, y) through which the line passes and for an arbitrary pair of values of a and b, c can be determined so as to satisfy ax + by + c = 0. This holds good for each given point and each arbitrary pair of values of a and b. Hence, infinitely many lines can be found passing through a given point.
Find three different solutions of the equation: 4x + 3y = 12, from its graph.
The given equation is
4x + 3y = 12
![]() 3y = 12 - 4x
3y = 12 - 4x![]()
![]()
Table of solutions
|
X |
3 |
0 |
|
y |
0 |
4 |
We plot the points (3, 0) and (0, 4) on a graph paper and join the same by a ruler to get the line which is the graph of the equation 4x + 3y = 12.
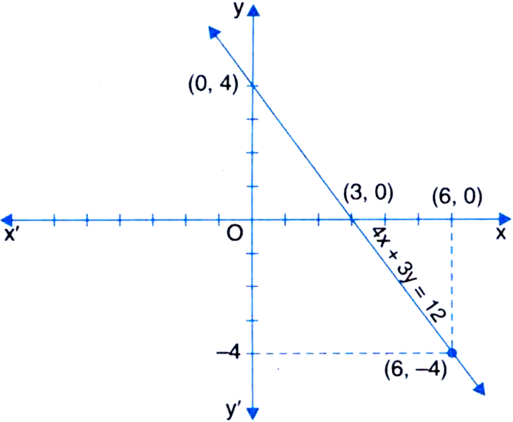
Three different solutions of the equation 4x + 3y = 12 from the graph are (0, 4), (3, 0) and (6, –4).
Draw the graph of x + y = 3 and 2x + 2y = 8 on the same axes. What does the graph of these lines represent?
x + y = 3 ...(1)
⇒ y = 3 – x
Table of solutions
|
X |
0 |
3 |
|
y |
3 |
0 |
We plot the points (0, 3) and (3, 0) on a graph paper and join these points by a ruler to get the line which is the graph of the equation x + y = 3.
Table of solutions
|
X |
0 |
4 |
|
y |
4 |
0 |
We plot the points (0, 4) and (4, 0) on the same graph paper and join these points by a ruler to get the line which is the graph of the equation 2x + 2y = 8.
From graph, we see that the lines represented by the equations (1) and (2) are parallel.
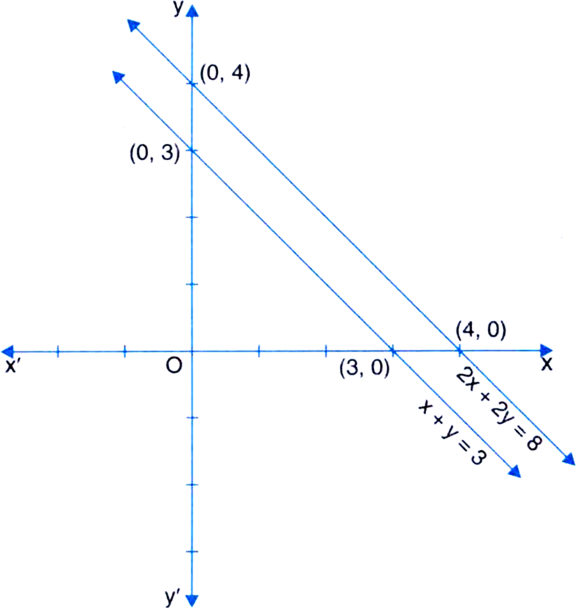
Draw graph of the following linear equations on the same axes
(i) x + y = 3
(ii) 3x – 2y = 4
Also shade the region formed by their graphs and y-axis.
(i) x + y = 3 ...(1)
⇒ y = 3 – x
Table of solutions
|
X |
0 |
3 |
|
y |
3 |
0 |
We plot the points (0, 3) and (3, 0) on a graph paper and join the same by a ruler to get the line, which is the graph of the equation x + y = 3.
(ii) 3x - 2y = 4 ....(2)![]() 2y = 3x - 4
2y = 3x - 4![]()
Table of solutions
|
X |
2 |
4 |
|
y |
1 |
4 |
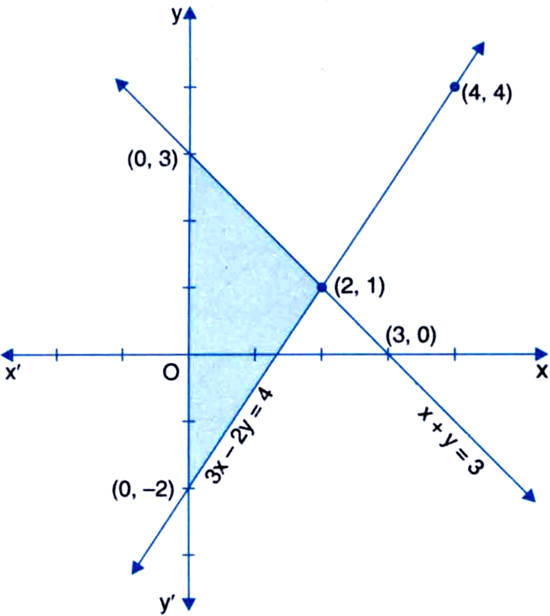
We plot the points (2, 1) and (4, 4) on the same graph paper on the same axes and join the same by a ruler to get the line which is the graph of the equation 3x – 2y = 4.
The region formed by the graphs of the given linear equations and y-axis has been shaded.
If x is the number of hours a labourer is on work and y his wages in rupees then y = 4x + 3. Draw the work wages graph of this equation. From the graph, find the wages of a labourer who puts in 4 hours of work.
We have
y = 4x + 3 Table of solutions
|
X |
0 |
1 |
|
y |
3 |
7 |
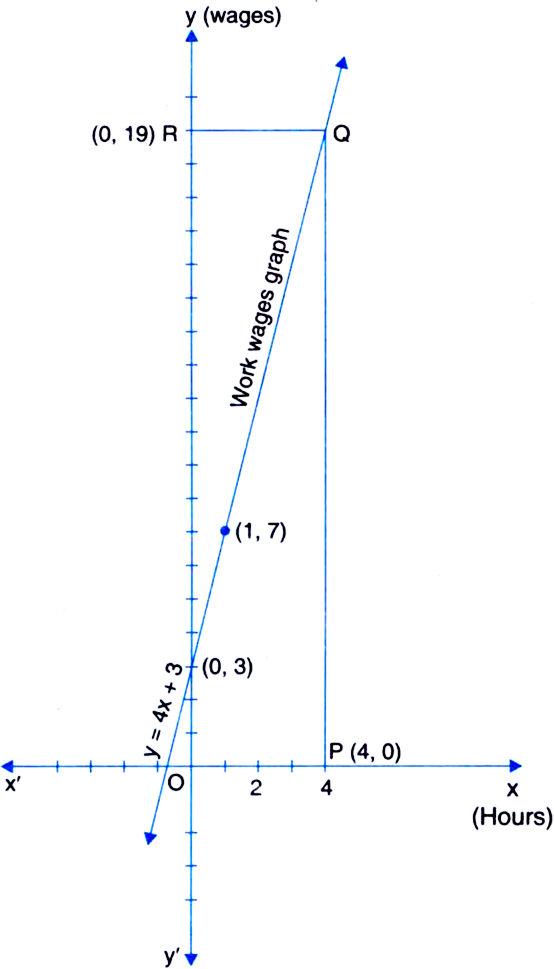
We plot the points (0, 3) and (1, 7) on a graph paper and join the same by a ruler to get the line, which is the graph of the equation y = 4 x + 3.
This gives the work wages graph of the given equation.
Now, on x-axis, take a point P(4, 0). From P draw a line parallel to y-axis intersecting the work wage graph at Q. From Q, draw a line parallel to x-axis to intersect the y-axis at R. We see that R is (0,19).Hence, the wages of a labourer who puts in 4 hours of work is र 19.
Draw the graph of the linear equation  Check from the graph that (7, 5) is a solution of the linear equation.
Check from the graph that (7, 5) is a solution of the linear equation.
Table of solutions
|
x |
1 |
4 |
|
y |
1 |
3 |
We plot the points (1,1) and (4, 3) on a graph paper and join the same by a ruler to get the line which is the graph of the equation ![]()
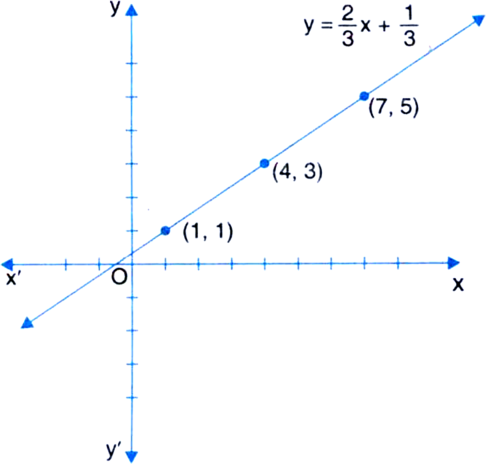
From graph, we see that the point (7, 5) lies on the graph, so it is a solution of the linear equation.
Draw the graph of linear equation 2x + y = 8on Cartesian plane. Write the coordinates of the points where this line intersects x-axis and y-axis.
2x + y = 8
⇒ y = 8 – 2x
Table of solutions
|
x |
4 |
0 |
|
y |
0 |
8 |
We plot the points (4, 0) and (0, 8) on a graph paper and join the same by a ruler to get the line which is the graph of the equation 2x + y = 8.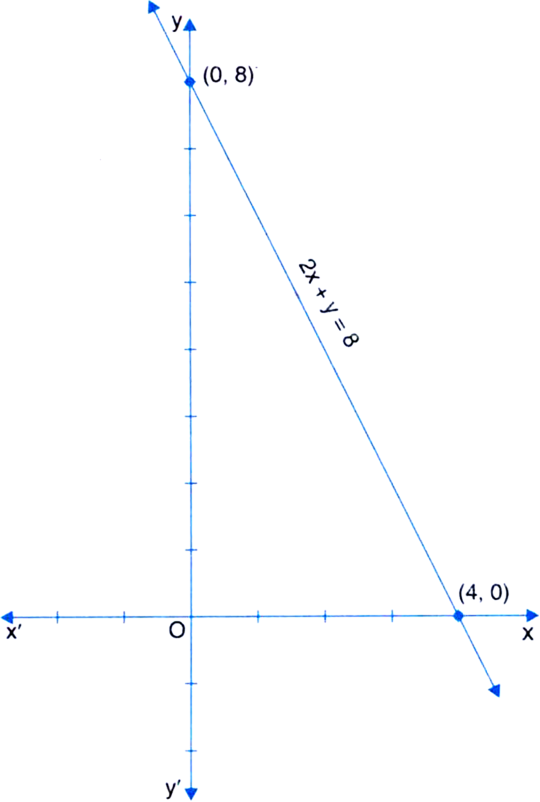
From graph, we see that this line intersects the x-axis at the point (4, 0) and the y-axis at the point (0, 8).
Rohit is driving his car at a uniform speed of 80 km per hour. Draw time-distance graph taking time along x-axis and distance along y-axis.
Let us represent time (in hour) by x and distance (in km) by y. Then, we have y = 80 x
Table of solutions
|
X |
1 |
2 |
3 |
4 |
|
y, |
80 |
160 |
240 |
320 |
We plot the points (1, 80). (2, 160), (3, 240) and (4,320) on a graph paper and join these points by a ruler to get the line which is the graph of the equation
y = 80x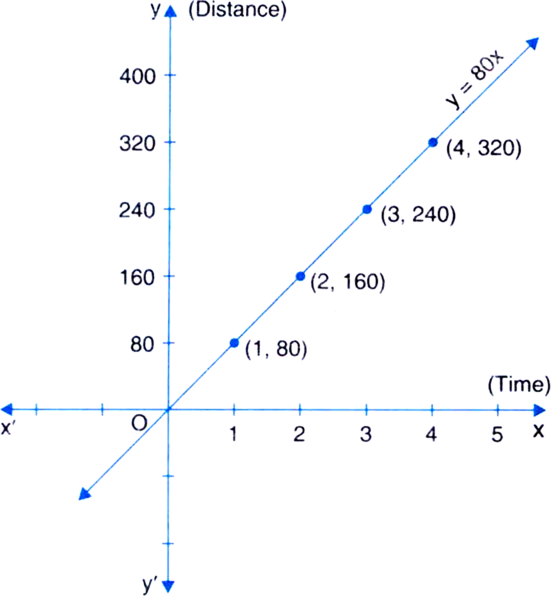
A part of family budget on milk is constant and is fixed at र 500, while the other is variable and it depends on the need for milk at the rate oft 20 per litre. If extra milk taken is x litre and total expenditure on milk is रy, then write a linear equation for this problem. Draw its graph.
According to the question, the linear equation for the given problem is
⇒ y = 500 + 20x ...(1)
Table of solutions
|
X |
0 |
5 |
|
y |
500 |
600 |
We plot the points (0, 500) and (5, 600) on a graph paper and join the same by a ruler to get the line which is the graph of the equation (1).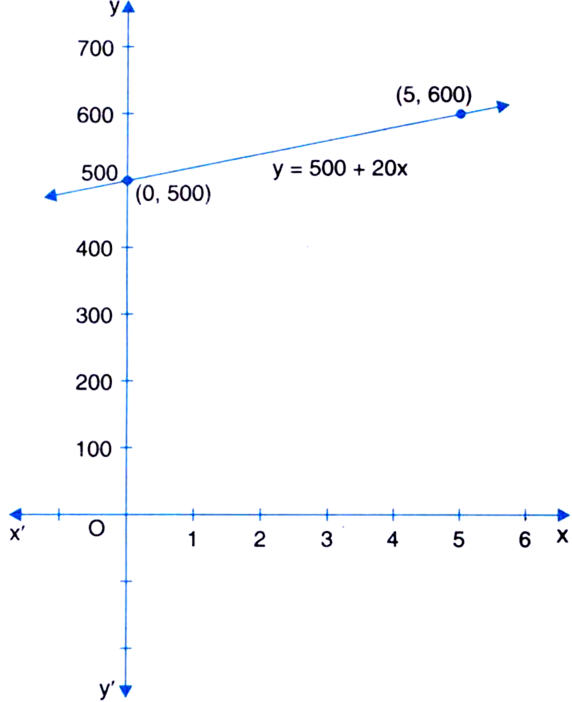
Draw the graph of linear equation 4x + 3y = 36. From the graph, find the value of y when x = 3 and value of x when y = 6.
4x + 3y = 36 ....(1)![]() 3y = 36 - 4x
3y = 36 - 4x![]()
![]()
Table of solutions
|
X |
0 |
9 |
|
y |
12 |
0 |
We plot the points (0, 12) and (9,0) on a graph paper and join the same by a ruler to get the line which is the graph of the equation (1).
Mark a point P(3, 0) on x-axis. From P draw PQ || y-axis to intersect the graph at Q. From Q, draw QR || x-axis to intersect the y-axis at R(0, 8).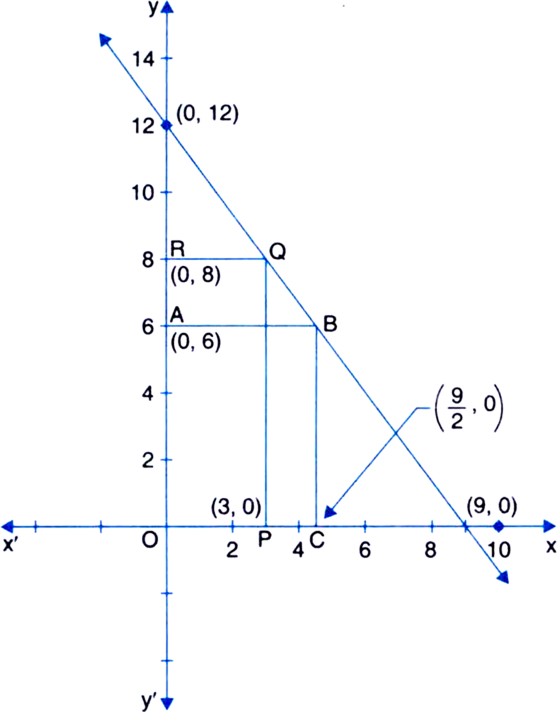
Hence, y = 8 when x = 3.
Again, mark a point A(0, 6) on y-axis. From A draw AB II x-axis to intersect the graph at B. From B, draw BC || y-axis to intersect x-axis at ![]() .
.
Hence ![]() when y = 6
when y = 6
Sponsor Area
Draw the graph of the equations x = 3 and 4x = 3y in the same graph. Find the area of the triangle formed by these two lines and the x-axis.
4x = 3y
Table of solutions
|
x |
0 |
3 |
|
y |
0 |
4 |
We plot the points (0, 0) and (3, 4) on a graph paper and join the same by a ruler to get the line which is the graph of the equation 4x = 3y.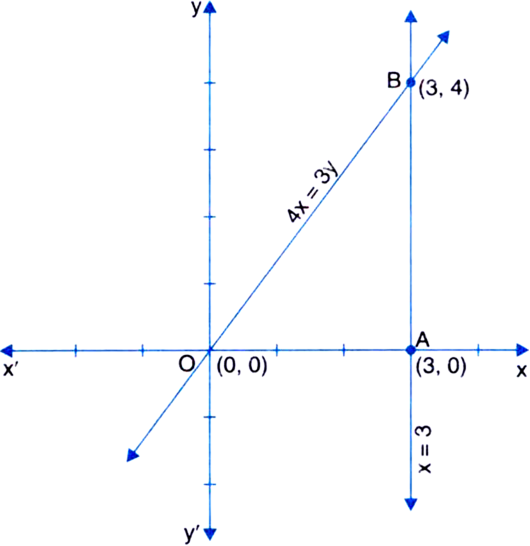
Draw the graph of the equation 2x + 3y = –5 and x + y = –1 in the same graph. Find the co-ordinates of the point of intersection of the two lines.
2x + 3y = -5![]() 3y = - 5 - 2x
3y = - 5 - 2x![]()
![]()
Table of solutions
|
X |
–1 |
2 |
|
y |
–1 |
–3 |
We plot the points (–1, –1) and (1, –3) on a graph paper and join the same by a ruler to get the line which is the graph of the equation 2x + 3y = –5.
x + y = –1
⇒ y = – 1 – x
Table of solutions
|
X |
0 |
1 |
|
y |
–1 |
–2 |
We plot the points (0, –1) and (1, –2) on the same graph paper and join the same by a ruler to get the line which is the graph of the equation x + y = –1.
From graph, we see that the coordinates of the point of intersection of the two lines are (2, –3).
Given the point (1,2), can you give the equation of a line on which it lies? How many such equations are there?
Solution not provided.
Ans. x + y = 3, y – x = 1, y = 2x, etc.; Infinitely many.
You know that the force applied on a body is directly proportional to the acceleration produced in the body. Write an equation to express this situation and plot the graph of the equation.
Solution not provided.
Ans. y = kx where k is a constant.
The following linear equation converts Fahrenheit temperature to Celcius  .
.
(i) If the temperature is 40°C, what is the temperature in Fahrenheit?
(ii) If the temperature is 95°F, what is the temperature in Celcius?
(iii) Is there a temperature which is numerically of same value in Fahrenheit and Celcius? If yes, find the temperature?
Solution not provided.
Ans. (i) 104°F (ii) 35°C (iii) –40°
Taxi fare in a city is र 8.00 for first kilometer and for the subsequent distance it is र 5.00 per km. Write a linear equation to represent this information in two variables taking distance covered as ‘x’ km and total fare as y (in र) and draw its graph. Find the distance travelled by a person if he spent र 63.00.
Solution not provided.
Ans. y = 8 + 5(x – 1) ⇒ y = 5x + 3; र 318
Find the value of ‘m’ if x = 2, y = 1 is a solution of the equation 2x + 3y = m and represent it graphically.
Solution not provided.
Ans. m = 7
Given the point (1,2), find the equation of a line on which it lies. How many such equations are there? Write the equation in the form ax + by + c = 0.
Solution not provided.
Ans. x + y = 3; infinitely many;x + y – 3 = 0m = 7
Draw the graph of linear equation 5y = 3x + 18 on Cartesian plane. From the graph check whether (–2,4) is the solution of linear equation or not.
Solution not provided.
Ans. No
Give the equation of two lines passing through (3,4). How many more such lines are there and why?
Solution not provided.
Ans. x + y = 7; y = x + 1; infinitely many
Draw the graph of the linear equation 3x + 2y = 12. Also find the points where this graph cuts x-axis and y-axis.
Solution not provided.
Ans. (4,0); (0,6)
The taxi fare in a city is as follows: for the first kilometer, the fare is र 10 and for the subsequent distance it is र 6 per km. Taking the distance covered as x km and total fare as र y, write a linear equation for this information, and draw its graph.
Solution not provided.
Ans. y = 10 + 6(x – 1) ⇒ y = 4 + 6x
Two friends Sita and Gita, together contributed र 200 tow ards Prime Minister’s Relief Fund. Write a linear equation which satisfies this data. Draw the graph.
Solution not provided.
Ans. x + y = 200 15. (i)1 (ii) 1
The cost of a note book is thrice the cost of a pen. Write a linear equation in two variables to represent this statement. Express it graphically.
Solution not provided.
Ans. y = 3x 17. (i) –4 (ii) 3
Express x in terms of y, it is being given that 7x – 3y = 15. Check if the line represented by the equation intersects the y-axis at y = –5.
Solution not provided.
Ans. ![]()
Graphically show the position of the equations x = 5 and y = –3. Name the type of quadrilateral formed with these lines and the two axes. Write the coordinates of its vertioes.
Solution not provided.
Ans. Rectangle; (0, 0), (5, 0), (5, –3), (0, –3)
Draw the graph of the linear equation y = mx + c for m = 2 and c = 1. Read from the graph the value of y when 
Solution not provided.
Ans. 4
Sketch the graph of the equation 3x + 5y = 15. Find the area of the figure formed by this line and the two axes.
Solution not provided.
Ans. ![]() square units.
square units.
Draw the graph of the linear equation 3x – y = 4. From your graph, find the values of h and k if the graph passes through the points (h, –4) and (3, k).
Solution not provided.
Ans. h = 0, k = 5
The parking charges of acaron New Delhi Railway Station for first two hours is र 50/- and र 10/- for subsequent hours. Write down an equation and draw the graph of this data. Read the charges from the graph:
(i) for one hour
(ii) for three hours
(iii) for six hours.
Solution not provided.
Ans. y = 50 + 10(x – 2) where x > 2
⇒ y = 30 + 10x where x > 2
(i) र 50 (ii) र 60 (iii) र 90
Give the geometric representations of y = 3 as an equation
in one variable
In one variable
The representation of y = 3 on the number line is as shown below:![]()
Give the geometric representations of y = 3 as an equation
in two variables.
In two variables
y = 3
⇒ 0.x + 1.y = 3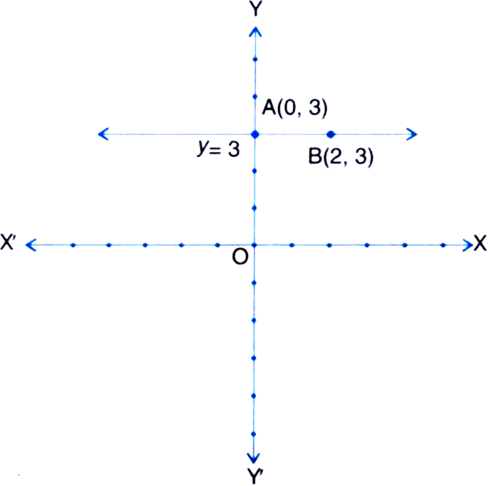
It is a linear equation in two variables x and y. This is represented by a line. All the values of x are permissible because O.x is always 0. However, y must satisfy the relation y = 3. Hence, two solutions of the given equation are x = 0, y = 3 and x = 2, y = 3.
Thus the graph AB is a line parallel to the x-axis at a distance of 3 units above it.
Give the geometric representations of 2x + 9 = 0 as an equation
in one variable
The given equation is
2x + 9 = 0
In one variable
2x + 9 = 0
⇒ 2x = – 9![]()
The representation of 2x + 9 = 0 on the number line is as shown below:

Give the geometric representations of 2x + 9 = 0 as an equation
in two variables.
In two variables
2x + 9 = 0
⇒ 2x + Oy + 9 = 0
It is a linear equation in two variables x and y. This is represented by a line. All the values of y are permissible because Oy is always 0. However, x must satisfy the relation
2x + 9 = 0, i.e. ![]() Hence, two solutions of the given equation are Hence,
Hence, two solutions of the given equation are Hence,![]()
The graph AB is a line parallel to the y-axis and at a distance of ![]() units to the left of origin O.
units to the left of origin O.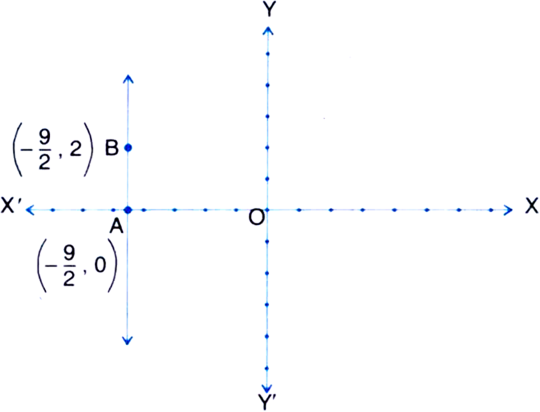
Solve for ![]() . What will be the graph of this equation?
. What will be the graph of this equation?
Solution not provided.
Ans. x = 1 5. x = 4
Solve the equation 3(x + 2) = 2(2x – 1) and represent the solution:
(i) on the number line
(ii) in the Cartesian plane.
Solution not provided.
Ans. x = 3
Give the geometrical representation of 3(x – 6) = 2x – 7 as an equation (i) in one variable (ii) in two variables.
Solution not provided.
Give the geometrical representation of 3(x – 6) = 2x – 7 as an equation (i) in one variable (ii) in two variables.
Solution not provided.
Solve 4x – 7 = 9. Represent the solution (i) on the number line
(ii) in the Cartesian plane.
Solution not provided.
Give the geometric interpretation of 7x + 6 = 2x – 4 as an equation:
(i) in one variable
(ii) in two variables.
Solution not provided.
Give the geometrical representation of the equation 3x + 15 = 0 as an equation:
(i) in one variable
(ii) in two variables
Solution not provided.
Solve 5x – 2 = 3x – 8 and represent the solution.
(i) on a number line
(ii) in the Cartesian plane.
Solution not provided.
Solve the equation 3x + 4 = 7 + 2x for x and represent the solution
(i) On a number line
(ii) In the Cartesian plane
Solution not provided.
The standard form of a linear equation in two variables x and y is
-
ax + by + c = 0
-
ax = c
-
by = c
-
x + y + c = 0
by = c
A.
ax + by + c = 0
Write a, b, c for the equation 2y –x = 7
-
–1, 2, –7
-
1,2,7
-
–1, –2, –7
-
–1, –2, –7
A.
–1, 2, –7
The equation 3x + 4y = 12 has
-
a unique solution
-
no solution
-
two solutions
-
infinitely many solutions
D.
infinitely many solutions
A linear equation in two variable., has
-
a unique solution
-
no solution
-
two solutions
-
infinitely many solutions
D.
infinitely many solutionsSponsor Area
The line y = mx + c
-
passes through origin
-
does not pass through origin
-
is parallel to x-axis
-
is parallel to y-axis
B.
does not pass through originWhere does the line 2x + 3y = 6 cut x-axis?
- at (3, 0)
- at (0, 3)
- at (0, 0)
- at (3, 3)
A.
at (3, 0)
Mow many linear equations in x and y can be satisfied by x = 1 and y = 2?
-
only one
-
two
-
infinitely many
-
three
C.
infinitely many
The graph of y = 6 is a line:
-
parallel to x-axis at a distance 6 units from the origin
-
parallel to y-axis at a distance 6 units from the origin
-
passing through the point (6, 0)
-
passing through the origin
A.
parallel to x-axis at a distance 6 units from the origin
The linear equation 2x + 5y = 7 has:
-
a unique solution
-
two solutions
-
three solutions
-
infinitely many solutions
D.
infinitely many solutions
Equation of a line passing through origin is:
-
x + y = 1
-
x = 2y – 4
-
x + y = 0
-
y = x – 1
C.
x + y = 0
x = 4 is a line:
-
parallel to y = –4
-
parallel to x-axis
-
passing through origin
-
parallel to x = –4
D.
parallel to x = –4
Solution to the equation 
-
lie on the x-axis
-
in the 3rd quadrant
-
in the 4th quadrant
-
on the y-axis
D.
on the y-axis
The equation 2x = 3 in two variables is of the form:
-
2 . x + 3 . y = 0
-
2 . x + 0 . y = 3
-
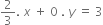
-
1 . x + 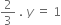
2 . x + 3 . y = 0
2 . x + 0 . y = 3
1 . x + ![]()
B.
2 . x + 0 . y = 3
To which linear equation does the graph represent?
-
3x -7y = 10
-
y - 2x = 3
-
8y - 6x = 4
-
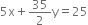
3x -7y = 10
y - 2x = 3
8y - 6x = 4
C.
8y - 6x = 4
The general form of a linear, equation in two variables is:
-
ax + by + c = 0, where a, b, c are real numbers and a, b ≠ 0
-
ax + b = 0 where a, b are real numbers and a ≠ b
-
ax2 + bx + c = 0, where a, b, c are real numbers and a, b ≠ 0
-
none of these
ax + b = 0 where a, b are real numbers and a ≠ b
A.
ax + by + c = 0, where a, b, c are real numbers and a, b ≠ 0
The graph y = mx is a:
-
straight line parallel to x-axis
-
straight line parallel to y-axis
-
line that passes through the origin
-
line that coincides with the x-axis
C.
line that passes through the originGive the equations of any three lines passing through the point (2, –3).
Solution not provided.
Ans. x + y + 1 = 0; 2x + y = 1; 3x + y = 3
Write 3 different solutions of 2x +y = .
Solution not provided.
Ans. (0, 0) (1, - 2), (2, -4)
The Auto fare in a city is as follows. For the first kilometer the fare is र 5 and for the successive distance it is र 1 per kilometer. Taking a distance covered as x kilometer and total fare as र y, write a linear equation for the above said data and draw its graph.
Solution not provided.
Ans. y = 5 + 2(x -1) ![]() y = 3 + 2x
y = 3 + 2x
Consider the point A(–2, 3)
(i) How many lines can be drawn passing through A?
(ii) Give equation of any two lines passing through A.
(iii) Without actually drawing the graph, find a point, other than A, on each of these two lines.
Solution not provided.
Ans. (i) infinitely many (ii) x +y + 1 = 0, -x + y = 5
(iii) (0, 1), (0, 5)
Draw the graphs of y = x and y = –x in the same axes. Also, find the co-ordinates of the point where the two lines intersect.
Solution not provided.
Ans. (0, 0)
Draw the graph of 3x + y = 6. At what points, does the graph intersect the axes?
Solution not provided.
Ans. (2, 0), (0, 6)
Let y vary directly as x. If y = 12 when x = 4, then write a linear equation. Draw the graph of this linear equation. Check if the point (5, 15) lies on the graph.
Solution not provided.
Ans. y = 3x; Yes
Draw the graph of the equations 3x + 4y = 7 and 3x – 2y = 1 and find the point of intersection of lines representing the equations.
Solution not provided.
Ans. (1, 1)
Find the value of k if x = 2, y = 1 is a solution of the equations 2x +3y = k and 3x + y = k.
Solution not provided.
Ans. k = 7
Give the equations of two lines passing through (–3, 4). How many more such lines are possible?
Solution not provided.
Ans. x + y + 1 = 0, 2y + x = 2, 3y + x =9; infintely many
The cost of a pen is र 6 more than two times the cost of a pencil. Write a linear equation in two variables to represent this statement and draw the graph of the linear equation obtained.
Solution not provided.
Ans. y = 2x + 6
The cost of a toy telephone is the same as cost . of 4 balls. Express this statement as a linear equation in two variables. Also, find the cost of getting 2 toy telephone packed, if cost of 1 ball is र 5 and there is a fixed cost of र 2 for packing a toy telephone.
Solution not provided.
Ans. y =4x; Rs. 44
Determine the co-ordinates of a point on the graph of 5x – y = 12 whose
(a) ordinate is twice that of the abscissa
(b) abscissa and ordinate are in the ratio 3 : 2.
Solution not provided.
Ans. (4, 2) (b) ![]()
A rectangular field has to be cut out and its boundary marked with fencing with a given wire of length 100 m.
(a) Represent the above situation using a linear equation
(b) Also plot its graph
Solution not provided.
Ans. (a) d + y = 50
Which of the following statements are true and which are false? Give reasons for your answers:

(i) Only one line can pass through a single point.
(ii) There are an infinite number of lines which pass through two distinct points.
(iii) A terminated line can be produced indefinitely on both the sides.
(iv) If two circles are equal, then their radii are equal.
(v) In figure, if AB = PQ and PQ = XY, then AB = XY.
(i) False. This can be seen usually.
(ii) False. This contradicts Axiom 5.1.
(iii) True. Postulate 2.
(iv) True. If we superimpose the region bounded by one circle on the other, then they coincide. So, their centres and boundaries coincide therefore, their radii will coincide.
(v) True. The first Axiom of Euclid.
Give a definition for each of the following terms. Are there other terms that need to be defined first ? What are they, and how might you define them?
(i) parallel lines (ii) perpendicular lines
(iii) line segment (iv) radius of a circle
(v) square.
(i) Parallel lines. Lines which do not intersect anywhere are called parallel lines.
(ii) Perpendicular lines. Two lines which are at a right angle to each other are called perpendicular lines.
(iii) Line segment. It is a terminated line.
(iv) Radius. The length of the line-segment joining the centre of a circle to any point on its circumference is called its radius.
(v) Square. A quadrilateral with all the four sides equal and all the four angles of measure 90° each is called a square.
Consider two ‘postulates’ given below:
(i) Given any two distinct points A and B, there exists a third point C which is in between A and B.
(ii) There exist at least three points that are not on the same line.\
Do these postulates contain any undefined terms ? Are these postulates consistent? Do they follow from Euclid’s postulates ? Explain.
Yes! These postulates contain two undefined terms: Point and Line.
Yes! These postulates are consistent because they deal with two different situations (i) say that given two points A and B, there is a point C lying on the line in between them, (ii) say that given A and B, we can take C not lying on the line through A and B. These ‘postulates’ do not follow from Euclid’s postulates however, they follow from Axiom 5.1.
If a point C lies between two points A and B such that AC = BC, then prove that AC =  AB. Explain by drawing the figure.
AB. Explain by drawing the figure.
AC = BC
AC + AC = BC + AC
| Equals are added to equals
| BC + AC coincided with AB
| Things which are equal to the same point are equal to one another.
In Question 4, point C is called a mid-point of line segment AB. Prove that every line segment has one and only one mid-point.
In figure, if AC = BD, then prove that AB = CD.

AC = BD | Given ...(1)
AC = AB + BC
| Point B lies between A and C ...(2)
BD = BC + CD
| Point C lies between B and D ...(3)
Substituting (2) and (3) in (1), we get
AB + BC = BC + CD ⇒ AB = CD.
| Subtracting equals from equals
Why is Axiom 5, in the list of Euclid’s axioms, considered a ‘universal truth’? (Note that the question is not about the fifth postulate).
In figure, AC = XD, C is the mid point of AB and D is the mid point of XY. Using an Euclid’s axiom, show that AB = XY.
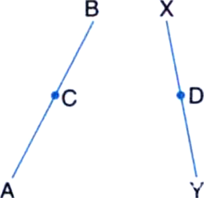
AC = XD | Given
⇒ 2AC = 2XD
| Things which are double of the same things are equal to one another
⇒ AB = XY
| ∵ C is the mid-point of AB and D is the mid-point of XY
In the given figure, it is given that ∠1 = ∠4 and ∠3 = ∠2. By which Euclid's axiom, it can be shown that if ∠2 = ∠4, then ∠1 = ∠3.
∠2 = ∠4 ...(1) | Given
∠1 = ∠4 ...(2) | Given
∠3 = ∠2 ...(3) | Given
From (1),
∠4 = ∠2 ...(4)
From (3) and (4),
∠3 = ∠4 ...(5)
| Things which are equal to the same thing are equal to one another
From (2) and (4),
∠1 = ∠3
|Things which are equal to the same thing are equal to one another
If A, B and C are three points on a line, and B lies between A and C, then prove that AB + BC = AC.

Solution not provided.
Prove that an equilateral triangle can be constructed on any given line segment.
Solution not provided.
Prove that two distinct lines cannot have more than one point in common.
Solution not provided.
How would you rewrite Euclid’s fifth postulate so that it would be easier to understand?
Does Euclid’s fifth postulate imply the existence of parallel lines? Explain.
If a straight line l falls on two straight lines m and n such that sum of the interior angles on one side of l is two right angles, then by Euclid’s fifth postulate the lines m and n will not meet on this side of I. Next, we know that the sum of the interior angles on the other side of line l will also be two right angles.
Therefore, they will not meet on the other side also. So, the lines m and n never meet and are, therefore parallel.
Which of the following statements is incorrect?
-
A line segment has definite length
-
Three lines are concurrent if and only if they have a common point
-
Two lines drawn in a plane always intersect at a point
-
One and only one line can be drawn passing through a given point and parallel to a given line
C.
Two lines drawn in a plane always intersect at a point
Which one of the following statements is true?
-
Only one line can pass through a single point.
-
There are an infinite number lines which pass through two distinct points.
-
Two distinct lines cannot have more than one point in common.
-
If two circles are equal, then their radii are not equal.
C.
Two distinct lines cannot have more than one point in common.
Select the wrong statement:
-
Only one line can pass through a single point.
-
Only one line can pass through two distinct points.
-
A terminated line can be produced indefinitely on both the sides.
-
If two circles are equal, then their radii are equal.
A.
Only one line can pass through a single point.
The number of lines that can pass through a given point is:
-
Two
-
None
-
Only one
-
Infinitely many
D.
Infinitely many
Two planes intersect each other to form a:
-
plane
-
point
-
straight line
-
angle
C.
straight line
The things which coincide with one another are:
-
equal to another
-
unequal
-
double of same thing
-
triple of same thing
A.
equal to anotherMock Test Series
Sponsor Area
Sponsor Area