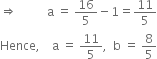5. If x = –2, y = 6 is solution of equation 3ax + 2by = 6, then find the value of b from 2(a – 1) + 2(3b – 4) = 4.

Solution

If x = –2, y = 6 is solution of equation
3ax + 2by = 6, then
3a(-2) + 2b(6) = 6
$rightwards double arrow$ -6a + 12b = 6
$rightwards double arrow$ -a + 2b = 1 ...(1)
| dividing throughout by 6
Also
2(a - 1) + 2(3b - 4) = 4
$rightwards double arrow$ 2a - 2 + 6b -8 = 4
$rightwards double arrow$ 2a + 6b = 14
$rightwards double arrow$ a + 3b = 7 ....(2)
| Dividing throughout by 2
Adding (1) and (2), we get
5b = 8 $rightwards double arrow$ b = $8 over 5$
Putting b = $8 over 5$ in (1), we get
$negative straight a plus 2 open parentheses 8 over 5 close parentheses equals 1$
$rightwards double arrow space space space space space space space space space space straight a space equals space 16 over 5 minus 1 equals 11 over 5 Hence comma space space space space straight a space equals space 11 over 5 comma space space straight b space equals space 8 over 5$