Mathematics Chapter 14 Statistics
Sponsor Area
NCERT Solution For Class 10 Mathematics
2 cubes each of volume 64 cm3 are joined end to end. Find the surface area of the resulting cuboid.
Let ‘a’ be the length of a side of a cube. Then
Volume of one cube = 64 cm3
⇒ n3 = 65 cm3
⇒ n = 4 cm
On joining the cubes, a cuboid is formed.
Then The length of the resulting cuboid (l) = 2
The breadth of the resulting cuboid (b) = a cm
The thickness of the resulting cuboid (h) = a cm
Now,
Surface area of the resulting cuboid
= 2(lb + bh + hl)
= 2 (2a. a + a. a + a. 2a)
= 2 (2a2 + a2 + 2a2)
= 2 (5a2) = 10a2 = 10 (4)2
= 160 cm2.
A vessel is in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is 14 cm and the total height of the vessel is 13 cm. Find the inner curved surface area of the vessel.
Let r cm be the radius of the cylinder and h cm be the height of the cylinder, then
r = 7 cm,
and h = (13–7) cm
= 6 cm.
Let r1 cm be the radius of the hemisphere, then
r1 = 7 cm
Now,
the inner curved surface area of the vessel
= C,S.A of hemisphere
+ C,S.A of cylinder
= (2πr12 + 2 π rh) cm2
= (2 π r2 + 2 π rh) cm2 [∵ r1 = r]
= [2 π r (r + h)] cm2
![]()
= (44 x 13) cm2
= 572 cm2.
A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. The total height of the toy is 15.5 cm. Find the total surface area of the toy.
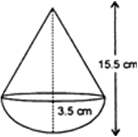
r = 3.5 cm,
h = (15.5 – 3.5) cm = 12 cm.
Now, l = 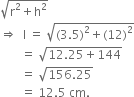
Then, r1 = 3.5 cm [∵ r = r1]
Now,
The total surface area of the toy
= CSA of hemisphere
+ CSA of cone
= 2 π r12 + πrl
= 2π r2 + πrl [ ∵ r1= r]
= π r [2r + l]
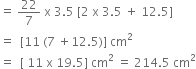
A cubical block of side 7 cm is surmounted by a hemisphere. What is the greatest diameter the hemisphere can have? Find the surface area of the solid.
Let a be the length of an edge of the cube. Then
a = 7 cm
Greatest diameter of the hemisphere
= Length of an edge of the cube
= 7 cm
Now,
Surface area of the cube
= 6 (edge)2
= 6 x 72
= 6 x 49 = 294 cm2
Let r be the radius of the hemisphere.
Then, r = ![]()
Now,
Curbed surface area of hemisphere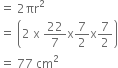
And, Base area = ![]()
![]()
Total surface area
= Surface area of the cube + curved surface area of the hemisphere – base area of the hemisphere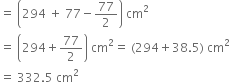
A hemispherical depression is cut out from one face of a cubical wooden block such that the diameter l of the hemisphere is equal to the edge of the cube. Determine the surface area of the remaining solid.
It is given that,
Edge of the cube = l
Then, Surface area = 6 (edge)2 = 6l2
Now, the greatest diameter of hemisphere
= length of an edge of the cube
= l
So, curved surface area of the hemisphere
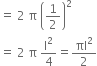
And, Area of base of the hemisphere

Required surface area
= Surface area of the cubical wooden block – area of the base of the hemisphere + curved surface area of the hemisphere![]()
A medicine capsule is in the shape of a cylinder with two hemispheres stuck to each of its ends (see Fig. 13.10). The length of the entire capsule is 14 mm and the diameter of the capsule is 5 mm. Find its surface area.

Let r mm be the radius and h mm be the height of the cylinder, then
r1 = 2.5 mm
and h = (14 – 5) mm = 9 mm
Now,
Surface Area of Capsule
= CSA of cylinder + CSA of two
hemispherical ends = 2πr1h + 2(2πr2)
= (2πr1h + 4πr2) mm2
= (2πrh + 4πr2) mm2 [∵ r1 = r]
= [2πr (h + 2r)]mm2
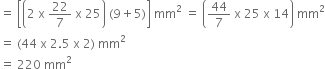
A tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are 2.1 m and 4 m respectively, and the slant height of the top is 2.8 m, find the area of the canvas used for making the tent. Also, find the cost of the canvas of the tent at the rate of Rs 500 per m2. (Note that the base of the tent will not be covered with canvas.)
Let r m be the radius and l m be the slant height of the cone, then
r = 2 m, and l = 2.8 m
Let r1 m be the radius and h m be the height of the cylinder, then
Now, r1 – 2 m and h = 2.1 m
Area of the canvas used
= CSA of cone + CSA of cylinder
= πrl + 2 πr1h
= πrl + 2πrh [r = r1]
= π r (l + 2h) m2 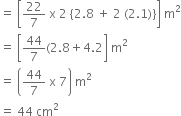
and Cost of canvas of the tent
= Rs. (500 x 44)
= Rs. 22,000.
From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest cm2.
Let r cm be the radius and h cm be the height of the cylinder, then
r = 0.7 cm and h = 2.4 cm.
Let r1 cm be the radius, l cm be the slant height and h1 cm be the height of the cone, then
r1 = 0.7 cm and h1 = 2.4 cm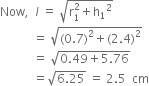
Now,
Total surface area of the remaining solid
= (C.S.A of cylinder) + (C.S.A of cone) + (area of upper base of the cylinder)
= 2 π rh + πr2l + πr2
= 2 π rh + π rl + π r2 [ ∵ r = r1]
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in Fig. 13.11. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.
Let r cm be the radius and h cm be the height of cylinder, then
r = 3.5 cm
and
h = 10 cm.
Let r1 be the radius of the hemisphere, then r1 = 3.5 cm.
Now,
Total Surface area of the article
= Curved Surface Area of the cylinder + 2 (Curved Surface area of hemisphere)
= 2 π rh + 2(2 π r12)
= 2 π rh + 4 π r 2
= 2 π rh + 4 π r2 [∵ r = r1]
= [2 π r (h + 2r)] cm2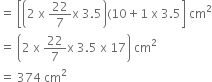
A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of π.
Let r cm be the radius of the hemisphere, then r = 1 cm.
Let R be the radius of the cone and h cm be the height. Then
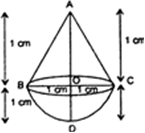
R = 1 cm and h = 1 cm
[It is given that R = h)
Now, Volume of solid
= Volume of hemisphere + volume of cone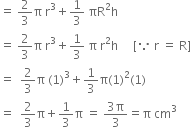
Rachel, an engineering student, was asked to make a model shaped like a cylinder with two cones attached at its two ends by using a thin aluminium sheet. The diameter of the model is 3 cm and its length is 12 cm. If each cone has a height of 2 cm, find the volume of air contained in the model that Rachel made. (Assume the outer and inner dimensions of the model to be nearly the same.)
Let r cm be the radius and h cm be the height of a cone, then
r = 1.5 cm, and h = 2 cm,
Now, Volume of conical part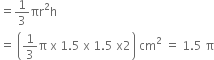
Let r cm be the radius and h cm be the height of the cylindrical part then r1 = 1.5 cm, h1= 8 cm
Now, Volume of cylindrical part
= πr12 h’
= (π x 1.5 x 1.5 x 8) cm3 = 18 π cm3
Hence, the volume of air contained in the model that Rachel made
= Volume of two conical part + Volume of cylindrical part
= (2 x 1.5 π + 18 π) cm3
= (3 π + 18 π) cm3
= (21 π) cm3![]()
A gulab jamun, contains sugar syrup up to about 30% of its volume. Find approximately how much syrup would be found in 45 gulab jamuns, each shaped like a cylinder with two hemispherical ends with length 5 cm and diameter 2.8 cm (see Fig. 13.15).
Fig. 13.17.

Now,
Volume of hemispherical part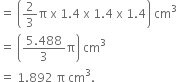
Let R cm be the radius and H cm be the height of cylinndrical part, then![]()
and H = 5 cm – (2 x 1.4) cm = 2.2 cm
Now,
Volume of cylindrical part
= πR2H = (πx1.4 x 1.4 x 2.2)cm3
= 4.312 π cm3.
Now,
Volume of each Gulab Jamun
= Volume of cylindrical + 2 (Volume of hemispherical part)
= (4.312 π + 2(1.829) π] cm3
= (4.312 π + 3.658 π) cm = 7.97 π![]()
Hence,
Volume of syrup found in 45 Gulab Jamuns
= 45 x 30% of volume of each Gulab Jamun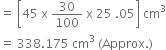
A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboid are 15 cm by 10 cm by 3.5 cm. The radius of each of the depressions is 0.5 cm and the depth is 1.4 cm. Find the volume of wood in the entire stand (see the given Fig.).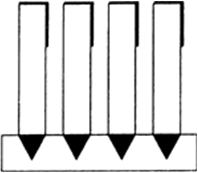
Let l, b and h be respectively the length, breadth and height of a cuboid, then
l = 15 cm
b = 10 cm
and h = 3.5 cm
Volume of cuboid
= (l x b x h) cm3 = (15 x 10 x 3.5) cm3
= 525 cm3
Let r cm be the radius and h cm be the height of conical part, the
r = 0.5 cm, h = 1.4 cm
Now,
Volume = 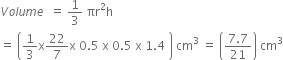
Hence, the volume of wood in the entire stand
= Volume of cuboid - 4 (Volume of cone)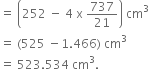
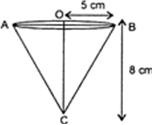
A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open, is 5 cm. It is filled with water up to the brim. When lead shots, each of which is a sphere of radius 0.5 cm are dropped into the vessel, one-fourth of the water flows out. Find the number of lead shots dropped in the vessel.
Let r cm be the radius and h cm be the height of the cone. Then r = 5 cm and h = 8 cm.

A solid iron pole consists of a cylinder of height 220 cm and base diameter 24 cm, which is surmounted by another cylinder of height 60 cm and radius 8 cm. Find the mass of the pole, given that 1 cm3 of iron has approximately 8g mass. (Use π = 3.14)
Let h cm be the height and r cm be the radius of the first cylinder. Then
h = 220 cm and r = ![]() = 12 cm
= 12 cm
Now, Volume = πr2 h
= (π x 12 x 12 x 220) cm3
= 31680 π
Let H cm be the height and R cm be the radius of the second cylinder. ThenH = 60 cm and R = 8 cm
Now, Volume = ![]()
![]()
Total volume of the pole
= 31680 ![]() + 3840
+ 3840 ![]()
= 35520 ![]() = (35520 x 3.14) cm3
= (35520 x 3.14) cm3
= 111532.8 cm3
Now, Required weight
= ![]()
A solid consisting of a right circular cone of height 120 cm and radius 60 cm standing on a hemisphere of radius 60 cm is placed upright in a right circular cylinder full of water such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is 60 cm and its height is 180 cm.
r = 60 cm, h = 120 cm
Volume of cone =
=
Let r1 cm be the radius of a hemisphere then
r1 = 60 cm
Now,
Volume of hemisphere =
Let R cm be the radius and H cm be the height of a cyclinder, then
R = 60 cm, H = 180 cm
Now,
Volume of Cylinder = πR2H
= (π x 60 x 60 x 180) cm3
= (π x 64800) cm3
= 648000 π cm3.
Volume of Solid
= Volume of cone + volume of hemisphere
= (144000π + 144000π) cm3
= 288000π cm3 Hence,
Volume of water left in the cylinder
= Volume of cylinder – Volume of solid
= 1648000 π – 288000 π) cm3
= 360000 π cm3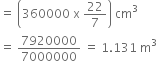
A spherical glass vessel has a cylindrical neck 8 cm long, 2 cm in diameter; the diameter of the spherical part is 8.5 cm. By measuring the amount of water it holds, a child finds its volume to be 345 cm3. Check whether she is correct, taking the above as the inside measurements and π = 3.14.
Let r cm be the radius of the spherical glass. Then
![]()
Now,
Volume = ![]()
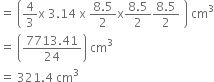
Let R cm be the radius and h cm be the height of cylindrical part.
Then, R = ![]() = 1 cm, h = 8 cm
= 1 cm, h = 8 cm
Volume = ![]()
= (3.14 x 1 x 1 x 8) cm3
= (25.12) cm3
Quantity of water = (321.4 + 25.12) cm3
= 346.52 cm3
Hence, Answer is not correct.
Sponsor Area
A metallic sphere of radius 4.2 cm is melted and recast into the shape of a cylinder of radius 6 cm. Find the height of the cylinder.
Let r cm be the radius of the sphere. Then, r = 4.2 cm
Now,
Volume = ![]()
![]()
Let R cm be the radius and h cm be the height at the cylinder. Then
R = 6 cm and h = ?
Now, Volume = πR2h
= (π x 6 x 6 x h) cm3
∵ Since sphere is recast into the shape of a cylinder. So, volume remains same![]()
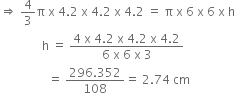
Metallic spheres of radii 6 cm, 8 cm and 10 cm, respectively, are melted to form a single solid sphere. Find the radius of the resulting sphere.
Let r1 r2, and r3 be the radius of metallic spheres, then r1 = 6 cm, r2 = 8 cm, r3 = 10 cm.
Let R cm be the radius of a single solid sphere.
Since, three metallic spheres are formed from a single solid sphere, so their volumes are equal.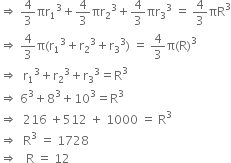
Hence, radius of sphere = 12 cm
A 20 m deep well with diameter 7 m is dug and the earth from digging is evenly spread out to form a platform 22 m by 14 m. Find the height of the platform.
Then, r =
Now,
Volume of earth dug out =
= 770 m3
Area of embankment
= 22 m x 14 m
= 308 m2

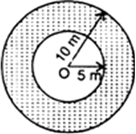
A well of diameter 3 m is dug 14 m deep. The earth taken out of it has been spread evenly all around it in the shape of a circular ring of width 4 m to form an embankment. Find the height of the embankment.

A container shaped like a right circular cylinder having diameter 12 cm and height 15 cm is full of ice cream. The ice cream is to be filled into cones of height 12 cm and diameter 6 cm, having a hemispherical shape on the top. Find the number of such cones which can be filled with ice cream.
Let R cm be the radius and H cm be the height of a container, then
Therefore, volume of cylindrical container
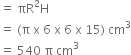
Let r1 cm be the radius and h cm be the height of a cone, then
Therefore, Volume of conical part
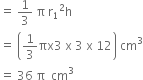
Let r2 cm be the radius of hemispherical part then
Therefore, Volume of Hemispherical part
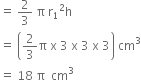
Now, Volume of ice-creme cone with hemispherical top
= Volume of cone + Volume of Hemisphere
= (36
= 54
Therefore,
the required no. of such cones

How many silver coins, 1.75 cm in diameter and of thickness 2 mm, must be melted to form a cuboid of dimensions 5.5 cm × 10 cm × 3.5 cm?
Now, Volume =
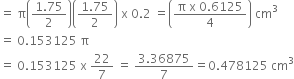
Let l, b and h are respectively the length, breadth and height of the cuboid. Then
l = 5.5 cm, b = 10 cm and h = 3.5 cm
Now, Volume = l x b x h
= (5.5 x 10 x 3.5) cm3 = 192.5 cm3
Hence, Required number of silver coins
A cylindrical bucket, 32 cm high and with radius of base 18 cm, is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm, find the radius and slant height of the heap.
Let r cm be the radius and l cm be the slant height of the bucket (cylindrical). Then
r = 18 cm and h = 32
Now, Volume = πr2h
= π (18)2 (32)
= (π x 18 x 18 x 32) cm3
Let r cm be the radius and h cm be the height of the conical heap. Then
r = ? and h = 24 cm
Now, Volume = ![]()
![]()
Since sand of bucket is emptied on the ground and a conical heap of sand is formed. So, volume remains same
i.e. ![]() x 18 x 18 x 32 =
x 18 x 18 x 32 = ![]()
Water in a canal, 6 m wide and 1.5 m deep, is flowing with a speed of 10 km/h. How much area will it irrigate in 30 minutes, if 8 cm of standing water is needed?
We have,
Width of the canal = 6 m
Depth of the canal = 1.5 m
It is given that the water is flowing with velocity 10 km/hr. Therefore, length of the water column formed in ![]() hr (30 minutes) = 5 km = 5000 m.
hr (30 minutes) = 5 km = 5000 m.
∴ Volume of the water flowing in 30 minutes = volume of cuboid at of length 5000 m, width 6 m and depth 1.5 m.
⇒ Volume of the water flowing in 30 minutes
= (5000 x 6 x 1.5) m3
= 45000 m3
Suppose x m2 area is irrigated in ![]() hr.
hr.
Then, x x ![]() = 45000
= 45000![]()
Hence, the canal irrigates 562500 m2 area in ![]() hour.
hour.
A farmer connects a pipe of internal diameter 20 cm from a canal into a cylindrical tank in her field, which is 10 m in diameter and 2 m deep. If water flows through the pipe at the rate of 3 km/h, in how much time will the tank be filled?
Then, r =
Now, volume of cylindrical tank
Now, Volume of the water that flows through the pipe t hours
= Volume of cylinder of radius of 10 cm and length (3000f m)
= 1 hour 40 minutes
A drinking glass is in the shape of a frustum of a cone of height 14 cm. The diameters of its two circular ends are 4 cm and 2 cm. Find the capacity of the glass.
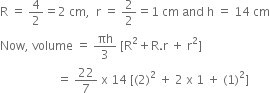
= 44 (4 + 2 + 1)
= 44 x 7 = 308 cm3
The slant height of a frustum of a cone is 4 cm and the perimeters (circumference) of its circular ends are 18 cm and 6 cm. Find the curved surface area of the frustum.
Let R and r be the radii of bigger and smaller ends of the frustum, and l be the slant height, then l = 4cm.
Perimeter of bigger end = 18 cm
⇒ 2 πR = 18
⇒ π R = 9 cm
Perimeter of smaller end = 6 cm
⇒ 2 πr = 6
⇒ πr = 3 cm
Now,
Curved Surface of the fustum
= πRl + πrl
= 1 (πR + πr)
= 4 (9 + 3)
= 4 x 12
= 48 cm2.
A fez, the cap used by the Turks, is shaped like the frustum of a cone (see Fig. 13.24). If its radius on the open side is 10 cm, radius at the upper base is 4 cm and its slant height is 15 cm, find the area of material used for making it. 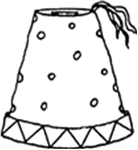
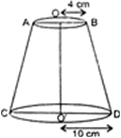
R = 10 cm; r = 4 cm and l = 15
Now,
Curved Surface Area
= π Rl + πrl
= πl (R + r)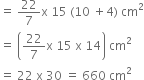
and area of the top of the cap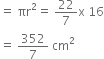
Thus,
Total area of the material used for making the cap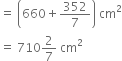
A container, opened from the top and made up of a metal sheet, is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm, respectively. Find the cost of the milk which can completely fill the container, at the rate of ` 20 per litre. Also find the cost of metal sheet used to make the container, if it costs ` 8 per 100 cm2 . (Take π = 3.14)
Let R and r be respectively the radii of bigger and smaller ends of the frustum, then
R = 20 cm, r = 8 cm
Let l and h be respectively the slant height and height of the frustum then
h = 16 cm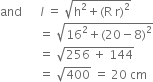
Now,
(i) Curved Surface area of frustum
= πl (R + r)
= 3.14 x 20 (20 + 8)
= (3.14 x 20 x 28) cm2
= 1758.4 cm2
(ii) Total tin required
= CSA. + area of base
= 1758.4 + 3.14 x (8)2
= 1758.4 + 200.96
= 1959.36 cm2
(iii) Cost of required tin![]()
(iv) Volume of frustum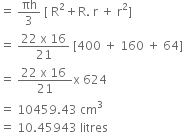
Now,
Cost of the milk which can completely fill the container at the rate of 20 per litre
= 10.46 x 20
= Rs. 209.20
Hence, cost of milk is Rs. 209 and cost of metal is Rs. 156.75.
A metallic right circular cone 20 cm high and whose vertical angle is 60° is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained be drawn into a wire of diameter ![]() , find the length of the wire.
, find the length of the wire.
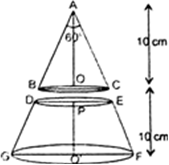
It is given that ∠BAC = 60° ∠OAC = 30°
In right triangle AOC, tan
And, C =

Height of the frustum = P'O =
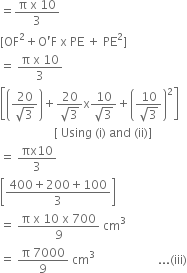
Radius of the wire =
Let h be length of the wire
From (iii) and (iv), we get
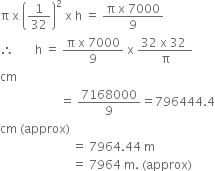
A copper wire, 3 mm in diameter, is wound about a cylinder whose length is 12 cm, and diameter 10 cm, so as to cover the curved surface of the cylinder. Find the length and mass of the wire, assuming the density of copper to be 8.88 g per cm3.
Length of the cylinder = 12 cm = 120 mm
∵ Number of rounds to cover 3 mm = 1
∴ Number of rounds to cover 120 mm
![]()
Let r cm be the radius of the cylinder, Then
![]()
![]() Length of the wire in completing one round
Length of the wire in completing one round
= 2![]()
= 2![]() (5) = 10
(5) = 10 ![]() cm
cm![]() Length of the wire in completing the whole surface (40 rounds)
Length of the wire in completing the whole surface (40 rounds)
= 10 ![]() x 40 = 400
x 40 = 400 ![]() cm
cm
Radius of the copper wire = ![]()
![]() Volume of wire =
Volume of wire = ![]()
= ![]()
![]() Mass of wire =
Mass of wire = ![]()
= 79.92 ![]()
A right triangle, whose sides are 3 cm and 4 cm (other than hypotenuse) is made to revolve about its hypotenuse. Find the volume and surface area of the double cone so formed. (Choose value of π as found appropriate.)
In right triangle CAB :
BC2 = AB2 + AC2
[Using Pythagoras theorem]
⇒ BC2 = 32 + 42
⇒ BC2 = 9 + 16 = 25
⇒ BC = 5 cm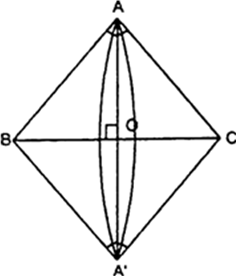
Now, in ΔAOB and ΔCAB :
∠AOB = ∠CAB (90°)
∠B = ∠B
[Common]
Therefore, by using A A similar condition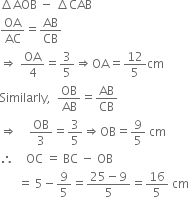
Now,
Volume of the double cone so formed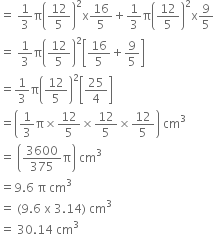
and Surface area of the double cone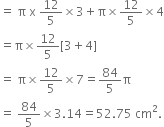
A cistern, internally measuring 150 cm × 120 cm × 110 cm, has 129600 cm3 of water in it. Porous bricks are placed in the water until the cistern is full to the brim. Each brick absorbs one-seventeenth of its own volume of water. How many bricks can be put in without overflowing the water, each brick being 22.5 cm × 7.5 cm × 6.5 cm?
Volume of water in the cistern
= 129600 cm3
Let l, b and h are the length, breadth and height of the cistern. Then
l = 150 cm, b = 120 cm and h = 110 cm
Now, Volume of cistern = l x b x h
= 150 x 120 x 110 = 1980000 cm3
∴ Volume of cistern to be filled
= (1980000 – 129600) cm3
= 1850400 cm3
Volume of one brick
= (22.5 x 7.5 x 6.5) cm3
= 1096.875 cm3
Let the total number of bricks be x.
then, water absored by x bricks
![]()
![]() Volume of the water left in the cistem
Volume of the water left in the cistem
![]()
Since, the cistern is filled upto the brim. Therefore,
Volume of the cistern
= Volume of the water left in the cistern + volume of the bricks![]()
Hence, total no of bricks = 1792 (approx).
In one fortnight of a given month, there was a rainfall of 10 cm in a river valley. If the area of the valley is 7280 km2, show that the total rainfall was approximately equivalent to the addition to the normal water of three rivers each 1072 km long, 75 m wide and 3 m deep.
Volume of three rivers
Hence, the two are approxmately equivalent.
An oil funnel made of tin sheet consists of a 10 cm long cylindrical portion attached to a frustum of a cone. If the total height is 22 cm, diameter of the cylindrical portion is 8 cm and the diameter of the top of the funnel is 18 cm, find the area of the tin sheet required to make the funnel (see the given Fig.
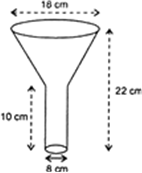
Let l and h be respectively the slant height and height of frustum, then
h = total height – height of cylindrical part
= 22 cm – 10 cm
= 12 cm
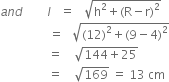
Now,
Curved surface area of frustum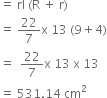
Let r1 and h1 be respectively the radius and height of cylindrical part.
Then, r1 = 4cm and h1 = 10cm
Now,
Curved Surface area of the cylinder
= 2πr1h 1![]()
Hence,
Area of tin required
= Curved surface area of frustum + curved surface area of cylinder
= 531.14 + 251.43
= 782.57 cm2.
Derive the formula for the curved surface area and total surface area of the frustum of a cone, given to you in Section 13.5, using the symbols as explained.
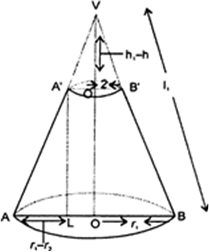
Let h be the height, l the slant height and r1 and r2 the radii of the circular bases of the frustum ABB’ A’ shown in Fig. such that r1 > r2.
Let the height of the cone VAB be h1 and its slant height be i.e., VO = h1 and VA = VB = l1
∴ VA’ = VA – AA’ = l1– l
and VO’ = VO – OO’ = h1– h
Here, ΔVOA ~ ΔVO‘A’
Now,
Height of the cone VA‘B’![]()
Slant height of the cone VA‘B’![]()
Let S denote the curved surface area of the frustum of cone. Then,
S = Lateral (curved) surface area of cone VAB
- Curved surface area of cone VA‘B’
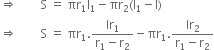
[Using (A) and (C)]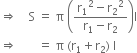
Curved surface area of the frustum
= π(r1 + r2)l
Total surface area of the frustum
= Lateral (curved) surface area
+ Surface area of circular bases
= π (r1 + r2) I + πr12 + πr22
= π {(r1 + r2) l + r12 + r22}.
Derive the formula for the volume of the frustum of a cone, given to you in Section 13.5, using the symbols as explained.
Let V be the volume of the frustum of cone. Then,
V = Volume of cone V AB
– Volume of cone VA ‘B’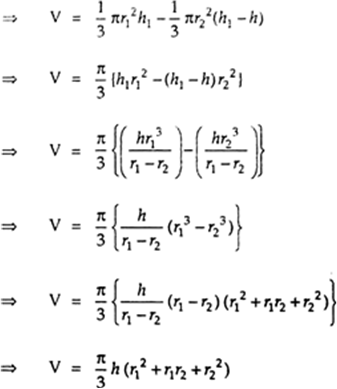
Thus, the volume of the frustum of the cone is given by![]()
The radius and height of a cylinder are in the ratio 5:7 and its volume is 550 cm3. Find its radius.
Now. Volume = 550
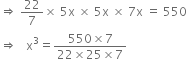
x = 1
∴ The required radius = 5x = 5 x 1 = 5cm.
Sponsor Area
The curved surface area of height circular cone is 12320 cm2. If the radius of the base is 56 cm, find its height.
Here, we have r = 56 cm
and, Curved Surface Area = 12320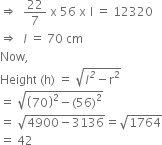
Hence, height of one cone = 42 cm.
A conical flask is full of mater. The flask was base m radius r and height n. the mater is poored into a cylindrical flask of base radius mr. find the height of water in the cylindrical flask.
Here, we have base radius of conical flask = r and height = h
Then,
Volume of conical flask = ![]()
Again,
Base radius of cylindrical flask = mr.
Let height of cylindrical flask = h
Then, volume = π (mr)2h1
Now,
Volume of Conical flask
= volume of cylindrical flask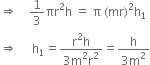
A cylinder, a cone and a hemisphere are of equal base and have the same height. What is the ratio of their volumes?
Let r be radius of a cylinder, a cone and a hemisphere respectively and h be the height of the cylinder, a cone and hemisphere respectively.
Then, h = r
V1 = Volume of a cylinder = ![]()
Now, V2 = Volume of a cone = ![]()
and V3 = Volume of a hemisphere = ![]()
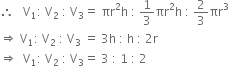
A cone and a hemisphere have equal bases and equal volumes. Find the ratio of their heights.
Let the radius of both cone and hemisphere be r cm.
Let h be the height of the cone.
It is given that,
Volume of a Cone = Volume of a hemisphere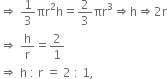
Hence, the ratio of the heights of a cone and hemisphere is 2 : 1.
If two cones have their volumes in the ratio 3 :1 and their heights are in the ratio 1 : 3, then find the ratio of their radius.
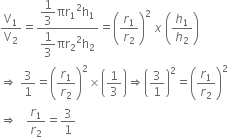
Thus, the ratio of their radius is 3 :1.
The radius of a solid hemispherical toy is 3.5 cm. Find the total surface area.
Here, we have
radius of hemispherical toy (r) = 3.5 cm
Now,
Total surface area = 3πr2![]()
If the number of square centimetres on the surface of a sphere is equal to the number of cubic centimetres in its volume, what is the diameter of the sphere?
It is given that
Volume of sphere = Surface Area of sphere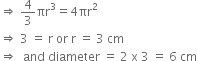
Determine the ratio of the volume of a cube to that of a sphere which will exactly fit inside the cube.
V1= (2r)3 and V2 =
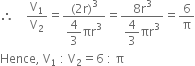
A cylinder and a cone are of the same base radius and of same height. Find the ratio of the volume of cylinder to that of the cone.
Let r be the base radius and h be the height.
Then, volume of the cylinder i. e.,
V1 = πr2h
and volume of the cone i.e.,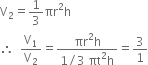
Hence, the required ratio is 3 : 1.
A right circular cylinder and a right circular cone have the same base radius and same height. What is the ratio of the volume of the cylinder to that of cone?
Let V and ‘R’ be the radii of cylinder and cone respectively.
And ‘h’ and ‘H’ be the heights of cylinder and cone respectively.
Now volume of cylinder (v1) = ![]()
And, volume of cone (v2) = ![]()
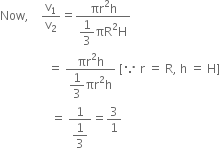
Find the depth of a cylindrical tank of radices 28 m, if its capacity is equal to that of a rectangular tank of size 28m x 16m x 11m..
Ans. 2m
A metallic sphere 1 dm in diameter is beaten into a circular sheet of uniform thickness equal to 1 mm. Find the radius of the sheet.
Ans. 4.08 cm.
Two cubes each of 10 cm edge are joined end to end. Find the surface area of the resulting cuboid.
Lei l, b and h are respectively the length, breadth and height of the cuboid, then
l = 10 cm + 10 cm 20 cm
b = 10 cm and h = 10 cm.
Now,
Surface Area of the cuboid
= 2 (lb + bh + hl)
= 2 (20 x 10+ 10 x 10+ 10 x 20) cm2
= 2 (200 + 100 + 200) cm2
= 1000 cm2.
Three cubes each of side 5 cm are joined end to end. Find the Surface Area of the resulting cuboid.
Let l, b and h are respectively the length, breadth and height of the cuboid, then
l = (5 + 5 + 5) cm = 15 cm
when three cubes are joined we get a cuboid
b = 5 cm and h = 5 cm.
Now,
The Surface Area of the resulting cuboid
= 2 (lb + bh + hl) cm2
= 2 (15 x 5 + 5 x 5 + 5 x 15) cm2
= 2 (75 + 25 + 75) cm2
= 2 (175) cm2
= 350 cm2.
Three equal cubes of side 4 cm are joined end to end. Find the surface area of the resulting cuboid.
Let l, b and h are respectively the length, breadth and height of the cuboid, then
l = (4 + 4 + 4) cm = 12 cm
when three cubes are joined we gel a cuboid.
So, b = 4 cm and h = 4 cm.
Now,
The Surface Area of the resulting cuboid
= 2 (lb + bh + hl) cm2
= 2 (12 x 4 + 4 x 4 + 4 x 12) cm2
= 2 (48 + 16 + 48) cm2
= (2 x 112) cm2
= 224 cm2.
Three cubes of metal whose edges are 6 cm, 8 cm and 10 cm are melted and a new cube is made (i) Find the length of the edge of the new cube.
(ii) Find the total surface area of the new cube.
Let the edges of the cubes of metal be a, b and c respectively, then
a = 6 cm, b = 8 cm and c = 10 cm
and thus respective volumes are,
v1 = (6)3, V2 = (8)3 and V3 = (10)3
Now, the volume of new cube
= V1 + V2 + V3
= 63 + 83 + 103
= 1748 = 123 cm3.
Let the length of the edge of the new cube be = a cm, then
a3 = 123 ⇒ a = 12 cm.
(ii) The total surface area of the new cube
= 6a2 = 6 x 12 x 12
= 864 cm2.
Two cubes each of 12 cm edge are joined end to end. Find the surface area of the resulting cuboid.
Let l, b and h are respectively the length, breadth and height of the cuboid, then
l = (12 + 12) cm = 24 cm
when two cubes are joined we get a cuboid b = 12 cm and h = 12 cm.
Now,
The Surface Area of the resulting cuboid
= 2 (lb + bh + hl) cm2
= 2 (24 x 12 + 12 x 12 + 24 x 12) cm2
= 2 (288 + 144 + 288) cm2
= 2 (720) cm2
= 1440 cm2.
Problems Based on Conversion of Solids from Shape to Another
A cone of height 24 cm and radius of base 6 cm is made up of modelling clay. A child reshapes it in the form of a sphere. Find the radius of the sphere.
Let the radius and height of a cone be 24 cm and 6 cm respectively, then
r = 6 cm, h = 24 cm
Let radius of the sphere be r1 cm,
Since, the volume of clay in the form of a cone and the sphere remains the same. Therefore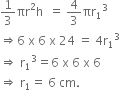
A right circular cone is 8 cm heigh and the radius of its base is 2 cm. The cone is melted and re-cast into a sphere. Determine the diameter of the sphere.
Let r cm be the radius and h cm be the height of the cone, then
r = 2 cm, h = 8 cm
Let r1 cm be the radius of the sphere.
Since, sphere is made out of the cone, so their volumes are equal.
Therefore,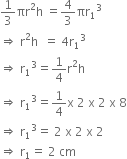
Hence, diameter of sphere = 4 cm.
A solid cylinder of metal 8 m high and 4 m diameter is melted and recast into a cone of diameter 3 m. Find the height of the cone.
h = 8 m
and r =
Let r1 m be the radius and m be the height of the cone, then
Since a cone is made out of the solid cylinder, so their volumes are equal.
Therefore,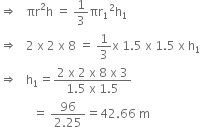
A cone is 8.4 cm high and the radius of its base is 2.1 cm. it is melted and recast into a sphere. Find the radius of the sphere.
Let r cm be the radius and h cm be the height of a cylinder, then
r = 2.1. cm, h = 8.4 cm
Let r1 cm be the radius of a sphere.
Since a sphere is made out of a cone, so their volumes are equal.
Therefore,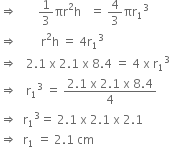
A well of diameter 14 m is dug 15 m deep. The earth taken out of it has been spread evenly all around it in the shape of a circular ring of width 7 m to form an embankment. Find the height of the embankment.
h = 15 m, r =
Now,
Volume of earth dug out =
[
= ( 22 x 7 x 15) m3
= 2310 m3
Let H m be the required height of the embankment.
Since the shape of the embankment will be like the shape of cylinder of internal radius (r2) 7 m and external radius (R1) = 7 + 7 = 14 m. Now,
the volume of embankment
= volume of the earth dug out
⇒ π(R12 –r12) H = 2310
⇒ π(142 – 72) H = 2310
⇒ π (196 – 49) H = 2310
⇒ π(147) H = 2310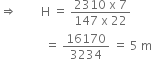
Hence, the height of the embakment = 5m
Alternative Method :
Height of the embankment![]()
Note :
Area of the embankment
= Area of ring
= π R2 – π r2
= π (R2 – π r2)
= π (R + r) (R – r)
An agriculture field is in the form of a rectangle of length 20 m, and width 14 m. A 10 m deep well of diameter 7 m is dug in a comer of the field and the earth taken out of the well is spread evenly over the remaining part of the field. Find the rise in the level of the field.
Since shape of the well is just like the shape of cylinder, so we consider well as cylinder.
Let r m be the radius and h m be the height of the well, then ![]()
Now,
Volume of earth dug out = ![]()
![]()
Also, we have,
Length of the rectangular field = 20 m
Breadth of the field = 14 m
Therefore, are of the field = (20 x 14) m2
= 280 m2
And
Area of the remaining part of the field
= Area of field - Area of the base
![]()
Since,
Volume of the raised field
= Volume of the earth dug out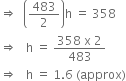
Hence, rise in the level of the field = 1.6 m (apporx.)
A metallic sphere of radius 10.5 cm is melted and recast into 5 small cones each of radius 3.5 cm and height 3 cm. Find how many cones are obtained.
Let R cm be the radius of the sphere, then
R = 10.5 cm
Now, Volume of sphere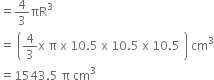
Let r cm be the radius and h cm be the height of the cone, then
r = 3.5 cm and h = 3 cm
Now, Volume of each cone
Therefore
Total number of cones
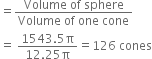
Find the number of coins 1.5 cm in diameter and 0.2 cm thick to be melted to form a right circular cylinder whose height is 8 cm and diameter 6 cm.
Since shape of the coin having thickness will be like a cylinder. So, we consider coin as a cylinder.
Let r cm be the radius and h cm be the height (thickness) of a coin, then![]()
Now, Volume of each coin
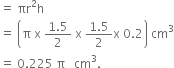
Let R cm be the radius and H cm be the height of a cylinder, then![]()
Now, Volume of cylinder
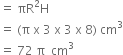
Therefore,
Total number of coins = ![]()
= ![]()
Spherical marbles of diameter 1.4 cm each are dropped in a cylindrical beaker of radius 3.5 cm containing some water. Find the number of marbles that should be dropped into the beaker so that the water level in the beaker rises by 5.6 cm.
Let ‘R’ cm be the radius of the sphere, then
R = 10.5 cm
Now, volume of sphere![]()
Let, ‘h’ cm be the rise in water level, and ‘r’ cm be the radius of the beaker. Then
r = 3.5 cm., h = 5.6 cm
Now, volume of cylinder = πr2h
= (π x 3.5 x 3.5 x 5.6) cm2
Therefore
Required no. of marbles
Hence, the required no. of marbles = 150
The radius of a conical solid is melted and recaste into a number of cylindrical solids if the radius of the cone is three times the radius of the cylinder and the height of the cone is four times the height of the cylinder, find the number of cylindrical solids.
Let R cm be the radius and H cm be the height of cone.
And r cm be the radius and h cm be the height of a cylinder, then
R = 3r
and H = 4h
Now,
Volume of cone = ![]()
and Volume of cylinder = π r2h Therefore,
The number of cylindrical solids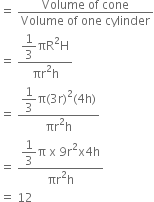
Water flows at the rate of 10 m per minute through a cylindrical pipe having its diameter as 5 mm. How much time will it take to fill a conical vessel whose diameter of the base is 40 cm and depth 24 cm.
[length of the water column in cylindrical pipe will become the height of cylindrical pipe]
Water is flowing at the rate of 0.70 m/sec through a circular pipe, whose internal diameter is 2 cm into a cylindrical tank the radius of whose base is 40 cm. Determine the increase in the water level in 1/2 hour.
[length of water column = Height of circular pipe]
Volume of water that flow's out of the circular pipe in 1 sec
= πR2H
= π x 0.01 x 0.01 x 0.70
= 0.00007 π m3.
Therefore, Volume of water that flows out of
the circular pipe in ![]() hr (30 x 60) sec
hr (30 x 60) sec
= (0.00007 ![]() x 1800) cm3
x 1800) cm3
= 0.126 ![]()
Let r m be the radius and h m be the height of cylindrical tank, then
r = 40 cm = ![]() = 0.4 m, h = ?
= 0.4 m, h = ?
Now, Volume of water in the cylindrical lank up to a height of h m
= πr2h = π x 0.4 x 0.4 x h = 0.1 6π h m2.
Since, Volume of the water flown into the tank
= Volume of the water that flows through the pipe in half an hour.
⇒ 0.16 π h = 0.126 π![]()
Hence, increase in water level in 1/2 hr = 7875 m.
Water in a canal 30 dm wide and 12 dm deep, is flowing velocity of 10 km/hr. How much area will it irrigate if 8 cm of standing water is required for irrigation?
We have,
Width of the canal = 30 dm = 300 cm = 3 m
Depth of the canal = 12 dm = 120 cm = 1.2 m
It is given that the water is flowing with velocity 10 km/hr. Therefore length of the water column formed in ![]() hour = 5 km = 5000 m
hour = 5 km = 5000 m
∵ Volume of the water flowing in ![]() hour
hour
= Volume of the cuboid of length = 5000 m,
Width = 3 m and depth = 1.2 m
= 5000 x 3 x 1.2 m3 = 18000 m3.
Suppose xm2 area is irrigated in ![]() hour. Then,
hour. Then,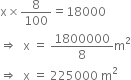
Hence, the canal irrigates 22500 m2 area in ![]() hour.
hour.
A hemispherical tank full of water is emptied by a pipe at the rate of litres per second. How much time will it take to half empty the tank, if the tank is 3 m in diameter.
Let r m be the radius of the hemispherical tank, then
![]()
Now, volume of hemispherical tank
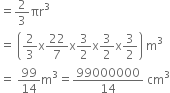
And, Volume of water to be emptied
![]() (Volume of hemispherical tabk)
(Volume of hemispherical tabk)
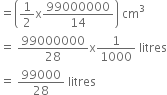
Hence,
Time taken to half empty the tank
![]()
= 16.5 minutes.
Sponsor Area
Water is flowing at the rate of 5 km per hour through a pipe of diameter 14 cm into a rectangular tank which is 50 m long and 44 m wide. Determine the time in which the level of water in the tank will rise by 7 cm.
r = 7 cm =
And, h = 5 km = 5000 m
[distance covered in 1 hr. = height of pipe]
Now, Volume of water that flows out of the circular pipe in 1 hour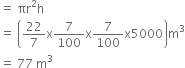
Let l, b and h are respectively the length, breath and height of the tank (cuboid), then
l = 50 m
b = 44 m
and h = 7 cm = ![]()
Now, Volume of water that flows in the rectangular tank
= l x b x h
![]()
![]() time taken to flow 77 m3 of water in to the tank K = 1 hr
time taken to flow 77 m3 of water in to the tank K = 1 hr![]() time taken to flow 154 m3 of water in to the tank =
time taken to flow 154 m3 of water in to the tank = ![]()
Hence, the level of water in the tank rise by 7 cm in 2 hrs.
Water is flowing at the rate of 3 km/ hr through a circular pipe of 20 cm external diameter into a circular cistern of diameter 10m and depth 2 m. In how much time will the cistern be filled.
H (depth) = 3 km = 3000 m.
Now, Volume of water that flows out of the circular pipe in 1 hour = πR2H![]()
Let r m be the radius and h m be the depth (height) of a circular cistern, then![]()
Now, Volume of water that flows in the circular cistern
= π r2h
= π x 5 x 5 x 2 = 50 π m3.
Hence,
Time taken to fill up the cistern
An iron solid sphere of radius 3 cm is melted and recast into small spherical balls of radius 1 cm each. Assuming that there is no wastage in the process, find the number of small spherical balls made from the given sphere.
So, Volume (V1) =
Let r be the radius of small spherical ball, then
r = 1 cm
So, Volume (V2) =
Now, Required number of small spherical balls
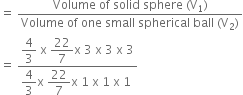
= 3 x 3 x 3 = 27
A spherical copper shell, of external diameter 18 cm, is melted and recast into a solid cone of base radius 14 cm and height  Find the inner diameter of the shell.
Find the inner diameter of the shell.
Let R be the external radius of the copper shell r be the internal radius, h be the height of the conical part and r1 be its radius.
Now, External d of copper shell = 18 cm.
A farmer connects a pipe of internal diameter 20 cm from a canal into a cylindrical tank in his field, which is 10 m in diameter and 2 m deep. If water flows through the pipe at the rate of 6km/h, in how much time will the tank be filled?
Speed of the water
= 6 k.m./hr. = 6000 m/hr.
i.e. length of the water column (h) = 6000 m
And, internal radius of the pipe (r)![]()
![]() Volume if water that flows in 1 hour =
Volume if water that flows in 1 hour = ![]()
![]()
Now, radius of the base of the tank (R)![]()
And, Depth of the tank (h = 2m)![]()
Hence, Required time to fill the tank by pipe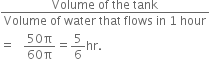
A cubical block of side 7 cm is surmounted by a hemisphere. What is the greatest diameter the hemisphere can have ? Find the surface area of the solid.
Solution not provided.
Ans. 7 cm, 332.5 cm2
Three cubes each of side 5 cm are joined end to end. Find the surface area of the resulting cuboid.
Solution not provided.
Ans. 350 cm2
Two cubes each of volume 64 m3 are joined end to end. Find the surface area and volume of the resulting cuboid.
Solution not provided.
Ans. 128 m2
Three cubes of side 6 cm are joined end to end. Find the surface area of the resulting cuboid.
Solution not provided.
Ans. 504 cm2
A piece of metal in the form of a cone of diameter 2 cm and height 9 cm is melted and recast into a cylinder of radius 1 cm. Find the height of the cylinder.
Solution not provided.
Ans. 3 cm
A cone 8.4 cm high and the radius of its base is 2.1 cm it is melted and recast into a sphere. Find the radius of the sphere.
Solution not provided.
Ans. 2.1cm
A copper rod of diameter 1 cm and length 8 cm is drawn into a wire of length 18 m of uniform thickness. Find the thickness of the wire.
Solution not provided.
Ans. 0.67mm (app.)
A metallic sphere of, radius 8 cm is melted into three spheres. Radii of two spheres are 6 cm and 4 cm. Find the radius of the third sphere.
Solution not provided.
Ans. ![]()
A right circular cone is 4.6 cm high and the radius of its base is 1.4 cm it is melted and recast into a right circular cone with radius 2.1 cm. Find its height.
Solution not provided.
Ans. 2.6 cm (app.)
The diameter of a metallic sphere is equal to 9 cm it is melted and drawn into a long wire of diameter 2 mm having uniform cross section. Find the length of the wire.
Solution not provided.
Ans. 12150 cm
A well, whose diameter is 7 m, has been dug 22.5 m deep and the earth dug out is used to form an embankment 10.5 m wide around it. Find the height of the embankment.
Solution not provided.
Ans. 1.5 m
A well of diameter 8 m is dug 14 m deep. The earth taken out of it is spread evently all around a width of 3m to form an embankment. Find the height of the embankment.
Solution not provided.
Ans. 6.78 m
An agricultural field is in the form of rectangle of length 22 m and width 14 m. A 20 m deep well of diameter 14 m is dug in a corner of the field and earth taken out of the well is spread evenly over the remaining part of the field. Find the rise in the level.
Solution not provided.
Ans. 10 m
How many silver coins 1.75 cm in diameter and of thickness 2 mm must be melted to form a cuboid dimensions 5.5. cm x 10 cm x 3.5 cm.
Solution not provided.
Ans. 400
How many spherical bullets can be made out of a solid cube of lead whose edge measures 44 cm each bullet being 4 cm in diameter.
Solution not provided.
Ans. 2541
How many balls each of radius 1 cm can be made from a solid sphere of lead of radius 8 cm.
Solution not provided.
Ans. 512
The diameter of a sphere is 42 cm. It is melted and drawn into a cylindrical wire of 28 cm diameter. Find the length of the wire.
Solution not provided.
Ans. 63 cm
How many spherical lead shots each 0.3 cm in diameter can be made from a rectangular solid (9 x 11 x 12) cm3.
Solution not provided.
Ans. 84000
A spherical shell of lead whose external diameter is 18 cm is melted and recast into a cylinder 8 cm high and 12 cm in diameter. Find the inner diameter of the shell.
Solution not provided.
Ans. 2(513)1/3 cm
A metallic sphere of radius 10.5 cm is melted and then recast into smaller cones, each of radius 3.5cm and height 3 cm. How many cones are obtained?
Solution not provided.
Ans. 63
Find the number of coins 1.5 cm in diameter and 0.2 cm thick to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm.
Solution not provided.
Ans. 450
Water in a canal 30 dm wide and 12 dm deep is flowing with a velocity of 20 km/hr. How much area will it irrigate in 30 minutes, if 9 cm of standing water is desired.
Solution not provided.
Ans. 400000 m2
Water flows in a tank 150 m x 100 m at the base through a pipe whose cross section is 2 dm by 1.5 dm at the speed of 15 km/hr. In what time will the water be 3 m deep.
Solution not provided.
Ans. 100 hrs.
Water is flowing at the rate of 3 km/hr through a circular pipe of 20 cm internal diameter into a circular cistern of diameter 10 m and depth 2 m. In how much time will the cistern be filled.
Solution not provided.
Ans. 1 hr 40 minutes.
Sponsor Area
A hemispherical tank of radius 1.75 m is full of water it is connected with a pipe which empties it at the rate of 7 litres per second. How much time will it take to empty the tank completely.
Solution not provided.
Ans. 26.73 minutes
Four right circular cylindrical vessels each having diameter 21 cm. and height 38 cm. are full of icecream. The icecream is to be filled in cones of height 12 cm and diameter 7cm having hemispherical shape at the top. Find the total number of such cones which can be filled with icecream.
Solution not provided.
Ans. 216
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder. If the height of the cylinder is 20 cm and radius of the base is 3.5 cm, find the total surface area of the article.
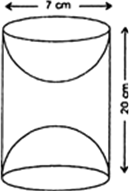
Let r cm be the radius, h cm be the height of the cylinder then
r = 3.5 cm
and h = 20 cm.
Let r1 be the radius of the hemisphere, then
r1 = 3.5 cm
Now,
Total surface area of the area of the article
= curved surface area of the cylinder
+ 2 (curved surface area of hemisphere)
= 2πrh + 2 (2 πr12)
= 2 πrh + 4 πr2 [∵ r = r1]
= 2 π r(h + 2r)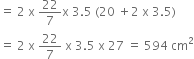
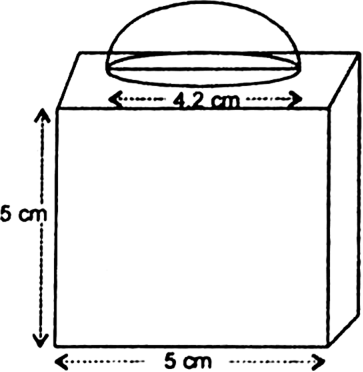
The decorative block shown in fig. is made of two solids - a cube and a hemisphere. The base of the block is a cube with edge 5 cm, and the hemisphere fixed on the top has a diameter of 4.2 cm. Find the total surface area of the block.
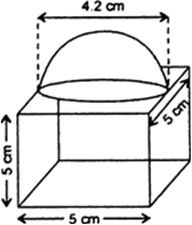
Let the side (edge) of the cube be a cm, then a
= 5 cm.
Let radius of the hemisphere be r, then
r = 2.1 cm
Now,
The total surface area of the block
= T.S.A of cube - base area of hemisphere + C.S.A of hemisphere
= 6 (side)2 – ![]() r2 + 2r
r2 + 2r![]() 2
2
= 150 – ![]() r2 + 2
r2 + 2 ![]() r2
r2
= 150 + ![]() 2
2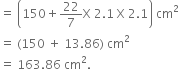
Tips: -
Mayank made a bird-bath for his garden in the shape of a cylinder with a hemispherical depression at one end. The height of the cylinder is 1.45 m and its radius is 30 cm. Find the total surface area of the birth - bath.

Let r cm be the radius and h cm be the height of the cylinder then,
r = 30 cm,
h = 1.45 m = 145 cm.
Lei r1 cm be the radius of the hemisphere, then
r1 = 30 cm
Now,
The Total Surface Area of the bird bath
= C.S.A of cylinder + C.S.A of Hemisphere
= 2 ![]() rh + 2
rh + 2 ![]() r1 2
r1 2
= 2![]() rh + 2
rh + 2![]() r2 [∵ r = r1]
r2 [∵ r = r1]
= [2 ∵ r (h + r)] cm2
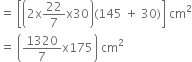
= 33000 cm2
= 3.3 m2
A rocket is in the form of a circular cylinder closed at the lower end and a cone of the same radius is attached to the top The radius of the cylinder is 2.5 m, its height is 21 m and the slant height of the cone is 8 m. Calculate the total surface area of the rocket.
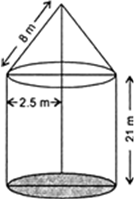
Let r m be the radius, and h m be the height of the cylinder, then
r = 2.5 m and h = 21 m
Let r m be the radius and l m be the slant height of the cone, then
r1 = 2.5 m and l = 8 m
Now,
The Total Surface Area of the rocket
= C.S.A of cone + C.S.A of cylinder + Area of base
= ![]() r1l + 2
r1l + 2 ![]() rh +
rh + ![]() r2
r2
= ![]() rl + 2
rl + 2 ![]() rh +
rh + ![]() r2 [r1 = r]
r2 [r1 = r]
= ![]() r (l + 2h + r)
r (l + 2h + r)
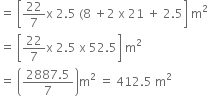
A toy is in the form of a cone mounted on a hemisphere of common base radius 7cm. The total height of the toy is 31 cm. Find the total surface area of the toy.
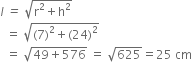
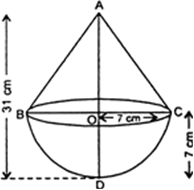
Let r1 cm be the radius of hemisphere then
r1 = 7 cm
Now, Total surface area of toy
= C.S.A of cone + C.S.A. of hemisphere
Tips: -
The interior of building is in the form of a right circular cylinder of radius 7 m and height 6 m, surmounted by a right circular cone of same radius and of vertical angle 60°. Find the cost of painting the building from inside at the rate of Rs. 30/m2.
We have, r1 = Radius of the base of the cylinder = 7m
r2 = Radius of the base of the cone = 7 m
h1 = Height of the cylinder = 6m
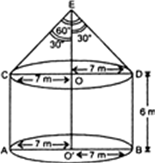
In right triangle EOC, we have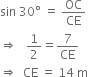
Thus, slant height (CE) = 14 m
Now,Surface area of building = Curved surface area of cylinder + curved surface area of cone![]()
Cost of painting the building from inside at the rate of Rs. 30/m2
= Rs. (572 x 30) = Rs. 17160.
A solid is composed of a cylinder with hemispherical ends. If the whole length of the solid is 100 cm and the diameter of the hemispherical ends is 28 cm, find the cost of polishing the surface of the solid at the rate of 5 paise per sq. cm.
We have,
r = radius of the cylinder
= radius of hemispherical ends = 14 cm
h = height of cylinder = 72 cm
∴ Total surface area = curved surface area of the cylinder + surface areas of hemispherical ends
= (2![]() rh +2 x 2
rh +2 x 2![]() r2) cm2
r2) cm2
= 2![]() r (h + 2r) cm2
r (h + 2r) cm2
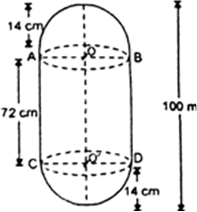
Now, cost of polishing the surface of the solid at the rate of 5 paise per sq. m
![]()
A solid toy is in the form of a hemisphere surmounted by a right circular cone. The height of the cone is 2 cm and the diameter of the base is 4 cm. Determine the volume of the toy. If a right circular cylinder circumscribes the toy.
Find the difference of the volumes of the cylinder and the toy.
(Use π = 3.14).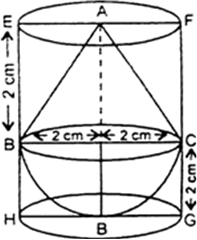
Let r cm be the radius and h cm be the height of a cone then.![]()
r1 = 2 cm, h1 = 2 cm (∵ h1= r1]
Let r2 cm be the radius and h2 cm be the height of cylinder, then
r2 = 2 cm
and h2 = (2 + 2) cm = 4 cm
Now,
Volume of solid toy,
Volume of cone + Volume of hemisphere
Volume of cylinder, 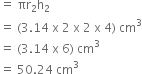
Hence,
(i) Volume of toy = 25.12 cm
(ii) Difference of the volume of cylinder and the toy
= (50.24 – 25.12) cm3
= 25.12 cm3.
An iron pole consisting of a cylindrical portion 110 cm high and base diameter 12cm is surmounted by a cone 9cm high. Find the mass of the pole it is given that 1cm3of iron has 8 gm mass.

Let r cm be the radius and h cm be the height of a cone then
r = 6 cm, h = 9 cm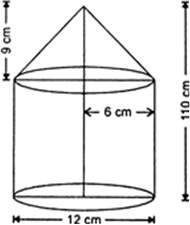

Required mass of pole
= (8 x 12780) gm = 102.240 k.g.
A tent is in the form of a cylinder surmounted by a conical top. If the height and diameter of the cylinderical part are 2.1 m and 4m respectively, and the height of the top is 2.8m, find the area of the canvas used for making the tent. Find the cost of the canvas used for making the tent. Find the cost of the canvas of the tent at the rate of Rs. 500 per m2. Also, find the volume of air enclosed in the tent.
Let ‘R’ met. be the radius and ‘H’ met. be the height of the cylindrical part.
Thus,
R = 2m and H = 2.1m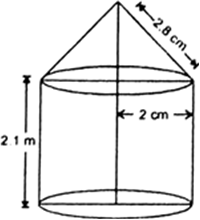
Now,
Area of the canvas used
= curved surface area of conical part + curved surface area of cylindrical part = ![]() rl + 2
rl + 2![]() RH =
RH = ![]() rl + 2
rl + 2![]() rH
rH
[∵ r = R] = ![]() r (l + 2H)
r (l + 2H)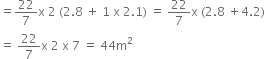
Cost of the canvas of the tent = Rs. 500 x 44 = Rs. 22,000
And.
Volume of air enclosed in the tent = Volume of the conical part + Volume of cylindrical part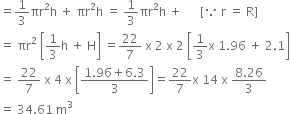
A toy is in the form of a cone mounted on a hemisphere with same radius. The diameter of the base of the conical portion is 7.0 cm and the total height of the toy is 14.5 cm. Find
the volume of the toy 
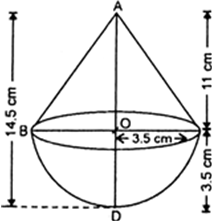
Let r cm be the radius and h cm be the height of the cone, then
r = 3.5 cm and h = 14.5 cm - 3.5 cm = 11 cm Let r1 cm be the radius of the hemisphere, then r1 = 3.5 cm
Now,
Volume of Toy
= Volume of hemisphere + Volume of cone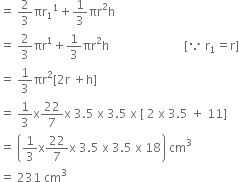
An iron pillar has lower part in the form of a right circular cylinder and the upper part in the form of a right circular cone. The radius of the base of each of the cone and cylinder is 8 cm. The cylindrical part is 240 cm high and the conical part is 36 cm high. Find the weight of the pillar if 1 cm3 of iron weighs 7.5 grams.
Let r1 and r2 cm be the radii of the base of the cylinder and cone respectively. Then, r1 = r2 = 8 cm Let h1 and h2 cm be the heights of the cylinder and the cone respectively. Then,
h1 = 240 cm and h2 = 36 cm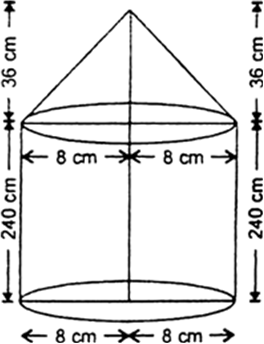
Now, Volume of the cylinder = ![]() r12h1 cm3 = (
r12h1 cm3 = (![]() x 8 x 8 x 240) cm3 = (
x 8 x 8 x 240) cm3 = (![]() x 64 x 240) cm3
x 64 x 240) cm3
Volume of the cone = 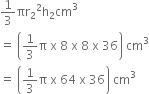
Total volume of the iron = Volume of cylinder + Volume of the cone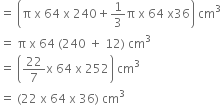
Hence, total weight of the pillar = Volume x Weight per cm3
= (22 x 64 x 36 x 7.5) = 380.16 kg
A bucket is made up of a metal sheet is in the form of a frustum of a cone of height 16cm with radii of its lower and upper ends at 8cm and 20cm respectively. Find the cost of the bucket, if the cost of metal sheet used is Rs. 15 per 100 cm2.
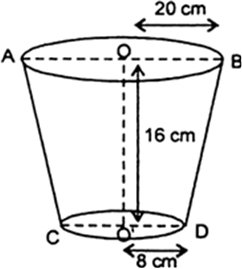
Let R and r be respectively the radii of bigger and smaller ends of the frustum
Then, R = 20 cm and r = 8 cm
Let h and l be the height and slant height of frustum, then
h = 16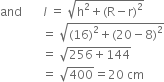
Now,
Curved surface area of the frustum
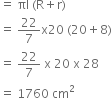
Total metal sheet required
= C. S. A. + Area of base
![]()
= 1760 + 201.14
= 1961.14 cm2
Cost of metal sheet used
![]()
= Rs 294.17
The height of a cone is 30 cm. A small cone is cut off at the top by a plane parallel to the base. If its volume be 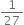 of the volume of the given cone, at which height above the base is the section made?
of the volume of the given cone, at which height above the base is the section made?
Let r and R be respectively the radii of smaller and bigger cone and h and H be their respective heights.
Now, Volume of smaller cone =
and Volume of given cone =
It is given that :
Volume of smaller cone

Hence, height of the frustum
= 30 cm - 10 cm
= 20 cm
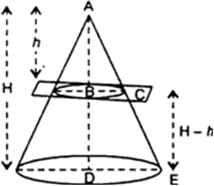
A hollow cone is cut by a plane parallel to the base and the upper portul is removed. If the curved surface of the remainder is  of the curved surface of the whole cone, find the ratio of the line-segment into which the cones altitude is divided by the plane.
of the curved surface of the whole cone, find the ratio of the line-segment into which the cones altitude is divided by the plane.
Let r and R be respectively the radii of upper portion of cone and whole cone, and h and H be their respective heights.
And let l and L be respectively the slant heights of upper portion of cone and whole cone.
It is given that :
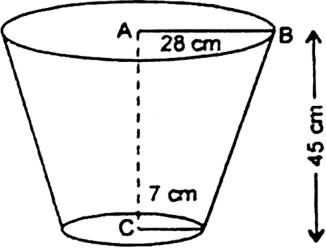
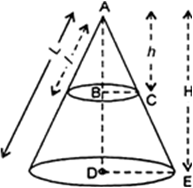
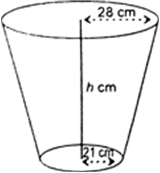
If the radii of the circular ends of a conical bucket, which is 16 cm high, are 20 cm and 8 cm, find the capacity and total surface area of the bucket.
Let R and r be the radii of top of bottom circular ends of a conical bucket, respectively and ‘h’ be the height of the bucket.
∴ h =16 cm, R = 20 cm,
r = 8 cm
Capacity of the conical bucket = Volume of the bucket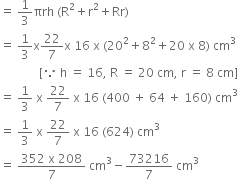
= 10459.428 cm3
= 10459.43 cm3
Slant height of the bucket is given by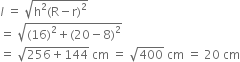
Total surface area of the conical bucket
= Curved surface area of the conical bucket
+ Area of the bottom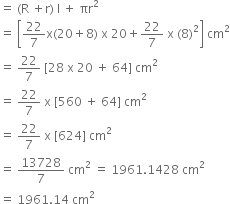
A bucket is in the form of a frustum of a cone and holds 28.49 litres of milk. The radii of the top and bottom are 28 cm and 21 cm. Find the height of the bucket.
Let ‘R’ be the radius ‘r’ be the bottom of the frustum of cone. Then,
R = 28 cm, r = 21 cm.
let ‘h’ cm be the height of the frustum of a cone.
Now,
Volume of frustum of cone = (28.49 x 1000) cm3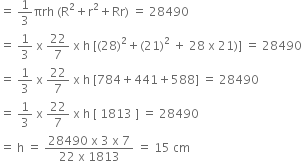
Hence, Height of bucket = 15 cm.
A bucket of height 8 cm made up of copper sheets is in the form of frustum of a right circular cone with radii of its lower ends as 3 cm and 9 cm respectively. Calculate
(i) the height of the cone of which the bucket is a part.
(ii) the volume of water which can be filled in the bucket.
(iii) the area of copper sheet required to make the bucket.
h = 8 cm, r = 3 cm and R = 9 cm
(i) Let h1 be the height of the cone of which the bucket is a part. Then,
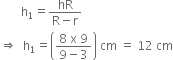
(ii) Volume of the water which can be filled in the bucket
= Volume of the frustum
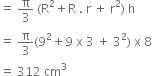
(iii) Area of the copper sheet required to make the bucket
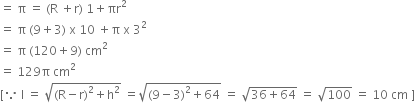
A container (open at the top) made up of a metal sheet is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm respectively. Find
(i) the cost of milk when it is completely filled with milk at the rate of Rs. 15 per litre.
(ii) the cost of metal sheet used, if it costs Rs. 5 per 100 cm2. (Take π = 3.14)
Let l be the slant height of the frustum. We have r = 8 cm,
R = 20 cm and h = 16 cm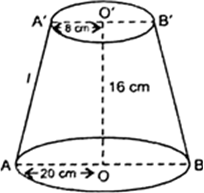
Now, volume of the container
![]() Volume of container = 10449.92 cm3
Volume of container = 10449.92 cm3![]() Volume of container =
Volume of container = ![]()
![]() Volume of container = 10.44992 litres
Volume of container = 10.44992 litres
= 10.45 litres (Approx)
∴ Cost of milk at the rate of Rs. 15 per litre = Rs.
(10.45 x 15) = Rs. 156.75
Now, Total surface area of the frustum = π (R + r) l + ![]() r2
r2
= {3.14 (20 + 8) x 20 + 3.14 x 82} cm2
= 3.14 x (560 + 64) cm3
= (3.14 x 624) cm3 = 1959.36 cm2![]() Cost of metal used = Rs.
Cost of metal used = Rs. ![]()
= Rs. 97.96 (Approx)
An open container made up of a metal sheet is in the form of a frustum of a cone of height 8 cm with radii of its lower and upper ends as 4 cm and 10 cm respectively.
Find the cost of oil which can completely fill the container at the rate of Rs. 50 per litre. Also, find the cost of metal used, if it costs Rs. 5 per 100 cm2 (Use π = 3.14).
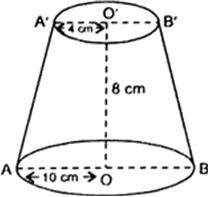
Let ‘l’ be the slant height of the frustum.
We have, R = 10 cm, r = 4 cm and h = 8 cm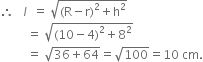
Now, volume of container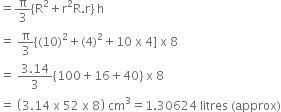
∴ Cost of oil at the rate of Rs. 50 per litre
= Rs. (1.30624 x 50) = Rs. 65.312.
Now, Total surface area of frustum
= ![]() (R + r) l +
(R + r) l + ![]() r2 [∵ Top is open]
r2 [∵ Top is open]
= 3.14 (10 + 4) (10) + 3.14 (4) (4)
= 3.14 x 140 + 3.14 x 16
= 3.14 (140 + 16) = 3.14 x 156 = 489.84 cm2
Thus the cost of metal used
![]() = Rs. 24.49 (Approx).
= Rs. 24.49 (Approx).
A bucket made up of a metal sheet is in the form of a frustum of a cone of height 16 cm with diameters of its lower and upper ends as 16 cm and 40 cm respectively. Find the volume of the bucket. Also find the cost of the bucket if the cost of metal sheet used is Rs. 20 per 100 cm2. (Use ![]() = 3.14)
= 3.14)
Let R and r be respectively the radii of bigger and smaller ends of the frustum
Then, R = 20 cm and r = 8 cm
Let h and l be the height and slant height of frustum, then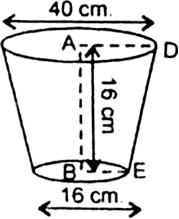
h = 16 cm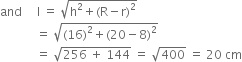
Now, Curved surface area of thefrustum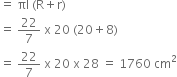
Total metal sheet required
= C.S.A. + Are of base
= 1760 + ![]() x 8 x 8
x 8 x 8
= 1760 + 201.14 = 1961.14 cm2
Cost of metal sheet used
= 1961.14 x ![]()
= Rs. 383.23 (Approx)
From a solid cylinder whose height is 8 cm and radius 6 cm, a conical cavity of height 8 cm and of base radius 6 cm, is hollowed out. Find the volume of the remaining solid correct to two places of decimals. Also find the total surface area of the remaining solid.
(Take π = 3.1416).
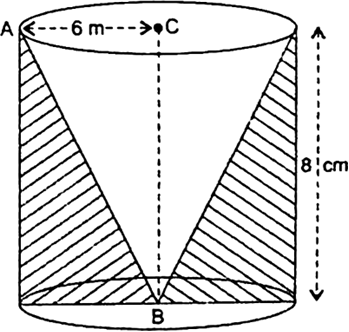
Slant height of the cone
Now, total surface area of the remaining solid
= Curved surface area of the cylinder +
area of the base of the cylinder + curve
surface area of the cone
= (2![]() x 6 x 8 +
x 6 x 8 + ![]() x 62 +
x 62 + ![]() x 6 x 10) cm2
x 6 x 10) cm2
= (96 ![]() + 36
+ 36 ![]() + 60
+ 60![]() ) cm2
) cm2
= 192![]() 192 x 3.1416
192 x 3.1416
= 603.1872 = 603.19 cm3
A bucket is in the form of a frustum of a cone with a capacity of 12308.8 cm3. The radii of the top and bottom circular ends of the bucket are 20 cm and 12 cm respectively. Find the height of the bucket and also the area of metal sheet used in making it. (Use  = 3.14)
= 3.14)
Radius of frustum,
r = 12 cm, R = 20 cm, V = 12308.8 cm3.

A toy is in the form of a cone mounted on a hemisphere of radius 3.5 cm. If the total height of the toy is 15.5 cm. Find the total surface area.

Solution not provided.
Ans. 214 cm2
An iron pole consisting of a cylindrical portions 110 cm high and of base diameter 12 cm is surmounted by a cone 9 cm high. Find the total surface area of the pole.

Solution not provided.
Ans. 4352.2 cm2
A tent is in the shape of a right circular cylinder up to a height of 3 metres and then becomes a right circular cone with a maximum height of 13.5 m above the ground. Calculate the cost of painting the inner side of the tent at the rate of Rs. 2 per sq. metre, if the radius of base is 14 m.
Solution not provided.
Ans. Rs. 2068
An iron pillar has some part in the form of a right circular cylinder and remaining in the form of a right circular cone. The radius of base of each of cone and cylinder is 8 cm. The cylindrical part is 240 cm high and the conical part is 36 cm high. Find total surface area.

Solution not provided.
Ans. 12996.3 cm2
A tent is in the form of a right circular cylinder surmounted by a cone. The diameter of the cylinder is 24 m. The height of the cylindrical portion is 11 m while the vertex of the cone is 16 m above the ground. Find the area of the canvas required for the tent.
Solution not provided.
Ans. 1320 m2
Rasheed got a playing top (lattu) as his birthday present, which surprisingly had no colour on it. He wanted to colour it with his crayons. The top is shaped like a cone surmounted by a hemisphere given in Fig. The entire top is 5 cm in height and the diameter of the top is 3.5 cm. Find the area he has to colour.
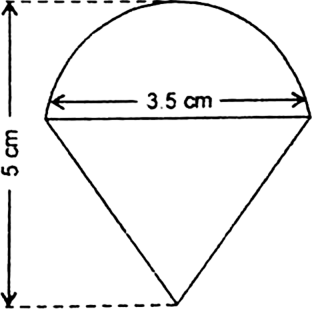
Solution not provided.
Ans. 39.6 cm2
A solid is in the form of a cylinder with hemispherical ends. The total height of the solid is 19 cm and the diameter of the cylinder is 7 cm. Find the total surface area of the solid.
Solution not provided.
Ans. 641.66 cm2
A toy is in the form of a cone mounted on a hemisphere. The diameter of the base of the cone is 18 cm and its height is 12 cm. Calculate the surface area of the toy.

Solution not provided.
Ans. 932.58 cm2
A circus tent is in the form of a right circular cylinder and a right circular cone above it. The diameter and the height of the cylindrical part of the tent are 126 m and 15 m respectively.
The total height of the tent is 21 m Find the total surface area of the tent.

Solution not provided.
Ans. 18473.4 cm2
A solid is composed of a cylinder with hemispherical ends. If the whole length of the solid is 98 cm and the diameter of each of its hemispherical ends is 28 cm, find the cost of polishing the surface area of the solid at the rate of 15 paise per sq. cm.

Solution not provided.
Ans. Rs. 1293.60
A right triangle with sides 3 cm and 4 cm is revolved around its hypotenuse. Find the surface area of double cone thus generated.
Solution not provided.
Ans. Rs. 1293.60
A circus tent consists of a cylindrical base surmounted by a conical roof. The radius of the cylinder is 20 m. The heights of the cylindrical and conical portions are respectively 42 m and 14 m. Find the capacity of the tent and also the number of persons it can
accommodate if each man is allowed  of space.
of space.
Solution is not provided.![]()
A cylindrical boiler, 4 m high and 3.5 in diameter, has a hemispherical lid. Find the volume of the interior of the boiler, including the part covered by the lid.
Solution is not provided.
Ans. 49.7 m3
A cylindrical iron pillar 42 dm high and 5 dm in radius is surmounted by a cone 7 dm high. Find the weight of the iron pillar, if 1 dm3 of iron weighs 9.6 gm.
Solution is not provided.
Ans. 33 kg 440 gm.
If the radii of the circular ends of a bucket 45 cm high, are 28 cm and 7 cm (as shown in Fig.). Find the capacity of the bucket.
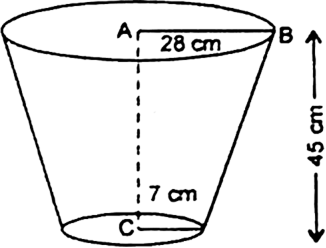
Solution not provided.
Ans. 48510 cm3
A bucket is in the form of a frustum of a cone. Its depth is 24cm and the diameters of the both ends are 30 cm and 10 cm respectively. Find the capacity of the bucket.
Solution not provided.
Ans. 8171.43 cm3
A solid right circular cone of base radius 6 cm and height 12 cm is made of metal. A right circular cone of height 4 cm is removed from eight cone leaving a pasture.
Calculate :
(i) Radius of right circular cone which has been resourved.
(ii) Volume of the frustum.
(iii) Whole surface area of frustum.
Solution not provided.
Ans. (i) 2 cm (ii) 435.8 cm3 (iii) 350.58 cm2
A tent consists of frustum of a right circular cone capped by a right circular cone. Find the area of canvas required for the tent. The radii of the ends of the frustum are 15 cm and 9 cm. The height of the frustum is 8 cm and slant height of conical cone is 10 cm.
Solution not provided.
Ans. 330 cm2
The perimeters of the ends of a frustum of a right circular cone are 44 cm and 33 cm. If the height of the frustum be 16 cm, find it volume, the slant surface and the total surface.
Solution not provided.
Ans. 1900 cm3, 620 cm2, 860.625 cm2
A bucket made up of a metal sheet is in the form of frustum of a cone. Its depth is 24cm and the diameters of the top and bottom are 30 cm and 10 cm respectively. Find the cost of milk which can completely fill the bucket at the rate of Rs. 20 per litre and the cost of metal sheet used if it costs Rs. 10 per 100 cm2. [Use  = 3.14]
= 3.14]
Solution not provided.
Ans. Rs. 163.28, 171.13
A cone of radius 10 cm is divided into two parts by drawing a plane through the mid-point of its axis, parallel to its base. Compare the volumes of the two parts.
Solution not provided.
Ans. 204.28 m2
An open metallic bucket is in the shape of a frustum of a cone mounted on hollow cylindrical base made of metalic sheet. It the diameters of the two circular ends of the bucket are 45 cm and 25cm, the total vertical height of the bucket is 30 cm and that of the cylindrical portion is 6 cm. Find the area of the metallic sheet used to make the bucket. Also find the volumes of water it can hold, [Take  = 22/7]
= 22/7]
Solution not provided.
Ans. 23.73 litres
A bucket is in the form of a frustum of a cone with a capacity of 12308.8 cm3 of water. The radii of the top and bottom circular ends are 20 cm and 12 cm respectively. Find the height of the bucket and the area of the metal sheet used in making. [Use  = 3.14]
= 3.14]
Solution not provided.
Ans. 2160.32 cm3
A solid is in the form of a circular cone mounted on a hemisphere. The radius of the hemisphere Rs. 2.1 cm and the height of the cone is 4cm. The solid is placed in a cylindrical tub full of water in such a way that the whole solid is submerged in water. If the radius of the cylinder is 5cm and its height is 9.8 cm. Find the volume of the water left is the cylinderical tub.
Solution not provided.
Ans. 732.166 cm3
An open metallic bucket is in the shape of a frustum of a cone mounted on hollow cylindrical base made of metallic sheet. If diameters of the circular ends of the bucket are 45 cm and 25 cm, the total vertical height of the bucket is 40 cm and that of the cylinderical portion is 6 cm. Find the area of metallic sheet used to make the bucket. Also, find the volume of water it hold. [Take  = 22/7]
= 22/7]
Solution not provided.
Ans. 0.7724 litres
A lead pencil consist of a cylinder of wood with a solid cylinder of graphite filled into it. The diameter of the pencil is 7 mm, the diameter of the graphite is 7 mm and the length of the pencil is 10 cm. Calculate the weight of the whole pencil, if the specific gravity of the wood is 0.7 gm/cm3 and the graphite is 2.1 gm/cm3.
Solution not provided.
Ans. 2805 gm
A godown building is in the form as shown in Fig. 13.52. The vertical cross-section parallel to the width side of the building is a rectangle 7 m x 3 m, mounted by a semicircle of radius 3.5 m. The inner measurements of the cuboidal portion of the building are 10 m x 7 m x 3 m. Find the volume of the godown and the totel interior surface area excluding the floor (base).
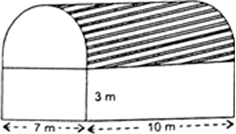
Solution not provided.
Ans. 402.5 m3 ; 250.5 m3
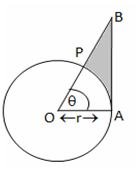
In fig. O is the centre of the bigger circle and AC is its diameter. Another circle with AB as diameter is drawn. If AC = 54 cm and BC = 10 cm, find the area of the shaded region.
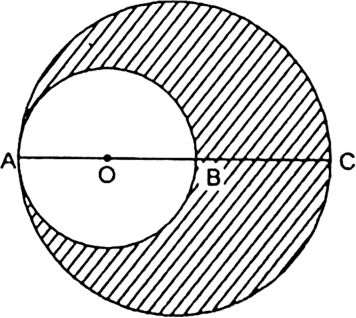
Solution is not provided.
Ans. 770 cm2
A toy is in the form of a cone mounted on a hemisphere of radius 3.5 cm. If the total height of the toy is 15.5 cm, find its total surface area. 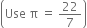
Solution is not provided.
Ans. 214.5 cm2
In fig. AB is a diameter of the circle with centre O and OA = 7 cm. Find the area of the shaded region 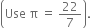

Solution is not provided.
Ans. 66.5 cm2
If the radii of the circular ends of a conical bucket, which is 45 cm high, are 28 cm and 7
cm, find the capacity of the bucket, 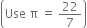
Solution is not provided.
Ans. 48510 cm3
A cylindrical tub of radius 5 cm and length 9.8 cm is full of water. A solid in the form of a right circular cone mounted on a hemisphere is immersed into the tub. If the radius of the hemisphere is 3.5 cm and height of cone outside the hemisphere is 5 cm, find the volume of water left in the tub (Take  = 22/7).
= 22/7).
Solution is not provided.
Ans. 616 cm3
A toy is in the form of a cone mounted on a hemisphere of diameter 7 cm The total height of the toy is 14.5 cm. Find the volume and the total surface area of the toy. (Take  = 22/7).
= 22/7).
Solution is not provided.
Ans. 243.8 cm3, 204.05 m3
The minute hand of a clock is 12 cm long. Find the area on the face of the clock described by the minute hand in 35 minutes ( = 22/7).
= 22/7).
Solution is not provided.
Ans. 264 cm2
A sector of a circle of radius 15 cm has the angle 120°. It is rolled up so that two bounding radii are joined together to form a cone. Find the volume of the cone 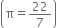 .
.
Solution is not provided.
Ans. 370.33 cm2
A chord AB of a circle of radius 10 cm makes a right angle at the centre of the circle. Find the area of the major and minor segments. (Take  = 3.14).
= 3.14).
Solution is not provided.
Ans. 28.5 cm2, 285.5 cm2
A rectangle 8 cm x 6 cm is inscribed in a circle as shown in figure. Find the area of the shaded region (use  = 3.14).
= 3.14).
Solution not provided.
Ans. 30.5 cm2
A chord AB of a circle of radius 14 cm makes a right angle at the centre (O) of the circle. Find the area of the miner segment (Take π = 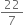 )
)
Solution not provided.
Ans. 56 cm2
A toy is in the shape of a right circular cylinder with a hemisphere on one end and a cone on the other. The radius and height of the cylindrical part are 5 cm, 13 cm respectively. The radii of the hemispherical and conical parts are the same as that of the cylindrical part. Find the surface area of the toy, if the total height of the toy is 30 cm.
Solution not provided.
Ans. 770 cm2
The internal and external radii of a hollow sphere are 3 cm and 5 cm respectively. The sphere is melted to form a solid cylinder of height 22/3 cm. Find the diameter and curved surface area of the cylinder.
Solution not provided.
Ans. 14 cm, 117.33 cm3
A right triangle with sides 3 cm and 4 cm is revolved around its hypotenuse. Find the volume of the double cone thus generated.
Solution not provided.
Ans. 30.17 cm3
A solid metallic sphere of diameter 21 cm is melted and recasted into a number of smaller cones, each of diameter 7 cm and height 3 cm. Find the number of cones so formed.
Solution not provided.
Ans. 126 cones
A solid metallic sphere of diameter 28 cm is melted and recasted into a number of smaller cones, each of diameter  cm and height 3 cm. Find the number of cones so formed.
cm and height 3 cm. Find the number of cones so formed.
Solution not provided.
Ans. 672 cones
A solid metallic sphere of diameter 21 cm is melted and recast into a number of smaller cones, each of diameter 3.5 cm and height 3 cm. Find the number of cones so formed.
Solution not provided.
Ans. 503 cones
A hollow cone is cut by a plane parallel to the base and upper portion is removed. If the curved sarface of the remainder is 8/9 of the curved surface of the whole cone, find the ratio of the line segments into which the altitude of the cone is divided by the plane.
Solution not provided.
Ans. 1 : 2
A toy is in the form of a cone mounted on a hemisphere of radius 3.5. cm. The total height of the toy is 15.5. Find the total surface area of the toy. (use  = 22/7)
= 22/7)
Solution not provided.
Ans. 214.5 cm2
If the radii of the circular ends of a bucket, 45cm high are 28 cm and 7 cm respectively. Find the capacity of the bucket.
Solution not provided.
Ans. 48510 cm3
50 circular plates, each of radius 7 cm, and thickness 1/2 cm, are placed one above the other to form a solid right circular cylinder. Find the total surface area and volume of the cylinder so formed, (use  = 22/7)
= 22/7)
Solution not provided.
Ans. 1408 cm2, 3850 cm3
The radii of circular ends of a solid frustum of a cone are 33 cm and 27 cm and its slant height is 10 cm. Find its total surface area.
Solution not provided.
Ans. 7599.43 cm2
A tent is in the form of a cylinder of diameter 4.2 m and height 4 m surmoun-ted by a cone at equal base and height 2.8 m. Find the capacity of the tent and the cost of canvas for making the tent at Rs. 100 per sq. m.
Solution not provided.
Ans. 68.376 cm3, Rs. 7,590
It the radii of the ends of a bucket, 45 cm high, are 28 cm and 7 cm, determine total surface area of the bucket.
Solution not provided.
Ans. 561.6 cm3
A solid cylinder of diameter 12 cm and height 15 cm is melted and recast into 12 toys in the shape of a right circular cone mounted on a hemisphere. Find the radius of the hemisphere and the total height of the toy if height of the conical part is 3 times its radius.
Solution not provided.
Ans. 3 cm
The rain water from a roof 22 m x 20 m drains into a cylindrical vessel having diameter of base 2 m and height 3.5 m. If the vessel is just full, find the rainfall in cm.
Solution not provided.
Ans. 2.5 cm
The rain water from a roof 22 m x 20 m drains into a cylindrical vessel having diameter of base 2 m and height 3.5 m. If the vessel is just full, find the rainfall in cm.
Solution not provided.
Ans. Rs. 293.90 (approx.)
A bucket made up of a metal sheet is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm respectively. Find the cost of the bucket if the cost of metal sheet used is Rs. 15 per 100 cm2 (use  = 3.14).
= 3.14).
Solution not provided.
Ans. Rs. 293.90 (approx.)
A bucket made up of a metal sheet is in the form of a frustum of a cone. Its depth is 24 cm and the diameters of the top and bottoms are 30 cm and 10 cm respectively. Find the cost of milk which can completely fill the bucket at the rate of Rs. 20 per litre and the cost of the metal sheet used, if it costs Rs. 10 per 100 cm2 (use  = 22/7).
= 22/7).
Solution not provided.
Ans. Rs. 163,28, Rs. 171.13
A toy is in the form of a cone mounted on a hemisphere of common base radius 7 cm. The total height of the toy is 31 cm. Find the total surface area of the toy.
Solutionn not provided.
Ans. 858 cm3
In given fig. find the perimeter of shaded region where ADC, AEB and BFC are semi-circle on diameters AC, AB and BC respectively.
Solutionn not provided.
Ans. 13.2 cm
Find the area of the shaded region in the given figure, where ABCD is a square of side 14 cm.
Solutionn not provided.
Ans. 42 cm2
A gulab jamun, when ready for eating, contain sugar syrup of about 30% of its volume. Find approximately how much syrup would be found in 45 such gulab jamus, each shaped like a cylinder with two hemispherical ends, if the complete length of each of the m is 5cm and its diameter is 2.8 cm.
Solutionn not provided.
Ans. 338 cm3 (app.)
A bucket made up of a metal sheet is in the formal a frustum of a cone of height 16 cm with diameters of its lower and upper ends as 16 cm and 40 cm respectively. Find the volume of the bucket . Also find the cost of the bucket if the cost of metal sheet used is Rs. 20 per 100 cm2. (Use  = 3.14)
= 3.14)
Solutionn not provided.
Ans. 10449.92 cm3, Rs. 391.87
A tent consists of frustum of a cone surmounted by a cone. If the diameters of the upper and lower circular ends of the frustrum be 14m and 26m respectively, the height of the frustum be 8m and the slant height of the surmounted conical portion be 12m, find the area of canvas required to make the tent. (Assume that the radii of the upper circular end of the frustum and the base of surmounted conical portion are equal)
Solutionn not provided.
Ans. 892.57 m2
The length of a minor arc is  of the circumference of the circle. Write the measure of the angle subtended by the arc of the centre of the circle.
of the circumference of the circle. Write the measure of the angle subtended by the arc of the centre of the circle.
Solutionn not provided.
Ans. 80
In the given Fig., the shape of the top of a table in a restaurant is that of a sector of a circle with centre O.
(i) the area of the top of the table. (ii) the perimeter of the table top.
Solutionn not provided.
Ans. (i) 9078 cm2, (ii) 402.6 cm.
A spherical copper shell of external diameter 18 cm is melted and recast into a solid cone of base radius 14 cm and height  cm. Find the inner diameter of the shell.
cm. Find the inner diameter of the shell.
Solutionn not provided.
Ans. 16 cm
A bucket is in the form of a frustrum of a cone with cavity of 12308.8 cm3. The radii of the top and bottom circular ends of the bucket are 20 cm and 12 cm respectively. Find the height of the bucket and also the area of metal used in making it.
Solutionn not provided.
Ans. 15 cm, 2160.32 cm2
A juice seller serves his customers using a glass as shown in given Fig. The inner diameter of the cylindrical glass is 5 cm, but the bottom of the glass has a hemispherical portion raised which reduces the capacity of the glass. If the height of the glass is 10 cm. Find the apparent capacity of the glass and its actual capacity. [Use  = 3.14]
= 3.14]
Solutionn not provided.
Ans. 196.25 cm3; 163.54 cm3
A cylindrical vessel, with internal diameter 10 cm and height 10.5 cm, is full of water. A solid cone of base diameter 7 cm and height 6 cm is completely immersed in water. Find the volume of
(i) Water displaced out of the cylinderical vessel,
(ii) Water left in the cylindrical vessel.
Solutionn not provided.
Ans. 748 cm3
If the diameter of a semicircular protector is 14 cm. Find its perimeter.
Solutionn not provided.
Ans. 36 cm.
In Fig., a tent is in the shape of a cylinder surmounted by a conical top of the same diameter. If the height and diameter of cylindrical part are 2.1 m and 3 m respectively and the slant height of conical part is 2.8 m, find the cost of canvas needed to make the tent if the canvas is available at the rate of Rs. 500/sq. metre. (use π = 22/7)
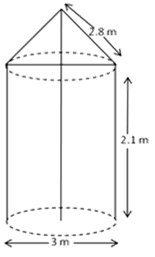
In Fig., a tent is in the shape of a cylinder surmounted by a conical top of the same diameter. If the height and diameter of cylindrical part are 2.1 m and 3 m respectively and the slant height of conical part is 2.8 m, find the cost of canvas needed to make the tent if the canvas is available at the rate of Rs. 500/sq. metre. (use π = 22/7)
In the given figure,
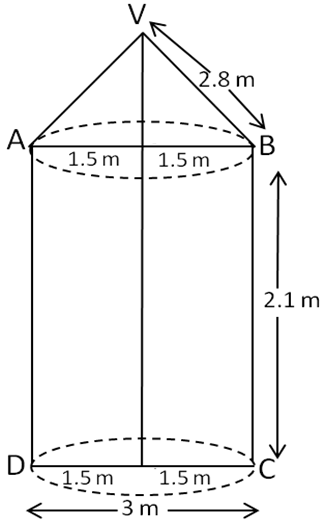 Given diameter 3m
Given diameter 3mFor conical portion,
radius = 3/2 = 1.5m and length is 2.8m
∴ S1 = curved surface area of conical portion
∴ S1 = πrl
= π x 1.5 x 2.1
= 6.3π m2
Area of canvas used for making tent = S1+S2
=4.2π +6.3π
= 10.5π
=10.5 x (22/7)
=33m2
Thus, total cost of the canvas at the rate of Rs. 500 per m2 = 500 x 33 =16500
Rs. 16500 is total cost.
A conical vessel, with base radius 5 cm and height 24 cm, is full of water. This water is emptied into a cylindrical vessel of base radius 10 cm. Find the height to which the water will rise in the cylindrical vessel. (π = 22/7)
Let the radius of the conical vessel = r1 = 5 cm
Height of the conical vessel = h1 = 24 cm
Radius of the cylindrical vessel = r2
Let the water rise upto the height of h2 cm in the cylindrical vessel.
Now, volume of water in conical vessel = volume of water in cylindrical vessel

A sphere of diameter 12 cm, is dropped in a right circular cylindrical vessel, partly filled with water. If the sphere is completely submerged in water, the water level in the cylindrical vessel rises by ![]() . Find the diameter of the cylindrical vessel.
. Find the diameter of the cylindrical vessel.
Given,
Diameter of sphere 12 cm,
therefore radius of sphere is 12/2 = 6 cm

Due to heavy floods in a state, thousands were rendered homeless. 50 schools collectively offered to the state government to provide the place and the canvas for 1500 tents to be fixed by the governments and decided to share the whole expenditure equally. The lower part of each tent is cylindrical of base radius 2.8 cm and height 3.5 m, with conical upper part of same base radius but of height 2.1 m. If the canvas used to make the tents costs Rs. 120 per sq. m, find the amount shared by each school to set up the tents. What value is generated by the above problem? (Use π = 22/7)
Given,
Height of conical upper part = 3.5m,
radius = 2.8 m
(slant height of cone)2 = (2.1)2 +(2.8)2 = 4.41+7.84
(Slant height of cone)2 = ![]()
the canvas used for each tent
= curved surface area of cylinder base+curved surface area of conical upper part

Due to sudden floods, some welfare associations jointly requested the government to get 100 tents fixed immediately and offered to contribute 50% of the cost. If the lower part of each tent is of the form of a cylinder of diameter 4.2 m and height 4 m with the conical upper part of same diameter but of height 2.8 m, and the canvas to be used costs Rs. 100 per sq. m, find the amount, the associations will have to pay. What values are shown by these associations? [ use π = 22/7]
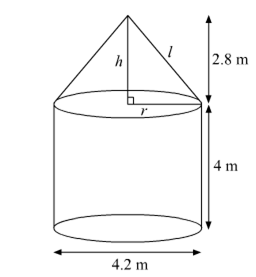
Height of the cylindrical part, H = 4 m
Height of the conical part, h = 2.8 m
Radius of the base, r = 2.1 m

Cost of the canvas = Rs 100/ m2
So, total cost of the canvas to be used = 75.9 x 100 = Rs 7,590
Amount that the association will have to pay for each tent
=50% of Rs 7590
= Rs (50/100) x 7590
= Rs 3,795
Therefore, Amount that the associations will have for 100 tent = Rs 3795 x 100
= Rs 379500
Hence, the amount that the associations will have to pay for 100 tents is Rs 3,79,500
The associations are showing humanity and their helpful nature.
A hemispherical bowl of internal diameter 36 cm contains liquid. This liquid is filled into 72 cylindrical bottles of diameter 6 cm. Find the height of the each bottle, if 10% liquid is wasted in this transfer.
Radius of each cylindrical bottle, R = 6/2 = 3 cm
volume of each cylindrical bottle = πR2h
= π x 3 x3 x h
Therefore, Total volume of 72 such cylindrical bottles
= π x 3 x3 x h x 72
= 648 πh2 cm3
According to the question,
Total volume of 72 such cylindrical bottles = volume of the liquid transferred
Therefore, 648 πh = 3499.2π
⇒ h = 3499.2/648
⇒ h = 5.4 cm
Hence, the height of each cylindrical bottle is 5.4 cm
A cubical block of side 10 cm is surmounted by a hemisphere. What is the largest diameter that the hemisphere can have ? Find the cost of painting the total surface area of the solid so formed, at the rate of Rs 5 per 100 sq. cm. [Use π =3.14]
Now,
Total surface area of the solid = Total surface area of the cube + curved surface area of the hemisphere - Area of the base of the hemisphere
= 6a2 + 2πr2 -πr2
= [ 6 x (10)2 + 2 x 3.14 x (5)2 - 3.14 x (5)2] cm2
= (600 +157 -78.5 ) cm2
= 678.5 cm2
Cost of painting = Rs 5 per 100 cm2
Therefore,
Cost of painting the solid = 678.5 x (5/100) = Rs. 33.90
Hence, the approximate cost of painting the solid so formed is Rs. 33.90
504 cones, each of diameter 3.5 cm and height 3 cm, are melted and recast into a metallic sphere. Find the diameter of the sphere and hence find its surface area. [Use π =22/7]
Given,
Diameter of the cone = 3.5 cm
∴ Radius of the cone, r= 3.5 /2 cm
Height of the cone, h = 3 cm
Now,
Let the radius of metallic sphere be R
It is given that cones are melted and recast into a metallic sphere.
therefore the volume of the sphere = Volume of 504 cones

In Figure, PQRS is a square lawn with side PQ = 42 metres. Two circular flower beds are there on the sides PS and QR with centre at O, the intersection of its diagonals. Find the total area of the two flower beds (shaded parts).
Area of the square lawn PQRS = 42 m x 42 m
Let OP = OS = xm
So, x2 + x2 = (42)2
⇒ 2x2 = 42 x 42
⇒ x2 = 21 x 42
Now,
area of sector POS=
From each end of a solid metal cylinder, metal was scooped out in the hemispherical form of the same diameter. The height of the cylinder is 10 cm and its base is of radius 4.2 cm. The rest of the cylinder is melted and converted into a cylindrical wire of 1.4 cm thickness. Find the length of the wire. ( π = 22/7)
Height of the solid metal cylinder, h = 10 cm
Radius of the solid metal cylinder, r = 4.2 cm
therefore,
Radius of each hemisphere = radius of the solid metal cylinder, r = 4.2 cm
Now,
Volume of the rest of the cylinder = Volume of cylinder - 2 x volume of each hemisphere
Thickness of the cylindrical wire = 1.4 cm
Therefore,
Radius of the cylindrical wire, R = 1.4/2 = 0.7 cm
Let the length of the wire be H cm.
It is given that the rest of the cylinder is melted and converted into a cylindrical wire.
therefore,
Volume of the cylindrical wire = Volume of the rest of the cylinder
⇒ π x 0.7 x 0.7 x H = π x (4.2)2 x (4.4)
![]()
Hence, the length of the wire is 158.4 cm
The table below shown the salaries of 280 persons:
| Salary (In thousand) | No. of Person |
| 5-10 | 49 |
| 10-15 | 133 |
| 15-20 | 63 |
| 20-25 | 15 |
| 25-30 | 6 |
| 30-35 | 7 |
| 35-40 | 4 |
| 40-45 | 2 |
| 45-50 | 1 |
Calculate the median salary of the data.
| Class | Frequency (F) | Cumulative Frequency (f) |
| 5 -10 | 49 | 49 |
| 10-15 | 133 | 182 |
| 15-20 | 63 | 245 |
| 20-25 | 15 | 260 |
| 25-30 | 6 | 266 |
| 30-35 | 7 | 273 |
| 35-40 | 4 | 277 |
| 40-45 | 2 | 279 |
| 45-50 | 1 | 280 |
The mean of the following distribution is 18. Find the frequency f of the class 19-21.
| Class | 11-13 | 13-15 | 15-17 | 17-19 | 19-21 | 21-23 | 23-25 |
| Frequency | 3 | 6 | 9 | 13 | f | 5 | 4 |
| Class | Mid values xi | Frequency fi | di = xi -18 | fiui | |
| 11-13 | 12 | 3 | -6 | -3 | 9 |
| 13-15 | 14 | 6 | -4 | -2 | -12 |
| 15-17 | 16 | 9 | -2 | -1 | -9 |
| 17-19 | 18 | 13 | 0 | 0 | 0 |
| 19-21 | 20 | f | 2 | 1 | f |
| 21-23 | 22 | 5 | 4 | 2 | 10 |
| 23-25 | 24 | 4 | 6 | 3 | 12 |
The following distribution gives the daily income of 50 workers of a factory:
| Daily Income (In) | 100-120 | 120-140 | 140-160 | 160-180 | 180-200 |
| Number of workers | 12 | 14 | 8 | 6 | 10 |
Convert the distribution above to a less than type cumulative frequency distribution and draw its ogive.
| Daily income | Frequency | Income less than | cumulative frequency |
| 100-120 | 12 | 120 | 12 |
| 120-140 | 14 | 140 | 26 |
| 140-160 | 8 | 160 | 34 |
| 160-180 | 6 | 180 | 40 |
| 180-200 | 10 | 200 | 50 |
Mock Test Series
Sponsor Area
Sponsor Area