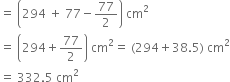A cubical block of side 7 cm is surmounted by a hemisphere. What is the greatest diameter the hemisphere can have? Find the surface area of the solid.

Solution

Let a be the length of an edge of the cube. Then
a = 7 cm
Greatest diameter of the hemisphere
= Length of an edge of the cube
= 7 cm
Now,
Surface area of the cube
= 6 (edge)²= 6 x 7²= 6 x 49 = 294 cm²Let r be the radius of the hemisphere.
Then, r = $7 over 2 space cm$
Now,
Curbed surface area of hemisphere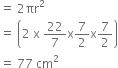
$WiredFaculty$
And, Base area = $WiredFaculty$
$space space space equals space space 77 over 2 space cm squared$
Total surface area
= Surface area of the cube + curved surface area of the hemisphere – base area of the hemisphere
$WiredFaculty$