Question

From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest cm².

Solution

Let r cm be the radius and h cm be the height of the cylinder, then
r = 0.7 cm and h = 2.4 cm.
Let r₁ cm be the radius, l cm be the slant height and h₁ cm be the height of the cone, then
r₁ = 0.7 cm and h₁ = 2.4 cm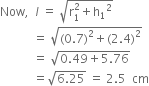
$Now comma space space l italic space equals space square root of straight r subscript 1 superscript 2 plus straight h subscript 1 squared end root space space space space space space space space space space space equals space square root of left parenthesis 0.7 right parenthesis squared plus left parenthesis 2.4 right parenthesis squared end root space space space space space space space space space space space equals space square root of 0.49 plus 5.76 end root space space space space space space space space space space space equals square root of 6.25 end root space equals space 2.5 space space cm$

Now,
Total surface area of the remaining solid
= (C.S.A of cylinder) + (C.S.A of cone) + (area of upper base of the cylinder)
= 2 π rh + πr²l + πr²= 2 π rh + π rl + π r² [ ∵ r = r₁]
$equals space open parentheses 2 space straight x space 22 over 7 space straight x space 0.7 space straight x space 2.4 space plus 22 over 7 straight x space 0.7 space straight x space 2.5 space plus space 22 over 7 straight x space 0.7 space straight x space 0.7 close parentheses space space cm squared equals space left parenthesis 1.56 space plus space 5.5 space plus 1.54 right parenthesis space cm squared equals space 17.6 space cm squared$

For Daily Free Study Material Join wiredfaculty

Statistics

From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest cm².

Some More Questions From Statistics Chapter

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

Phone Number

Email Address

Loaction

For Daily Free Study Material Join wiredfaculty

Statistics

From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest cm2.

Some More Questions From Statistics Chapter

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest cm².