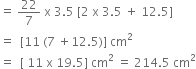Question
A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. The total height of the toy is 15.5 cm. Find the total surface area of the toy.
Solution
Let r cm be the radius, h cm be the height and l cm be the slant height of the cone, then
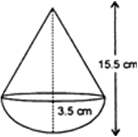

r = 3.5 cm,
h = (15.5 – 3.5) cm = 12 cm.
Now, l = 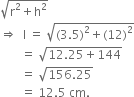
Let r1 cm be the radius of the hemisphere.
Then, r1 = 3.5 cm [∵ r = r1]
Now,
The total surface area of the toy
= CSA of hemisphere
+ CSA of cone
= 2 π r12 + πrl
= 2π r2 + πrl [ ∵ r1= r]
= π r [2r + l]
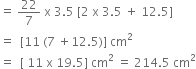
Then, r1 = 3.5 cm [∵ r = r1]
Now,
The total surface area of the toy
= CSA of hemisphere
+ CSA of cone
= 2 π r12 + πrl
= 2π r2 + πrl [ ∵ r1= r]
= π r [2r + l]