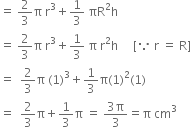Question
A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of π.
Solution
Let r cm be the radius of the hemisphere, then r = 1 cm.
Let R be the radius of the cone and h cm be the height. Then
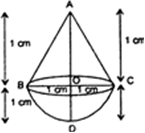
R = 1 cm and h = 1 cm
[It is given that R = h)
Now, Volume of solid
= Volume of hemisphere + volume of cone