A hemispherical depression is cut out from one face of a cubical wooden block such that the diameter l of the hemisphere is equal to the edge of the cube. Determine the surface area of the remaining solid.

Solution

It is given that,
Edge of the cube = l
Then, Surface area = 6 (edge)² = 6l²Now, the greatest diameter of hemisphere
= length of an edge of the cube
= l
So, curved surface area of the hemisphere

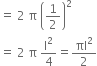
$WiredFaculty$
And, Area of base of the hemisphere

$WiredFaculty$

Required surface area
= Surface area of the cubical wooden block – area of the base of the hemisphere + curved surface area of the hemisphere
$equals space 6 l to the power of italic 2 italic minus pi over italic 4 l to the power of italic 2 italic equals italic 6 l to the power of italic 2 italic plus pi over italic 4 l to the power of italic 2$