Mathematics Chapter 7 Triangles
Sponsor Area
NCERT Solution For Class 9 About 2.html
In quadrilateral ACBD, AC = AD and AB bisects ∠A (See the given figure). Show that ΔABC ≅ ΔABD. What can you say about BC and BD?
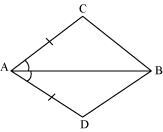
In ΔABC and ΔABD,
AC = AD (Given)
∠CAB = ∠DAB (AB bisects ∠A)
AB = AB (Common)
∴ ΔABC ≅ ΔABD (By SAS congruence rule)
∴ BC = BD (By CPCT)
Therefore, BC and BD are of equal lengths.
ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA (See the given figure). Prove that
(i) ΔABD ≅ ΔBAC
(ii) BD = AC
(iii) ∠ABD = ∠BAC.
In ΔABD and ΔBAC,
AD = BC (Given)
∠DAB = ∠CBA (Given)
AB = BA (Common)
∴ ΔABD ≅ ΔBAC (By SAS congruence rule)
∴ BD = AC (By CPCT)
And, ∠ABD = ∠BAC (By CPCT)
AD and BC are equal perpendiculars to a line segment AB (See the given figure). Show that CD bisects AB.
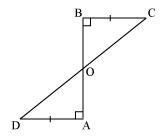
In ΔBOC and ΔAOD,
∠BOC = ∠AOD (Vertically opposite angles)
∠CBO = ∠DAO (Each 90º)
BC = AD (Given)
∴ ΔBOC ≅ ΔAOD (AAS congruence rule)
∴ BO = AO (By CPCT)
⇒ CD bisects AB.
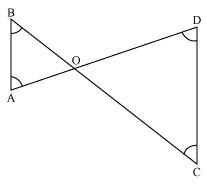
l and m are two parallel lines intersected by another pair of parallel lines p and q (see the given figure). Show that ΔABC ≅ ΔCDA.
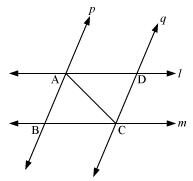
In ΔABC and ΔCDA,
∠BAC = ∠DCA (Alternate interior angles, as p || q)
AC = CA (Common)
∠BCA = ∠DAC (Alternate interior angles, as l || m)
∴ ΔABC ≅ ΔCDA (By ASA congruence rule)
Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see the given figure). Show that:
(i) ΔAPB ≅ ΔAQB
(ii) BP = BQ or B is equidistant from the arms of ∠A.
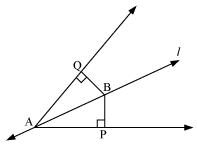
In ΔAPB and ΔAQB,
∠APB = ∠AQB (Each 90º)
∠PAB = ∠QAB (l is the angle bisector of ∠A)
AB = AB (Common)
∴ ΔAPB ≅ ΔAQB (By AAS congruence rule)
∴ BP = BQ (By CPCT)
Or, it can be said that B is equidistant from the arms of ∠A.
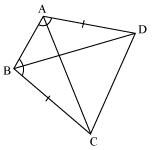
In the given figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.
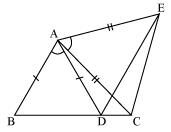
It is given that ∠BAD = ∠EAC
∠BAD + ∠DAC = ∠EAC + ∠DAC
∠BAC = ∠DAE
In ΔBAC and ΔDAE,
AB = AD (Given)
∠BAC = ∠DAE (Proved above)
AC = AE (Given)
∴ ΔBAC ≅ ΔDAE (By SAS congruence rule)
∴ BC = DE (By CPCT)
AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (See the given figure). Show that
(i) ΔDAP ≅ ΔEBP
(ii) AD = BE
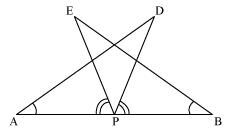
It is given that ∠EPA = ∠DPB
⇒ ∠EPA + ∠DPE = ∠DPB + ∠DPE
⇒ ∠DPA = ∠EPB
In ΔDAP and ΔEBP,
∠DAP = ∠EBP (Given)
AP = BP (P is mid-point of AB)
∠DPA = ∠EPB (From above)
∴ ΔDAP ≅ ΔEBP (ASA congruence rule)
∴ AD = BE (By CPCT)
In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O. Show that:
(i) OB = OC (ii) AO bisects ∠A
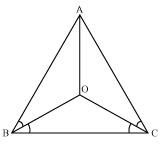
(i) It is given that in triangle ABC, AB = AC
⇒ ∠ACB = ∠ABC (Angles opposite to equal sides of a triangle are equal)
⇒ ∠ACB = ∠ABC
⇒ ∠OCB = ∠OBC
⇒ OB = OC (Sides opposite to equal angles of a triangle are also equal)
(ii) In ΔOAB and ΔOAC,
AO =AO (Common)
AB = AC (Given)
OB = OC (Proved above)
Therefore, ΔOAB ≅ ΔOAC (By SSS congruence rule)
⇒ ∠BAO = ∠CAO (CPCT)
⇒ AO bisects ∠A.
In ΔABC, AD is the perpendicular bisector of BC (see the given figure). Show that ΔABC is an isosceles triangle in which AB = AC.
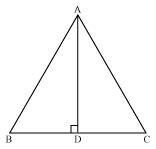
In ΔADC and ΔADB,
AD = AD (Common)
∠ADC =∠ADB (Each 90º)
CD = BD (AD is the perpendicular bisector of BC)
∴ ΔADC ≅ ΔADB (By SAS congruence rule)
∴AB = AC (By CPCT)
Therefore, ABC is an isosceles triangle in which AB = AC
ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see the given figure). Show that these altitudes are equal.
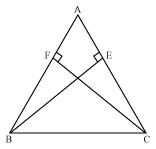
In ΔAEB and ΔAFC,
∠AEB and ∠AFC (Each 90º)
∠A = ∠A (Common angle)
AB = AC (Given)
∴ ΔAEB ≅ ΔAFC (By AAS congruence rule)
⇒ BE = CF (By CPCT)
ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see the given figure). Show that
(i) ΔABE ≅ ΔACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.
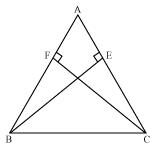
(i) In ΔABE and ΔACF,
∠AEB = ∠AFC (Each 90º)
∠A = ∠A (Common angle)
BE = CF (Given)
∴ ΔABE ≅ ΔACF (By AAS congruence rule)
(ii) It has already been proved that
ΔABE ≅ ΔACF
⇒ AB = AC (By CPCT)
ABC and DBC are two isosceles triangles on the same base BC (see the given figure). Show that ∠ABD = ∠ACD.
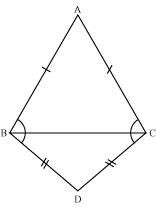

Let us join AD.
In ΔABD and ΔACD,
AB = AC (Given)
BD = CD (Given)
AD = AD (Common side)
∴ ΔABD ΔACD (By SSS congruence rule)
⇒ ∠ABD = ∠ACD (By CPCT)
ΔABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see the given figure). Show that ∠BCD is a right angle.
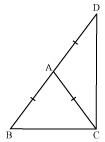
In ΔABC,
AB = AC (Given)
⇒ ∠ACB = ∠ABC (Angles opposite to equal sides of a triangle are also equal)
In ΔACD,
AC = AD
⇒ ∠ADC = ∠ACD (Angles opposite to equal sides of a triangle are also equal)
In ΔBCD,
∠ABC + ∠BCD + ∠ADC = 180º (Angle sum property of a triangle)
⇒ ∠ACB + ∠ACB +∠ACD + ∠ACD = 180º
⇒ 2(∠ACB + ∠ACD) = 180º
⇒ 2(∠BCD) = 180º
⇒ ∠BCD = 90º
ABC is a right angled triangle in which ∠A = 90º and AB = AC. Find ∠B and ∠C.
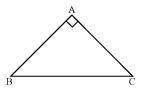
It is given that
AB = AC
⇒ ∠C = ∠B (Angles opposite to equal sides are also equal)
In ΔABC,
∠A + ∠B + ∠C = 180º (Angle sum property of a triangle)
⇒ 90º + ∠B + ∠C = 180º
⇒ 90º + ∠B + ∠B = 180º
⇒ 2 ∠B = 90º
⇒ ∠B = 45º
∴ ∠B = ∠C = 45º
Show that the angles of an equilateral triangle are 60º each.
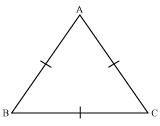
Let us consider that ABC is an equilateral triangle.
Therefore, AB = BC = AC
AB = AC
⇒ ∠C = ∠B (Angles opposite to equal sides of a triangle are equal)
Also,
AC = BC
⇒ ∠B = ∠A (Angles opposite to equal sides of a triangle are equal)
Therefore, we obtain
∠A = ∠B = ∠C
In ΔABC,
∠A + ∠B + ∠C = 180°
⇒ ∠A + ∠A + ∠A = 180°
⇒ 3∠A = 180°
⇒ ∠A = 60°
⇒ ∠A = ∠B = ∠C = 60°
Hence, in an equilateral triangle, all interior angles are of measure 60º.
ΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see the given figure). If AD is extended to intersect BC at P, show that
(i) ΔABD ≅ ΔACD
(ii) ΔABP ≅ ΔACP
(iii) AP bisects ∠A as well as ∠D.
(iv) AP is the perpendicular bisector of BC.
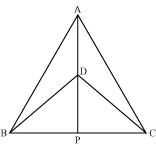
(i) In ΔABD and ΔACD,
AB = AC (Given)
BD = CD (Given)
AD = AD (Common)
∴ ΔABD ≅ ΔACD (By SSS congruence rule)
⇒ ∠BAD = ∠CAD (By CPCT)
⇒ ∠BAP = ∠CAP …. (1)
(ii) In ΔABP and ΔACP,
AB = AC (Given)
∠BAP = ∠CAP [From equation (1)]
AP = AP (Common)
∴ ΔABP ≅ ΔACP (By SAS congruence rule)
⇒ BP = CP (By CPCT) … (2)
(iii) From equation (1),
∠BAP = ∠CAP
Hence, AP bisects ∠A.
In ΔBDP and ΔCDP,
BD = CD (Given)
DP = DP (Common)
BP = CP [From equation (2)]
∴ ΔBDP ≅ ΔCDP (By S.S.S. Congruence rule)
⇒ ∠BDP = ∠CDP (By CPCT) … (3)
Hence, AP bisects ∠D.
(iv) ΔBDP ≅ ΔCDP
∴ ∠BPD = ∠CPD (By CPCT) …. (4)
∠BPD + ∠CPD = 180 (Linear pair angles)
∠BPD + ∠BPD = 180
2∠BPD = 180 [From equation (4)]
∠BPD = 90 … (5)
From equations (2) and (5), it can be said that AP is the perpendicular bisector of BC.
AD is an altitude of an isosceles triangles ABC in which AB = AC. Show that
(i) AD bisects BC (ii) AD bisects ∠A.
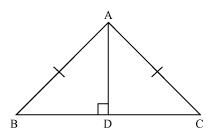
(i) In ΔBAD and ΔCAD,
∠ADB = ∠ADC (Each 90º as AD is an altitude)
AB = AC (Given)
AD = AD (Common)
∴ΔBAD ≅ ΔCAD (By RHS Congruence rule)
⇒ BD = CD (By CPCT)
Hence, AD bisects BC.
(ii) Also, by CPCT,
∠BAD = ∠CAD
Hence, AD bisects ∠A.
Sponsor Area
Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of ΔPQR (see the given figure). Show that:
(i) ΔABM ≅ ΔPQN
(ii) ΔABC ≅ ΔPQR
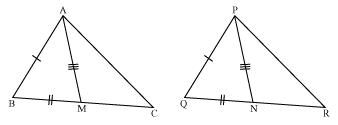
(i) In ΔABC, AM is the median to BC.
∴ BM = BC
In ΔPQR, PN is the median to QR.
∴ QN = QR
However, BC = QR
∴ BC = QR
⇒ BM = QN … (1)
In ΔABM and ΔPQN,
AB = PQ (Given)
BM = QN [From equation (1)]
AM = PN (Given)
∴ ΔABM ≅ ΔPQN (SSS congruence rule)
∠ABM = ∠PQN (By CPCT)
∠ABC = ∠PQR … (2)
(ii) In ΔABC and ΔPQR,
AB = PQ (Given)
∠ABC = ∠PQR [From equation (2)]
BC = QR (Given)
⇒ ΔABC ≅ ΔPQR (By SAS congruence rule)
BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
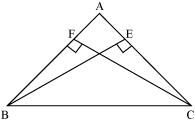
In ΔBEC and ΔCFB,
∠BEC = ∠CFB (Each 90°)
BC = CB (Common)
BE = CF (Given)
∴ ΔBEC ≅ ΔCFB (By RHS congruency)
⇒ ∠BCE = ∠CBF (By CPCT)
∴ AB = AC (Sides opposite to equal angles of a triangle are equal)
Hence, ΔABC is isosceles.
ABC is an isosceles triangle with AB = AC. Drawn AP ⊥ BC to show that ∠B = ∠C.
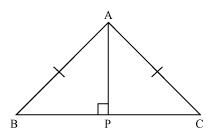
In ΔAPB and ΔAPC,
∠APB = ∠APC (Each 90º)
AB =AC (Given)
AP = AP (Common)
∴ ΔAPB ≅ ΔAPC (Using RHS congruence rule)
⇒ ∠B = ∠C (By using CPCT)
Show that in a right angled triangle, the hypotenuse is the longest side.

Let us consider a right-angled triangle ABC, right-angled at B.
In ΔABC,
∠A + ∠B + ∠C = 180° (Angle sum property of a triangle)
∠A + 90º + ∠C = 180°
∠A + ∠C = 90°
Hence, the other two angles have to be acute (i.e., less than 90º).
∴ ∠B is the largest angle in ΔABC.
⇒ ∠B > ∠A and ∠B > ∠C
⇒ AC > BC and AC > AB
[In any triangle, the side opposite to the larger (greater) angle is longer.]
Therefore, AC is the largest side in ΔABC.
However, AC is the hypotenuse of ΔABC. Therefore, hypotenuse is the longest side in a right-angled triangle.
In the given figure sides AB and AC of ΔABC are extended to points P and Q respectively. Also, ∠PBC < ∠QCB. Show that AC > AB.
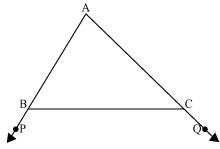
In the given figure,
∠ABC + ∠PBC = 180° (Linear pair)
⇒ ∠ABC = 180° − ∠PBC … (1)
Also,
∠ACB + ∠QCB = 180°
∠ACB = 180° − ∠QCB … (2)
As ∠PBC < ∠QCB,
⇒ 180º − ∠PBC > 180º − ∠QCB
⇒ ∠ABC > ∠ACB [From equations (1) and (2)]
⇒ AC > AB (Side opposite to the larger angle is larger.)
AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see the given figure). Show that ∠A > ∠C and ∠B > ∠D.
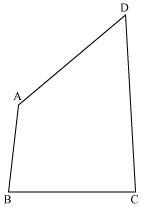
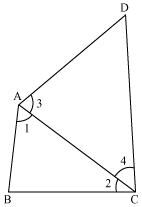
Let us join AC.
In ΔABC,
AB < BC (AB is the smallest side of quadrilateral ABCD)
∴ ∠2 < ∠1 (Angle opposite to the smaller side is smaller) … (1)
In ΔADC,
AD < CD (CD is the largest side of quadrilateral ABCD)
∴ ∠4 < ∠3 (Angle opposite to the smaller side is smaller) … (2)
On adding equations (1) and (2), we obtain
∠2 + ∠4 < ∠1 + ∠3
⇒ ∠C < ∠A
⇒ ∠A > ∠C
Let us join BD.
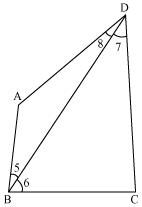
In ΔABD,
AB < AD (AB is the smallest side of quadrilateral ABCD)
∴ ∠8 < ∠5 (Angle opposite to the smaller side is smaller) … (3)
In ΔBDC,
BC < CD (CD is the largest side of quadrilateral ABCD)
∴ ∠7 < ∠6 (Angle opposite to the smaller side is smaller) … (4)
On adding equations (3) and (4), we obtain
∠8 + ∠7 < ∠5 + ∠6
⇒ ∠D < ∠B
⇒ ∠B > ∠D
In the given figure, PR > PQ and PS bisects ∠QPR. Prove that ∠PSR >∠PSQ.
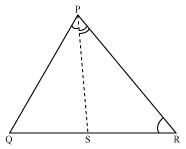
As PR > PQ,
∴ ∠PQR > ∠PRQ (Angle opposite to larger side is larger) … (1)
PS is the bisector of ∠QPR.
∴∠QPS = ∠RPS … (2)
∠PSR is the exterior angle of ΔPQS.
∴ ∠PSR = ∠PQR + ∠QPS … (3)
∠PSQ is the exterior angle of ΔPRS.
∴ ∠PSQ = ∠PRQ + ∠RPS … (4)
Adding equations (1) and (2), we obtain
∠PQR + ∠QPS > ∠PRQ + ∠RPS
⇒ ∠PSR > ∠PSQ [Using the values of equations (3) and (4)]
Show that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest.
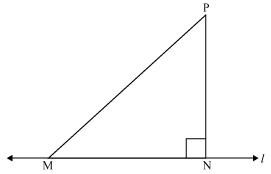
Let us take a line l and from point P (i.e., not on line l), draw two line segments PN and PM. Let PN be perpendicular to line l and PM is drawn at some other angle.
In ΔPNM,
∠N = 90º
∠P + ∠N + ∠M = 180º (Angle sum property of a triangle)
∠P + ∠M = 90º
Clearly, ∠M is an acute angle.
∴ ∠M < ∠N
⇒ PN < PM (Side opposite to the smaller angle is smaller)
Similarly, by drawing different line segments from P to l, it can be proved that PN is smaller in comparison to them.
Therefore, it can be observed that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest.
ABC is a triangle. Locate a point in the interior of ΔABC which is equidistant from all the vertices of ΔABC.
Circumcentre of a triangle is always equidistant from all the vertices of that triangle. Circumcentre is the point where perpendicular bisectors of all the sides of the triangle meet together.
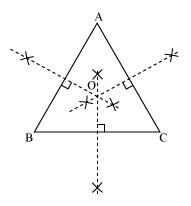
In ΔABC, we can find the circumcentre by drawing the perpendicular bisectors of sides AB, BC, and CA of this triangle. O is the point where these bisectors are meeting together. Therefore, O is the point which is equidistant from all the vertices of ΔABC.
In a triangle locate a point in its interior which is equidistant from all the sides of the triangle.
The point which is equidistant from all the sides of a triangle is called the incentre of the triangle. Incentre of a triangle is the intersection point of the angle bisectors of the interior angles of that triangle.
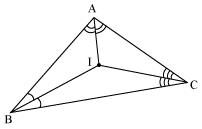
Here, in ΔABC, we can find the incentre of this triangle by drawing the angle bisectors of the interior angles of this triangle. I is the point where these angle bisectors are intersecting each other. Therefore, I is the point equidistant from all the sides of ΔABC.
In a huge park people are concentrated at three points (see the given figure)

A: where there are different slides and swings for children,
B: near which a man-made lake is situated,
C: which is near to a large parking and exit.
Where should an ice-cream parlour be set up so that maximum number of persons can approach it?
(Hint: The parlor should be equidistant from A, B and C)
Maximum number of persons can approach the ice-cream parlour if it is equidistant from A, B and C. Now, A, B and C form a triangle. In a triangle, the circumcentre is the only point that is equidistant from its vertices. So, the ice-cream parlour should be set up at the circumcentre O of ΔABC.
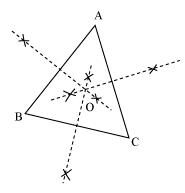
In this situation, maximum number of persons can approach it. We can find circumcentre O of this triangle by drawing perpendicular bisectors of the sides of this triangle.
Complete the hexagonal and star shaped rangolies (see the given figures) by filling them with as many equilateral triangles of side 1 cm as you can. Count the number of triangles in each case. Which has more triangles?
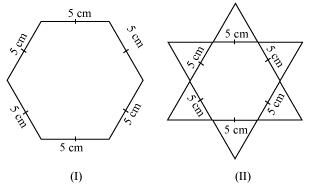
It can be observed that hexagonal-shaped rangoli has 6 equilateral triangles in it.
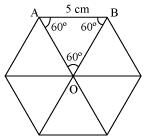
Area of ΔOAB
Area of hexagonal-shaped rangoli
Area of equilateral triangle having its side as 1 cm
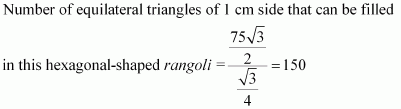
Star-shaped rangoli has 12 equilateral triangles of side 5 cm in it.
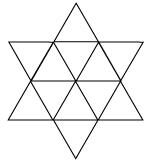
Area of star-shaped rangoli =
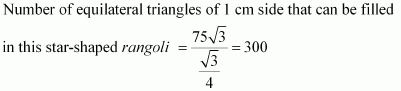
Therefore, star-shaped rangoli has more equilateral triangles in it.
Mock Test Series
Sponsor Area
Sponsor Area