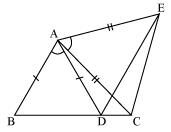
AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (See the given figure). Show that
(i) ΔDAP ≅ ΔEBP
(ii) AD = BE
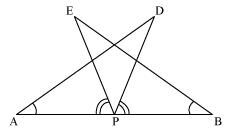
It is given that ∠EPA = ∠DPB
⇒ ∠EPA + ∠DPE = ∠DPB + ∠DPE
⇒ ∠DPA = ∠EPB
In ΔDAP and ΔEBP,
∠DAP = ∠EBP (Given)
AP = BP (P is mid-point of AB)
∠DPA = ∠EPB (From above)
∴ ΔDAP ≅ ΔEBP (ASA congruence rule)
∴ AD = BE (By CPCT)