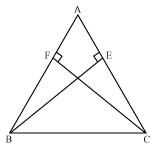
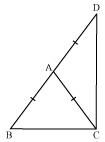
ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see the given figure). Show that these altitudes are equal.
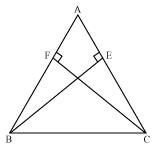
In ΔAEB and ΔAFC,
∠AEB and ∠AFC (Each 90º)
∠A = ∠A (Common angle)
AB = AC (Given)
∴ ΔAEB ≅ ΔAFC (By AAS congruence rule)
⇒ BE = CF (By CPCT)