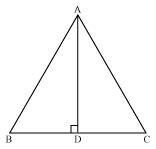
Show that the angles of an equilateral triangle are 60º each.
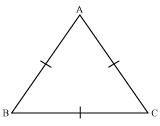
Let us consider that ABC is an equilateral triangle.
Therefore, AB = BC = AC
AB = AC
⇒ ∠C = ∠B (Angles opposite to equal sides of a triangle are equal)
Also,
AC = BC
⇒ ∠B = ∠A (Angles opposite to equal sides of a triangle are equal)
Therefore, we obtain
∠A = ∠B = ∠C
In ΔABC,
∠A + ∠B + ∠C = 180°
⇒ ∠A + ∠A + ∠A = 180°
⇒ 3∠A = 180°
⇒ ∠A = 60°
⇒ ∠A = ∠B = ∠C = 60°
Hence, in an equilateral triangle, all interior angles are of measure 60º.