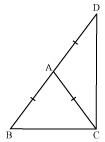
ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA (See the given figure). Prove that
(i) ΔABD ≅ ΔBAC
(ii) BD = AC
(iii) ∠ABD = ∠BAC.
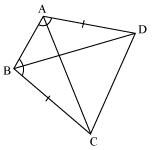
In ΔABD and ΔBAC,
AD = BC (Given)
∠DAB = ∠CBA (Given)
AB = BA (Common)
∴ ΔABD ≅ ΔBAC (By SAS congruence rule)
∴ BD = AC (By CPCT)
And, ∠ABD = ∠BAC (By CPCT)
In ΔABC, AD is the perpendicular bisector of BC (see the given figure). Show that ΔABC is an isosceles triangle in which AB = AC.
ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see the given figure). Show that these altitudes are equal.
ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see the given figure). Show that
(i) ΔABE ≅ ΔACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.
ΔABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see the given figure). Show that ∠BCD is a right angle.
ABC is a right angled triangle in which ∠A = 90º and AB = AC. Find ∠B and ∠C.
Show that the angles of an equilateral triangle are 60º each.
AD is an altitude of an isosceles triangles ABC in which AB = AC. Show that
(i) AD bisects BC (ii) AD bisects ∠A.
Mock Test Series
