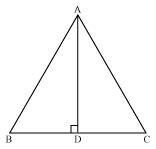
Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of ΔPQR (see the given figure). Show that:
(i) ΔABM ≅ ΔPQN
(ii) ΔABC ≅ ΔPQR
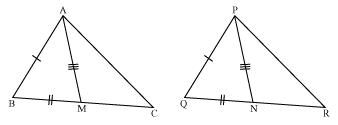
(i) In ΔABC, AM is the median to BC.
∴ BM = BC
In ΔPQR, PN is the median to QR.
∴ QN = QR
However, BC = QR
∴ BC = QR
⇒ BM = QN … (1)
In ΔABM and ΔPQN,
AB = PQ (Given)
BM = QN [From equation (1)]
AM = PN (Given)
∴ ΔABM ≅ ΔPQN (SSS congruence rule)
∠ABM = ∠PQN (By CPCT)
∠ABC = ∠PQR … (2)
(ii) In ΔABC and ΔPQR,
AB = PQ (Given)
∠ABC = ∠PQR [From equation (2)]
BC = QR (Given)
⇒ ΔABC ≅ ΔPQR (By SAS congruence rule)