Mathematics Chapter 16 Proofs In Mathematics
Sponsor Area
NCERT Solution For Class 9 About 2.html
Give five examples of data that you can collect from your day-to-day life.
(i) Number of students in our class,
(ii) Number of fans in our school.
(iii) Electricity bills of our house for last two years.
(iv) Election results obtained from television or newspaper.
(v) Literacy rate figures obtained from
Classify the data in Q. 1 above as primary or secondary data.
The blood groups of 30 students of Class VIII are recorded as follows:
A,B,O,O,AB,O,A O,B,A,O,B, A,O,O,
A,AB,O,A,A,O,O,AB,B,A,O,B,A,B.O.
Represent this data in the form of a frequency distribution table. Which is the most common and which is the rarest, blood group among these students.

O is the most common and AB is the rarest blood group among these students.
The distance (in km) of 40 engineers from their residence to their place of work were found as follows:
5 3 10 20 25 11 13 7 12 31
19 10 12 17 18 11 32 17 16 2
7 9 7 8 3 5 12 15 18 3
12 14 2 9 6 15 15 7 6 12
Construct a grouped frequency distribution table with class size 5 for the data given above, taking the first interval as 0–5 (5 not included). What main features do you observe from this tabular representation ?
(i)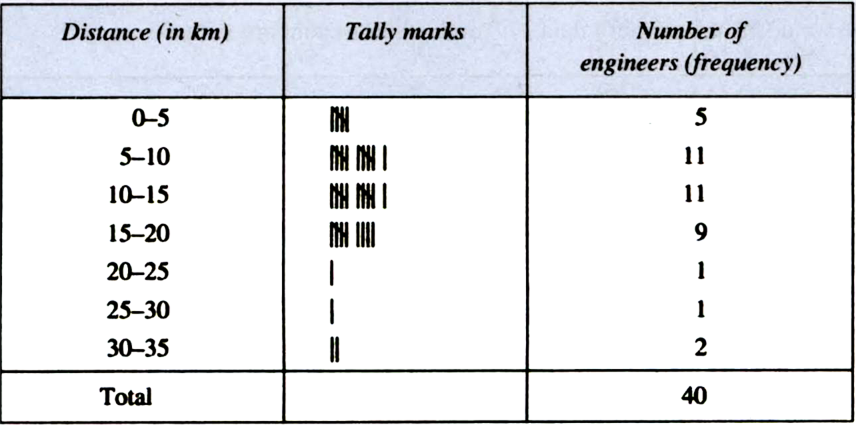
We observe the following main features from this tabular representation:
(i) The distances (in km) from their residence to their work place of the maximum number of engineers are in the third interval, i.e., 10–15.
(ii) The distances (in km) from their residence to their work place of the minimum number of engineers are in the intervals 20–25 and 25–30 each.
(iii) The frequencies of the intervals 20–25 and 25–30 are the same. (Each = 1)
The relative humidity (in %) of a certain city for a month of 30 days is as follows:
98.1 98.6 99.2 90.3 86.5 95.3 92.9 96.3 94.2 95.1
89.2 92.3 97.1 93.5 92.7 95.1 97.2 93.3 95.2 97.3
96.2 92.1 84.9 90.2 95.7 98.3 97.3 96.1 92.1 89
(i) Construct a grouped frequency distribution table with classes 84-86, 86-88, etc.
(ii) Which month or season do you think this data is about?
(iii) What is the range of this data?
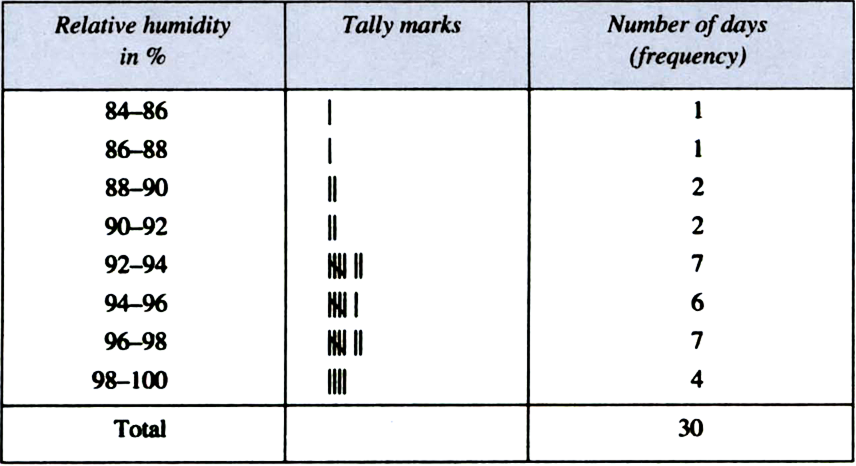
(ii) This data appears to be taken in the rainy reason as the relative humidity is high.
(iii) Range = Highest value – Lowest value = 99.2 – 84.9= 14.3 (in %).
The heights of 50 students, measured to the nearest centimetres, have been found to be as follows:
161 150 154 165 168 161 154 162 150 151
162 164 171 165 158 154 156 172 160 170
153 159 161 170 162 165 166 168 165 164
154 152 153 156 158 162 160 161 173 166
161 159 162 167 168 159 158 153 154 159
(i) Represent the data given above by a grouped frequency distribution table, taking the class intervals as 160–165, 165–170, etc.
(ii) What can you conclude about their heights from the table?
(i)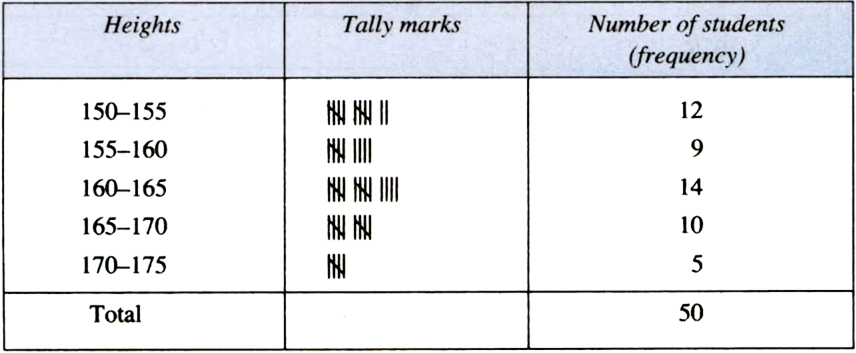
(ii) The heights of maximum number of students are in the group 160–165 and the heights of minimum number of students are in the group 170–175.
(iii) More than 50% of students are shorter than 165 cm.
A study was conducted to find out the concentration of sulphur dioxide in the air in parts per million (ppm) of a certain city. The data obtained for 30 days is as follows :
0.03 0.08 0.08 0.09 0.04 0.17
0.16 0.05 0.02 0.06 0.18 0.20
0.11 0.08 0.12 0.13 0.22 0.07
0.08 0.01 0.10 0.06 0.09 0.18
0.11 0.07 0.05 0.07 0.01 0.04
(i) Make a grouped frequency distribution table for this data with class intervals as 0.00–0.04, 0.04–0.08, and so on.
(ii) For how many days, was the concentration of sulphur dioxide more than 0.11 parts per million?
(i)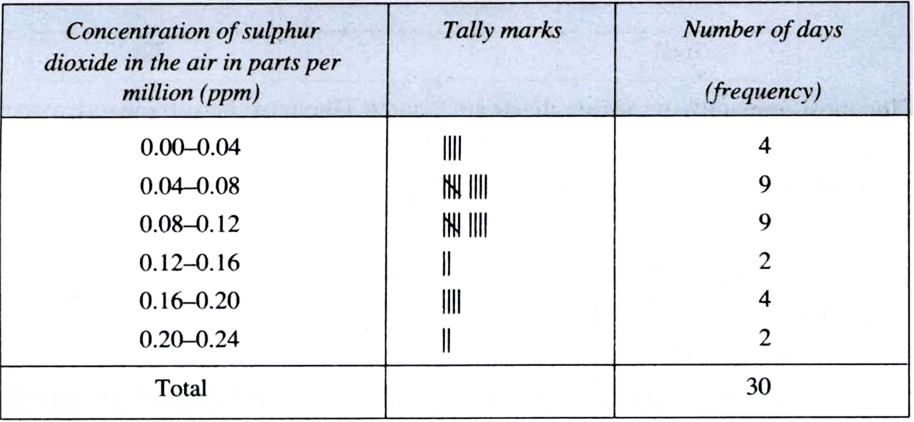
(ii) The concentration of sulphur dioxide was more than 0.11 parts per million for 2 + 4 + 2 = 8 days.
The value of π 50 decimal places is given below:
3.14159265358979323846264338327950288419716939937510
(i) Make a frequency distribution of the digits from 0 to 9 after the decimal point.
(ii) What are the most and the least frequently occurring digits?
(i)
(ii) The most frequently occurring digits are 3 and 9. The most least frequently occurring digit is 0.
Thirty children were asked about the number of hours they watched TV programmes in the previous week. The results were found as follows:
1 6 2 3 5 1 2 5 8 4 8
10 3 4 12 2 8 15 1 17 6
3 2 8 5 9 6 8 7 14 12
(i) Make a grouped frequency distribution table for this data, taking class width 5 and one of the class intervals as 5–0.
(ii) How many children watched television for 15 or more hours a week?
(i)
(ii) 2 children watched television for 15 or more hours a week.
The class marks of a frequency distribution are 104, 114, 124, 134, 144, 154, 164. Find the class size and class intervals.
Class size = 114 – 104 = 10![]()
The class intervals are
104 – 5 — 104 + 5, i.e., 99 – 109;
114 – 5 — 114 + 5, i.e., 109 –119;
124 – 5 — 124 + 5, i.e., 119 – 129;
134 – 5 — 134 + 5, i.e., 129 – 139;
144 – 5 —144 + 5, i.e., 139 – 149;
154 – 5 — 154 + 5, i.e„ 149 – 159;
164 – 5 — 164 + 5, i.e., 159 – 9.
The number of books in different shelves of a library are as follows: 25, 27, 32, 24, 28,
34, 20, 25, 28, 30,
20, 35, 25, 27, 31,
37, 22, 24, 27, 28,
27, 20, 36, 21, 20,
29, 30, 29, 36, 30
Prepare a frequency distribution table with class size 4 for the data given above taking the first interval as 18–22. (22 not included).

The blood group of 20 students are recorded as follows:
A, B, O, O, AB, O, A, O, B, A, O, AB, O, A, A, O. B, A, B, O
Represent this data in the form of a frequency distribution table. Which is the rarest blood group?

The rarest blood group is AB as the frequency of the students with this blood group is the least.
The distance in km of 32 engineers from their residence to their place of work were found as follows:
4, 6, 10,12, 8, 13, 12, 9, 11, 16, 10, 18, 15, 3, 8, 4,
10, 8, 7, 9, 5, 15, 18, 3, 11, 15, 2, 10, 14, 7, 6, 12
Construct a grouped frequency distribution table with class-size for the data given above taking the first interval as 0–5.
A part of the frequency table is given below:
|
Class marks of weights (in kg) |
No. of students |
|
33 |
9 |
|
38 |
5 |
|
43 |
14 |
Rewrite the table with class limits.
|
Class intervals |
No. of students |
|
31.5–35.5 |
9 |
|
35.5–40.5 |
5 |
|
40.5-45.5 |
14 |
Sponsor Area
The marks obtained out of 75 by 30 students of a class in an examination are given below:
42, 21, 50, 37,42, 37, 38, 42, 49, 52, 38, 53, 57, 47, 29, 59, 61, 33, 17, 17, 39, 44, 42, 39, 14, 7, 27, 19, 54, 51
Prepare a frequency distribution table in which the size of class intervals is the same and one class interval is 0–10.
|
Class |
Frequency |
|
0–10 |
1 |
|
10–20 |
4 |
|
20–30 |
3 |
|
30–40 |
7 |
|
40–50 |
7 |
|
50–60 |
7 |
|
60–70 |
1 |
|
Total |
30 |
The weights (in grams) of 30 apples picked at random from a basket of oranges are given below:
45, 55, 30, 110,75, 100, 40, 60, 65, 40, 100, 75, 70, 60, 70, 70, 60, 95, 85, 80, 35, 45,40, 50, 60, 65, 55, 45, 30, 90
Prepare a frequency distribution table in which the size of class intervals is the same and one class interval is 30–40.
|
Weight of oranges (in grams) |
Frequency |
|
30–40 |
3 |
|
40–50 |
6 |
|
50–60 |
3 |
|
60–70 |
6 |
|
70–80 |
5 |
|
80–90 |
2 |
|
90–100 |
2 |
|
100–110 |
2 |
|
110–120 |
1 |
|
Total |
30 |
In a specific year, the distribution of the ages (in years) of primary teachers of a district is given:
|
Age (in years) |
Number of teachers |
|
15–20 |
10 |
|
20–25 |
30 |
|
25–30 |
50 |
|
30–35 |
50 |
|
35–40 |
30 |
|
40–45 |
6 |
|
45–50 |
4 |
(i) What is the lower limit of the first class interval?
(ii) What are the limits of the fourth class interval?
(iii) What is the class mark of the class 45–50?
The marks obtained by 40 students of class IX in an examination are given below:
12, 8, 18, 8, 6, 16, 12, 5,
23, 2, 10, 20, 12, 9, 7, 6,
5, 3 , 5, 13, 21, 13,15, 20,
24, 1, 7, 16, 21, 13, 23, 18,
7, 3, 18, 17, 16, 16, 23, 12
Represent the data in the form of a frequency distribution using 15–20 (20 not included) as one of the class intervals.
|
0–5 |
4 |
|
5–10 |
11 |
|
10–15 |
8 |
|
15–20 |
9 |
|
20–25 |
8 |
Prepare a freauency table from the data below:
|
Marks obtained |
No. of students |
|
More than or equal to 0 |
50 |
|
More than or equal to 20 |
48 |
|
More than or equal to 40 |
41 |
|
More than or equal to 60 |
30 |
|
More than or equal to 80 |
12 |
|
0–20 |
2 |
|
20–40 |
7 |
|
40–60 |
11 |
|
60–80 |
18 |
|
80 & above |
12 |
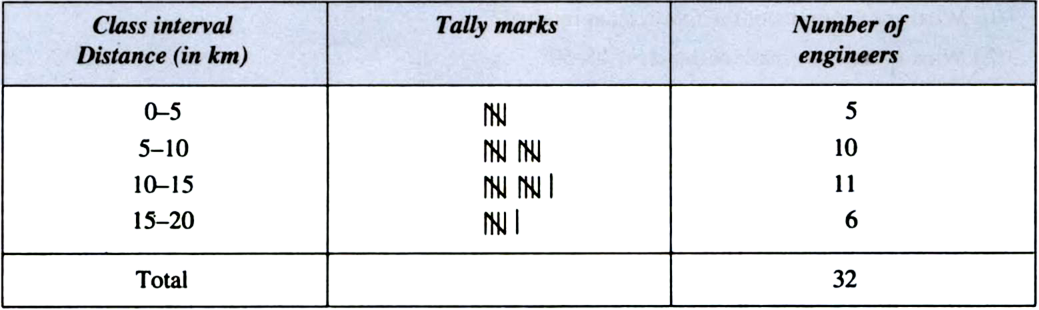
A survey conducted by an organisation for the cause of illness and death among the women between the ages 15—44 (in years) worldwide, found the following figures (in %):
|
S.No. |
Causes |
Female fatality rate (%) |
|
1. |
Reproductive health conditions |
31.8 |
|
2. |
Neuropsychiatric conditions |
25.4 |
|
3. |
Injuries |
12.4 |
|
4. |
Cardiovascular conditions |
4.3 |
|
5. |
Respiratory conditions |
4.1 |
|
6. |
Other causes |
22.0 |
(i) Represent the information given above graphically.
(ii) Which condition is the major cause of women–s ill health and death worldwide?
(iii) Try to find out, with the help of your teacher, any two factors which play a major role in the cause in (ii) above being the major cause.
(i)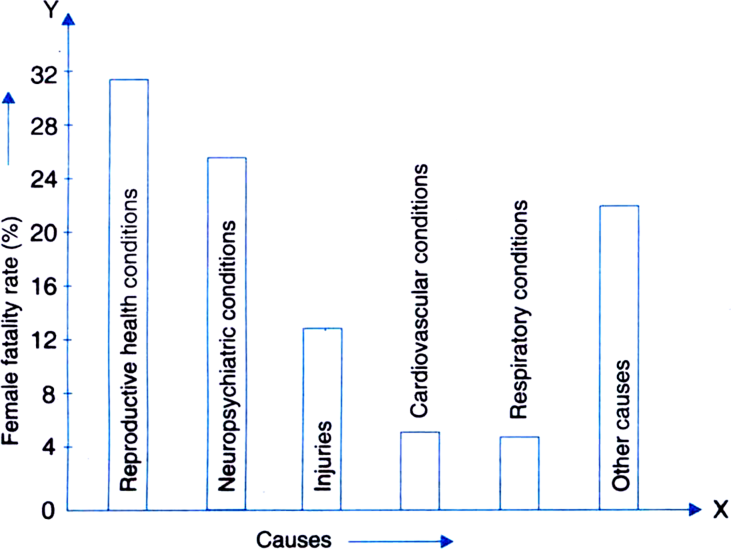
(ii) Reproductive health conditions is the major cause of women’s ill health and death worldwide.
(iii) Lack of proper diet, lack of advised exercises.
The following data on the number of girls (to the nearest ten) per thousand boys in different sections of the Indian society is given below:
|
Section |
Number of girls per thousand boys |
|
Scheduled caste (SC) |
940 |
|
Scheduled tribe (ST) |
970 |
|
Non SC/ST |
920 |
|
Backward districts |
950 |
|
Non-backward districts |
920 |
|
Rural |
930 |
|
Urban |
910 |
(i) Represent the information above by a bar graph.
(ii) In the classroom discuss what conclusion can be arrived at from the graph.
(i)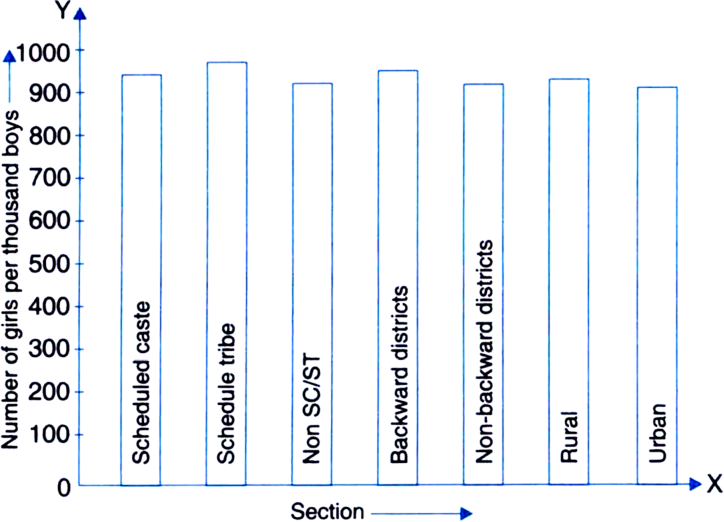
(ii) The two conclusions we can arrive at from the graph are as follows:
(a) The numbers of girls to the nearest ten per thousand boys is maximum in Scheduled Tribe section of the society and minimum in Urban section of the society.
(b) The number of girls to the nearest ten per thousand boys is the same for ‘Non SC/ST’ and ‘Non-backward Districts’ sections of the society.
Given below are the seats won by different political parties in the polling outcome of a state assembly elections:
|
Political party |
A |
B |
C |
D |
E |
F |
|
Seats won |
75 |
55 |
37 |
29 |
10 |
37 |
(i) Draw a bar graph to represent the polling results. [Hint: First make the class intervals continuous.]
(ii) Which political party won the maximum number of seats?
(i)
(ii) Political party A won the maximum number of seats.
The length of 40 leaves of a plant are measured correct to one millimetre, and the obtained data is represented in the following table:
|
Length (in mm) |
Number of leaves |
|
118–126 |
3 |
|
127–135 |
5 |
|
136–144 |
9 |
|
145–153 |
12 |
|
154–162 |
5 |
|
163–171 |
4 |
|
172–180 |
2 |
(i) Draw a histogram to represent the given data.
(ii) Is there any other suitable graphical representation for the same data?
(iii) Is it correct to conclude that the maximum number of leaves are 153 mm long? Why?
(i) Modified continuous Distribution
|
Length (in mm) |
Number of leaves |
|
117.5–126.5 |
3 |
|
126.5–135.5 |
5 |
|
135.5–144.5 |
9 |
|
144.5–153.5 |
12 |
|
153.5–162.5 |
5 |
|
162.5–171.5 |
4 |
|
171.5–180.5 |
2 |
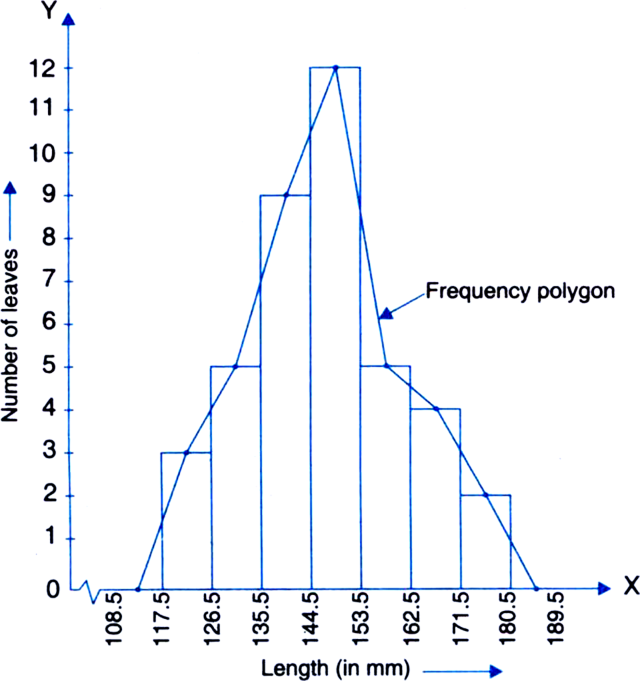
(ii) Frequency Polygon.
(iii) No because the maximum number of leaves have their lengths lying in the interval 145–153.
The following table gives the life times of 400 neon lamps:
|
Life time (in hours) |
Number of lamps |
|
300–400 |
14 |
|
400–500 |
56 |
|
500–600 |
60 |
|
600–700 |
86 |
|
700–800 |
74 |
|
800–900 |
62 |
|
900–1000 |
48 |
(i) Represent the given information with the help of a histogram.
(ii) How many lamps have a life time of more than 700 hours?
(i)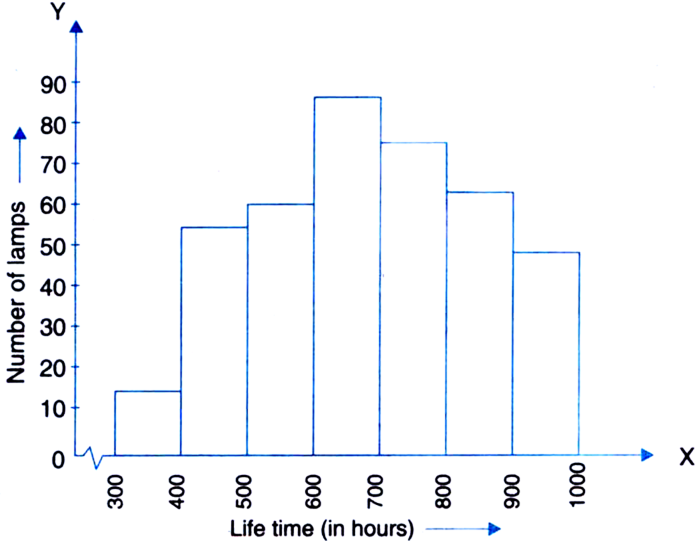
(ii) 74 + 62 + 48 = 184 lamps have a life time of more than 700 hours.
The following table gives the distribution of students of two sections according to the marks obtained by them:
|
Section A |
Section B |
||
|
Marks |
Frequency |
Marks |
Frequency |
|
0–10 |
3 |
0–10 |
5 |
|
10–20 |
9 |
10–20 |
19 |
|
20–30 |
17 |
20–30 |
15 |
|
30–40 |
12 |
30–40 |
10 |
|
40–50 |
9 |
40–50 |
1 |
Represent the marks of the students of both the sections on the same graph by two frequency polygons. From the two polygons compare the performance of the two sections.
Modified Tables
For section A
|
Classes |
Class marks |
Frequency |
|
0–10 |
5 |
3 |
|
10–20 |
15 |
9 |
|
20–30 |
25 |
17 |
|
30–40 |
35 |
12 |
|
40–50 |
45 |
9 |
For section B
|
Classes |
Class marks |
Frequency |
|
0–10 |
5 |
5 |
|
10–20 |
15 |
19 |
|
20–30 |
25 |
15 |
|
30–40 |
35 |
10 |
|
40–50 |
45 |
1 |
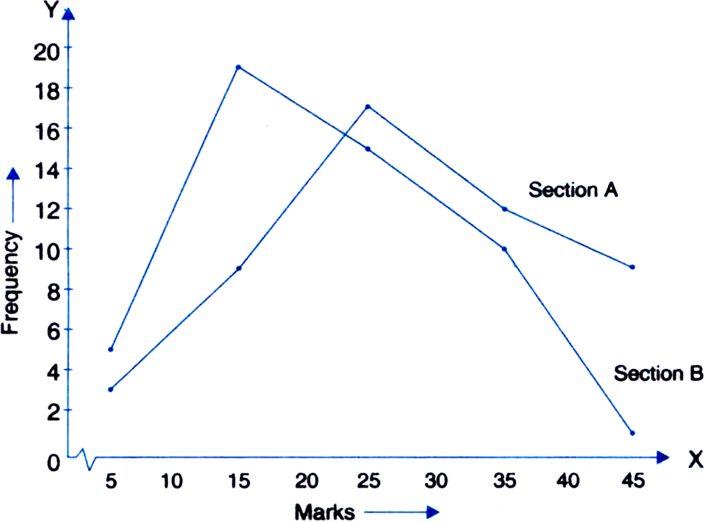
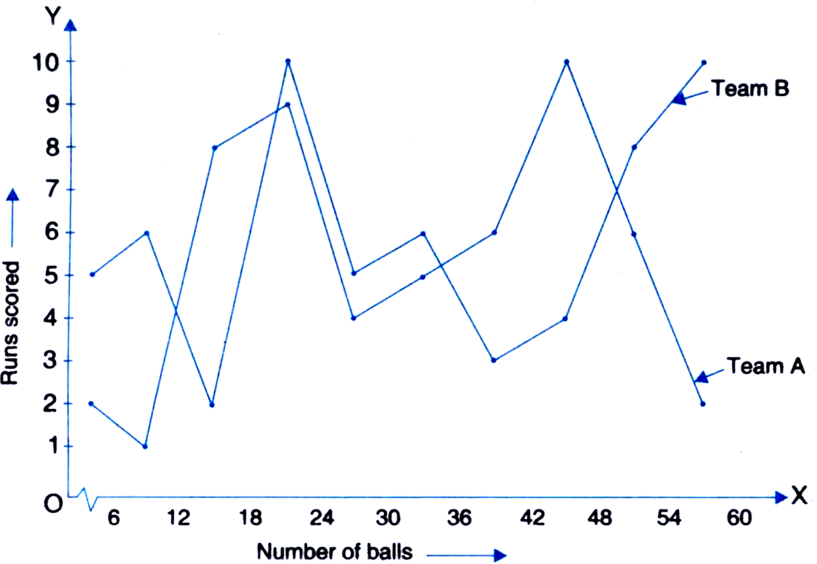
The runs scored by two teams A and B on the first 60 balls in a cricket match are given below:
|
Number of balls |
Team A |
Team B |
|
1–6 |
2 |
5 |
|
7–12 |
1 |
6 |
|
13–18 |
8 |
2 |
|
19–24 |
9 |
10 |
|
25–30 |
4 |
5 |
|
31–36 |
5 |
6 |
|
37–42 |
6 |
3 |
|
43–48 |
10 |
4 |
|
49–54 |
6 |
8 |
|
55–60 |
2 |
10 |
Represent the data of both the teams on the same graph by frequency polygons.
[Hint. First make the class interval continuous.]
Modified Table
|
Number of balls |
Class marks |
Team A |
Team B |
|
0.5–6.5 |
3.5 |
2 |
5 |
|
6.5–12:5 |
9.5 |
1 |
6 |
|
12.5–18.5 |
15.5 |
8 |
2 |
|
18.5–24.5 |
21.5 |
9 |
10 |
|
24.5–30.5 |
27.5 |
4 |
5 |
|
30.5–36.5 |
33.5 |
5 |
6 |
|
36.5–42.5 |
39.5 |
6 |
3 |
|
42.5–48.5 |
45.5 |
10 |
4 |
|
48.5–54.5 |
51.5 |
6 |
8 |
|
54.5–60.5 |
57.5 |
2 |
10 |
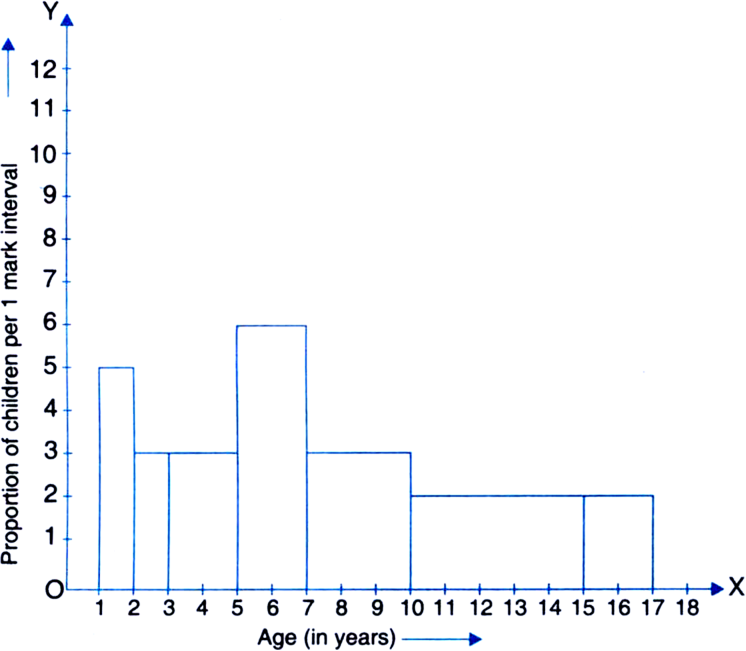
A random survey of the number of children of various age groups playing in a park was found as follows:
|
Age (in years) |
Number of children |
|
1–2 |
5 |
|
2–3 |
3 |
|
3–5 |
6 |
|
5–7 |
12 |
|
7–10 |
9 |
|
10–15 |
10 |
|
15–17 |
4 |
Draw a histogram to represent the data above.


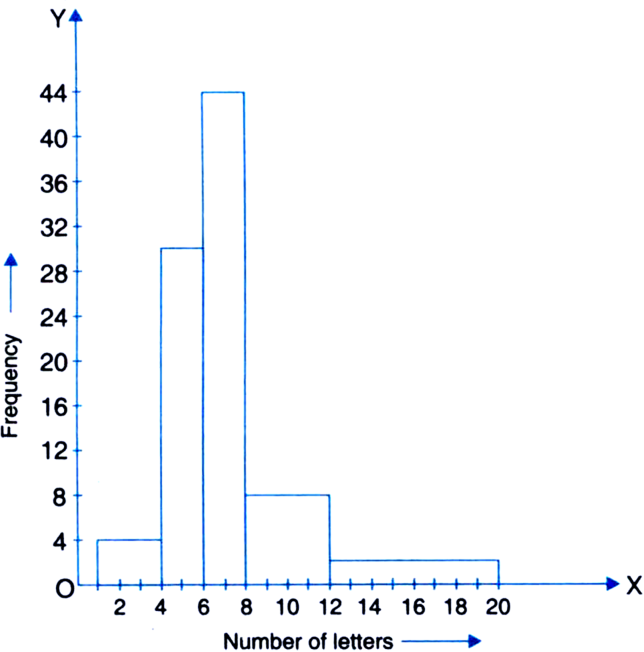
00 surnames were randomly picked up from a local telephone directory and a frequency distribution of the number of letters in the English alphabet in the surnames was found as follows:
|
Number of letters |
Number of surnames |
|
1–4 |
6 |
|
4–6 |
30 |
|
6–8 |
44 |
|
8–12 |
16 |
|
12–20 |
4 |
(i) Draw a histogram to depict the given information.
(ii) Write the class interval in which the maximum number of surnames lie.
(i) Modified Table
[Minimum class-size = 2]
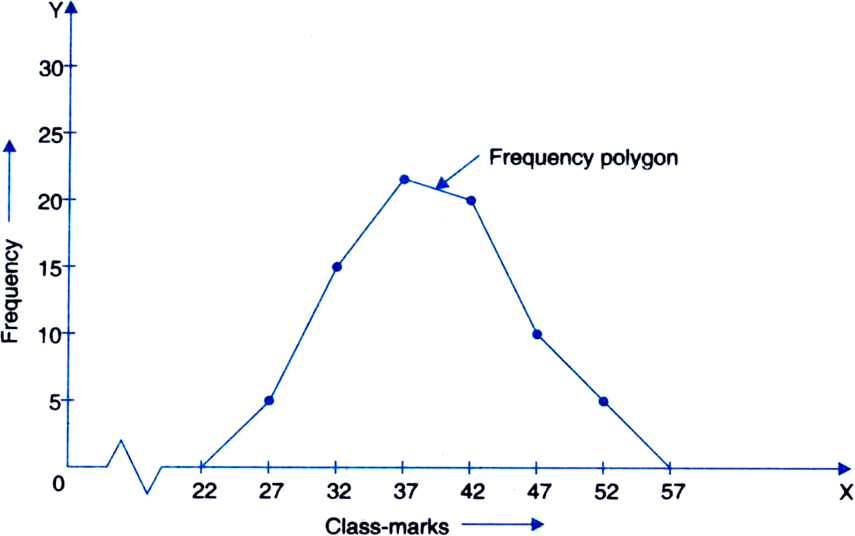
Draw a frequency polygon to represent the following information:
|
Class |
Frequency |
|
25–29 |
5 |
|
30–34 |
15 |
|
35–39 |
23 |
|
40–44 |
20 |
|
45–49 |
10 |
|
50–54 |
7 |
We shall first make the class intervals continuous. Then, the modified table is as follows:
|
Class |
Class-marks |
Frequency |
|
24.5–29.5 |
27 |
5 |
|
29.5–34.5 |
32 |
15 |
|
34.5–39.5 |
37 |
23 |
|
39.5–44.5 |
42 |
20 |
|
44.5–49.5 |
47 |
10 |
|
49.5–54.5 |
52 |
7 |
|
Total |
80 |
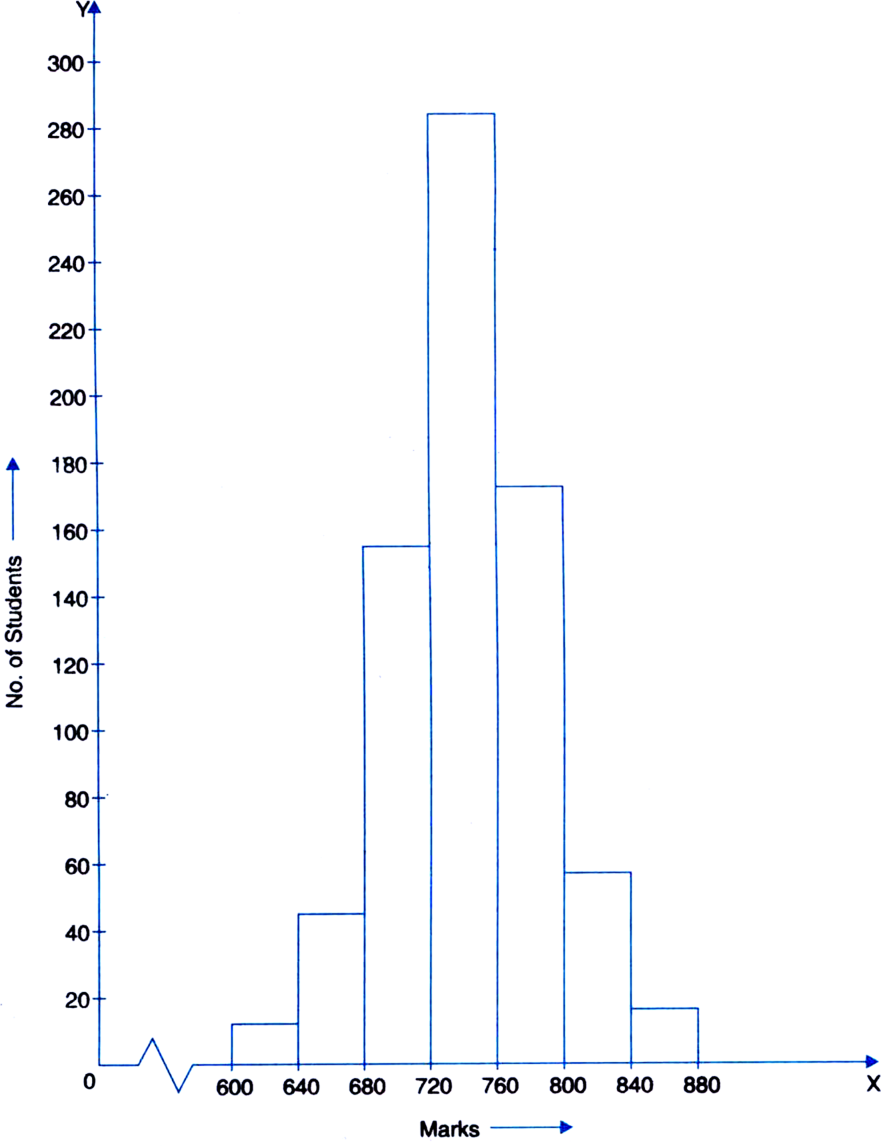
The marks scored by 750 students in examination are given in the form of a frequency distribution table.
|
Marks |
No. of students |
|
600–640 |
16 |
|
640–680 |
45 |
|
680–720 |
156 |
|
720–760 |
284 |
|
760800 |
172 |
|
800–840 |
59 |
|
840–880 |
18 |
Draw a histogram to represent the above data.
Drhistogram and frequency polygon of the following data:
|
Marks |
No. of students |
|
20–30 |
5 |
|
30–40 |
12 |
|
40–50 |
6 |
|
50–60 |
20 |
|
60–70 |
18 |
|
70–80 |
10 |
|
80–90 |
16 |
|
90–100 |
3 |
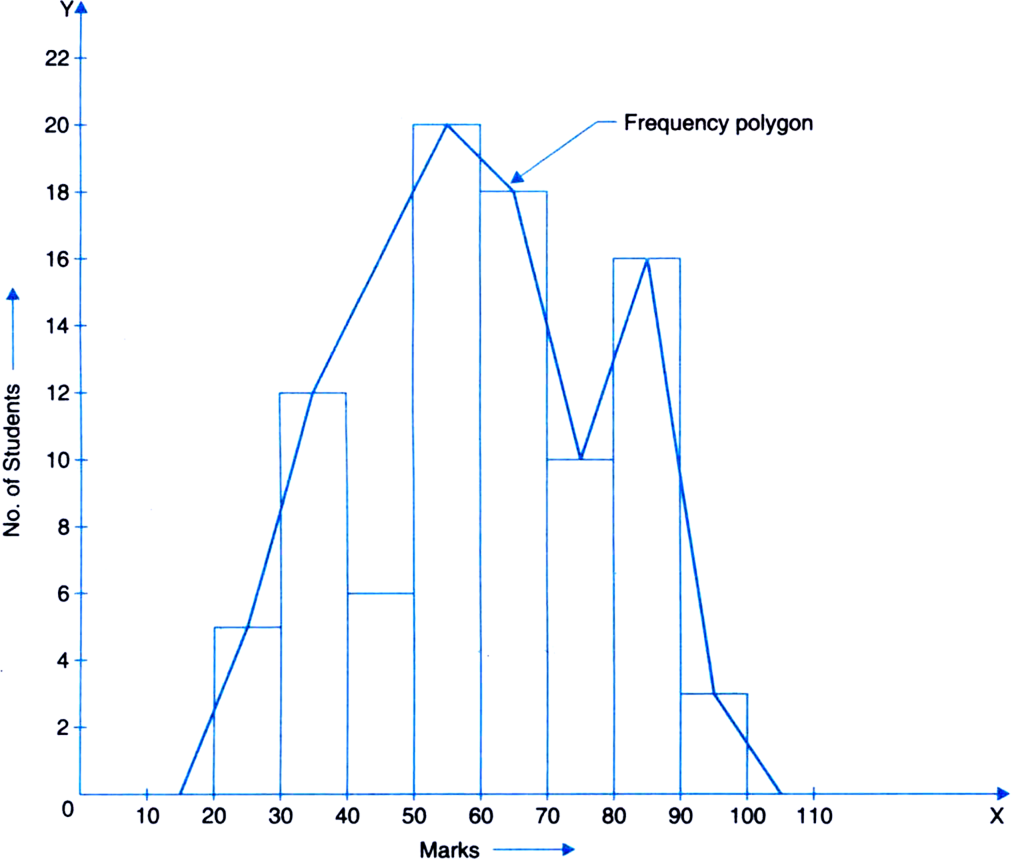
The following table gives the performance of 90 students in a mathematics test of 100 marks.
|
Marks |
Number of students |
|
0–20 |
07 |
|
20–30 |
10 |
|
30–40 |
10 |
|
40–50 |
20 |
|
50–60 |
20 |
|
60–70 |
15 |
|
70–above |
08 |
|
Total |
90 |
Represent the given information with the help of a histogram.
Adjust frequency =
Minimum class size = 10

Sponsor Area
Read the bar graph. Find the percentage of excess expenditure on wheat than pulses and ghee taken together.
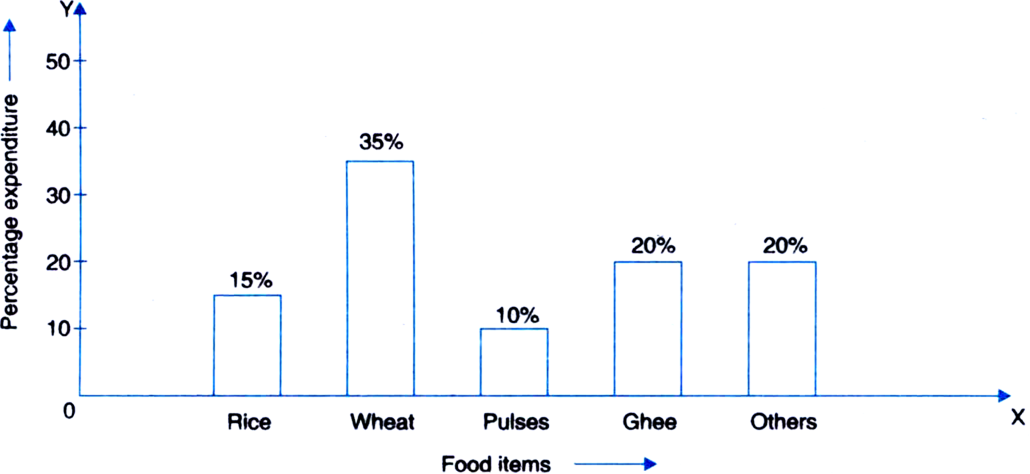
Percentage of excess expenditure on wheat than pulses and ghee taken together
= 35% – (10%+ 20%)
= 5%
For the following data, draw a histogram.
|
Age (in years) |
Number of persons |
|
0–6 |
8 |
|
6–12 |
12 |
|
12–18 |
15 |
|
18–24 |
18 |
|
24–30 |
12 |
|
30–36 |
4 |

Draw a histogram representing the following frequency distribution:
|
Marks |
No. of students |
|
0–10 |
3 |
|
10–20 |
5 |
|
20–30 |
8 |
|
30–40 |
10 |
|
40–50 |
7 |
|
50–60 |
2 |
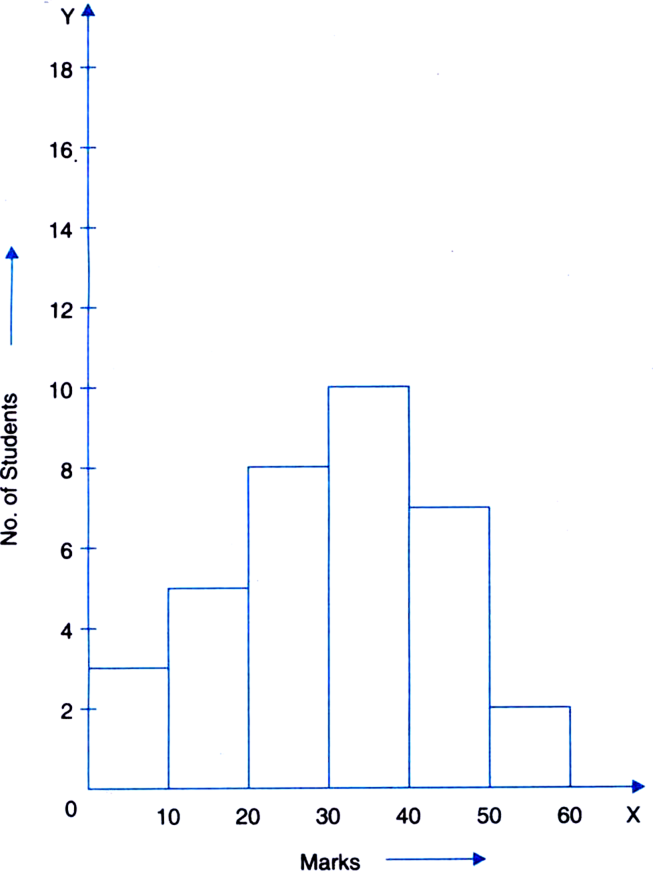
Construct a histogram and frequency polygon for the following data:
|
Monthly school fee र |
No. of schools |
|
600–800 |
5 |
|
800–1000 |
12 |
|
1000–1200 |
14 |
|
1200–1400 |
18 |
|
1400–1600 |
10 |
|
1600–1800 |
9 |
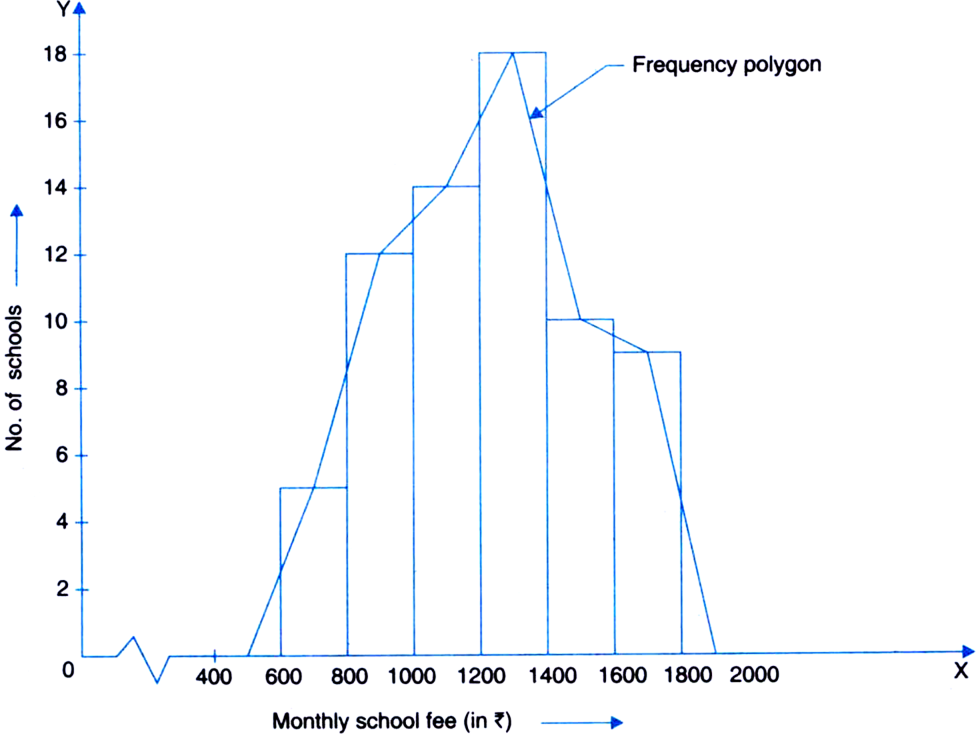
The following table gives the distribution of 60 students according to marks obtained by them
|
Marks |
Frequency |
|
0–10 |
3 |
|
10–20 |
9 |
|
20–30 |
18 |
|
30–40 |
16 |
|
40–50 |
12 |
|
50–60 |
2 |
Draw the frequency polygon for the above data.
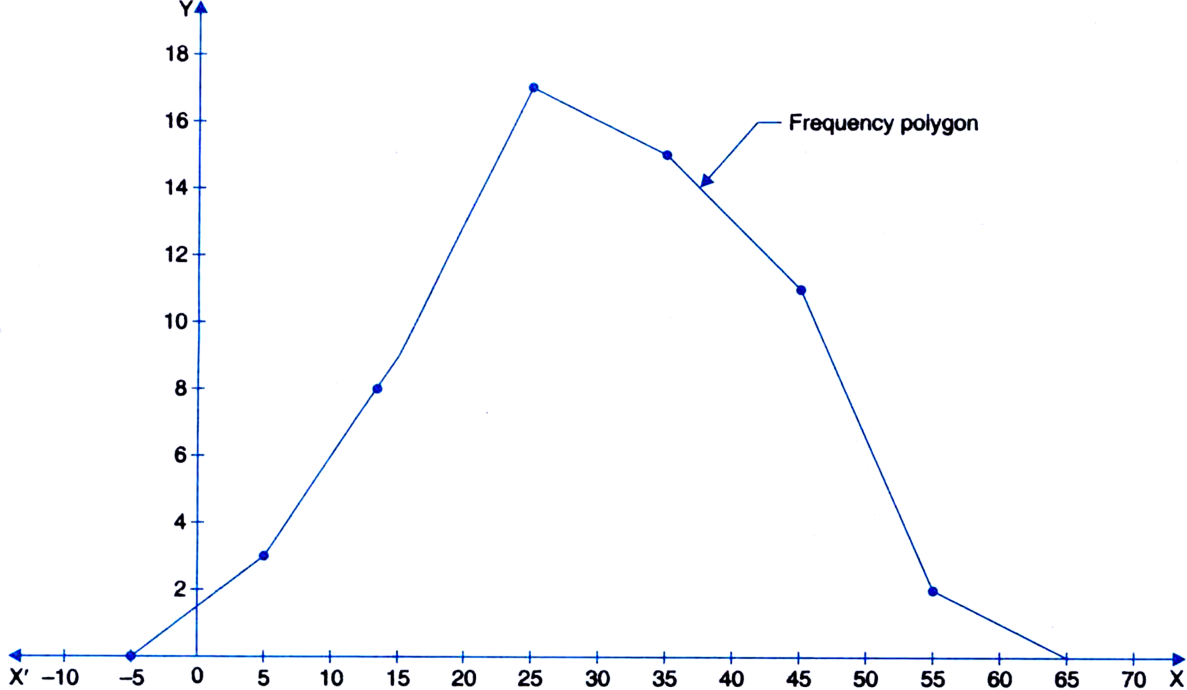
The following table gives the life times of 400 neon lamps:
|
Life time (in hours) |
Number of lamps |
|
300–400 |
14 |
|
400–500 |
56 |
|
500–600 |
60 |
|
600–700 |
86 |
|
700–800 |
74 |
|
800–900 |
62 |
|
900–1000 |
48 |
Represent the above information with the help of a frequency polygon.
|
Life time (in hours) |
Class marks |
Number of lamps (frequency) |
|
300–400 |
350 |
14 |
|
400–500 |
450 |
56 |
|
500–600 |
550 |
60 |
|
600–700 |
650 |
86 |
|
700–800 |
750 |
74 |
|
800–900 |
850 |
62 |
|
900–1000 |
950 |
48 |
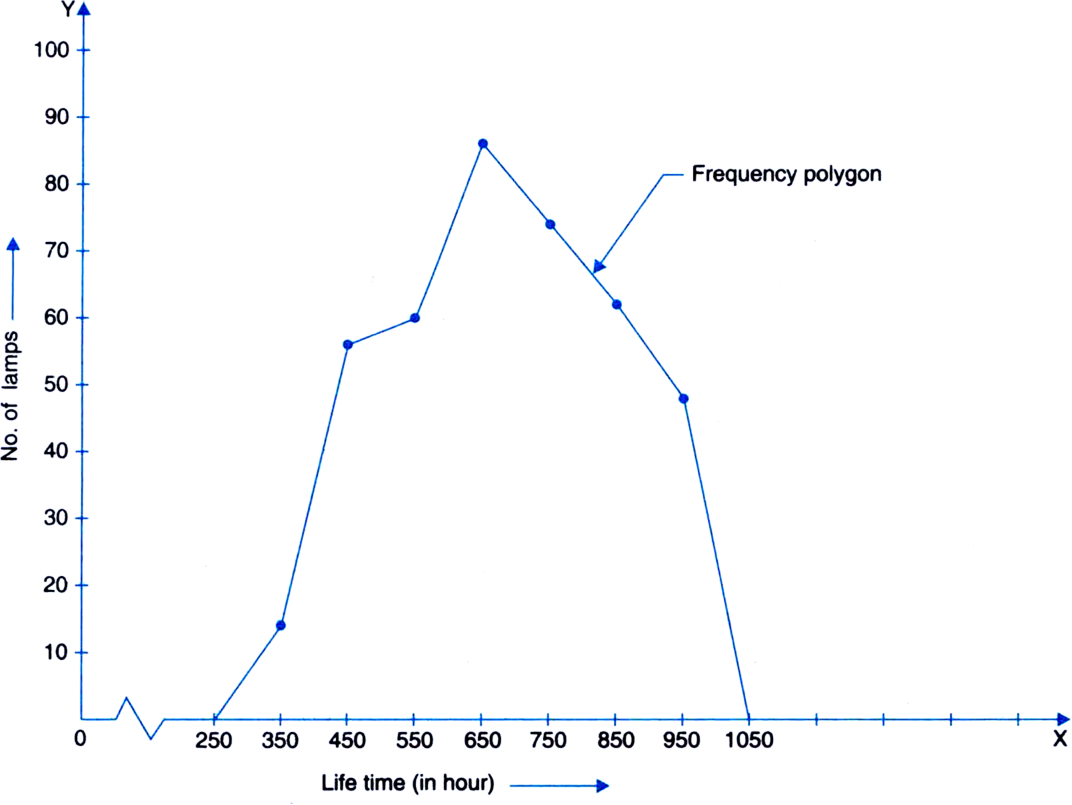
The following data gives the number (in thousands) of applicants registered with an Employment Exchange during 2005–2010.
|
Year |
No. of applicants registered (in thousand) |
|
2005 |
19 |
|
2006 |
21 |
|
2007 |
23 |
|
2008 |
30 |
|
2009 |
32 |
|
2010 |
36 |
Construct a bar graph to represent the above data.
In a particular section of Class IX, 40 students were asked about the months of their birth, the following graph was prepared for the data so obtained.
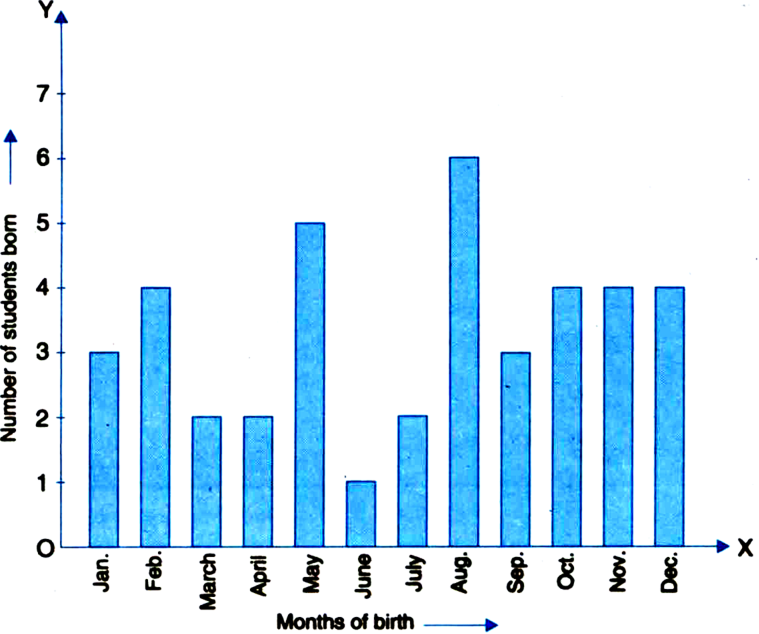
Observe the bar graph given above and answer the following questions:
(i) How many students were born in the month of November?
(ii) In which month were the maximum number of students born?
(i) 4 students were born in the month of November.
(ii) Maximum number of students were born in the month of August.
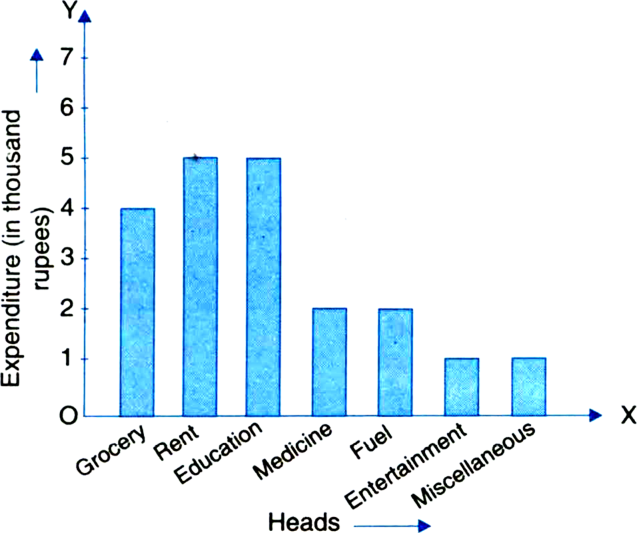
A family with monthly income of Rs. 20,000 had planned the following expenditures per month under various heads:
|
Heads |
Expenditure (in Rs. 1000) |
|
Grocery |
4 |
|
Rent |
5 |
|
Education of children |
5 |
|
Medicine |
2 |
|
Fuel |
2 |
|
Entertainment |
1 |
|
Miscellaneous |
1 |
Draw a bar graph for the data above.
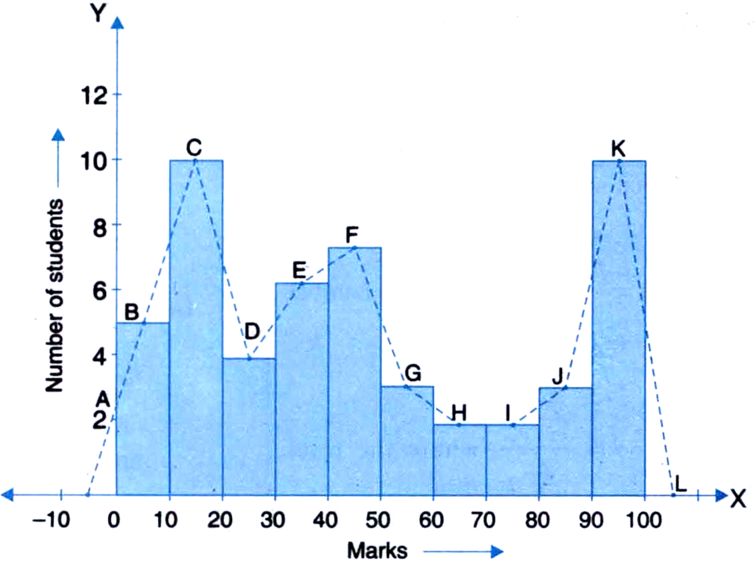
Consider the marks, out of 100, obtained by 51 students of a class in a test:
|
Marks |
Number of students |
|
0–10 |
5 |
|
10–20 |
10 |
|
20–30 |
4 |
|
30–40 |
6 |
|
40–50 |
7 |
|
50,60 |
3 |
|
60–70 |
2 |
|
70–80 |
2 |
|
80–90 |
3 |
|
90–100 |
9 |
|
Total |
51 |
Draw a frequency polygon corresponding to this frequency distribution table.
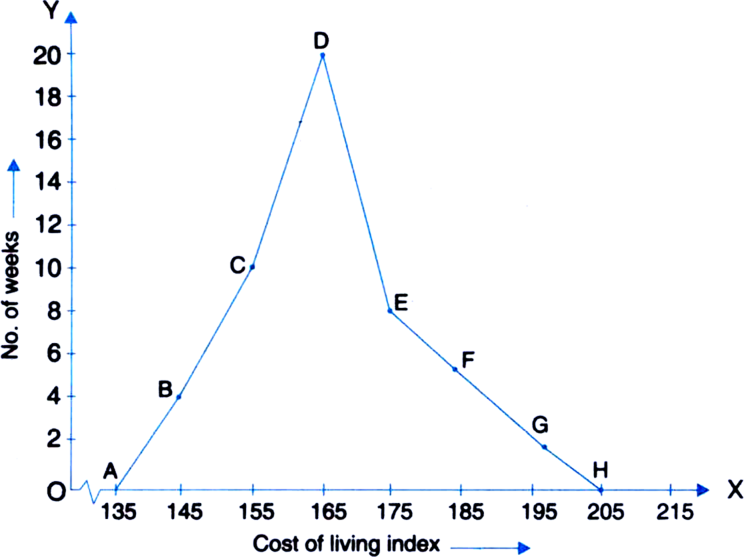
In a city, the following weekly observations were made in a study on the cost of living index:
|
Cost of living index |
Number of weeks |
|
140–150 |
5 |
|
150–160 |
10 |
|
160–170 |
20 |
|
170–180 |
9 |
|
180–190 |
6 |
|
190–200 |
2 |
|
Total |
52 |
Draw a frequency polygon for the data above (without constructing a histogram).
|
Classes |
Class marks |
Frequency |
|
140–150 |
145 |
5 |
|
150–160 |
155 |
10 |
|
160–170 |
165 |
20 |
|
170–180 |
175 |
9 |
|
180–190 |
185 |
6 |
|
190–200 |
195 |
2 |
|
Total |
52 |
The following number of goals were scored by a team in a series of 10 matches :
2, 3, 4, 5, 0, 1, 3, 3, 4, 3
Find the mean, median and mode of these scores.
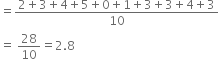
(ii) Median
Arranging the given data in ascending order, we have
0, 1, 2, 3, 3, 3, 3, 4, 4, 5
Number of observations (n) = 10, which is even.

(iii) Mode
Arranging the given data in ascending order, we have
0, 1, 2, 3, 3, 3, 3, 4, 4, 5
Here, 3 occurs most frequently (4 times)
∴ Mode = 3.
n a Mathematics test given to 15 students, the following marks (out of 100) are recorded :
41, 39, 48, 52, 46, 62, 54, 40, 96,
52, 98, 40, 42, 52, 60
Find the mean, median and mode of this data.
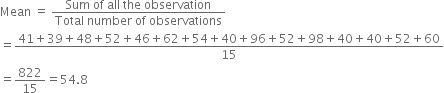
(ii) Median
Arranging the given data in descending order, we have
98, 96, 62, 60, 54, 52, 52, 52, 48,
46, 42, 41, 40, 40, 39
Number of observations (n) = 15, which is odd.
= 8th observation = 52
(iii) Mode
Arranging the data in descending order, we have
98, 96, 62, 60, 54, 52, 52, 52,
48, 46, 42, 41, 40, 40, 39
Here, 52 occurs most frequently (3 times)
∴ Mode = 52.
The following observations have been arranged in ascending order. If the median of the data is 63, find the value of x.
29, 32, 48, 50, x, x + 2, 72, 78, 84, 95

According to the question,
x + 1 = 63
Hence, the value of x is 62
Find the mode of 14, 25. 14, 28, 18, 17, 18, 14, 23, 22, 14. 18
The given data is
14, 25. 14, 28, 18, 17, 18, 14, 23, 22, 14, 18
Arranging the data in ascending order, we have
14, 14, 14, 14. 17, 18, 18, 18, 22, 23, 25, 28
Here, 14 occurs most frequently (4 times)
∴ Mode = 14.
Find the mean salary of 60 workers of a factory from the following table :
|
Salary (in Rs.) |
Number of workers |
|
3000 |
16 |
|
4000 |
12 |
|
5000 |
10 |
|
6000 |
8 |
|
7000 |
6 |
|
8000 |
4 |
|
9000 |
3 |
|
10000 |
1 |
|
Total |
60 |
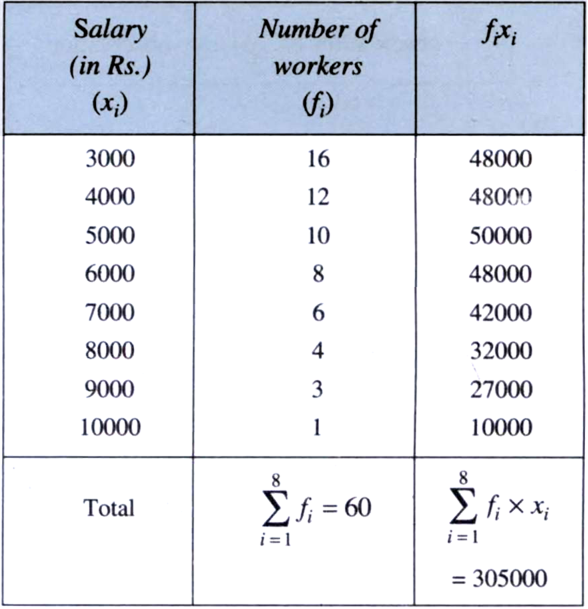
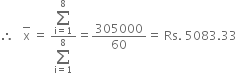
Hence, the mean salary is Rs. 5083.33.
Give one example of a situation in which
(i) the mean is an appropriate measure of central tendency
(ii) the mean is not an appropriate measure of central tendency but the median is an appropriate measure of central tendency.
(i) mean marks in a test in mathematics.
(ii) average beauty.
Find the value of p if mean of following distribution is 20.
|
X |
f |
|
15 |
2 |
|
17 |
3 |
|
19 |
4 |
|
20 + p |
5p |
|
23 |
6 |
ol.
|
x |
f |
fx |
|
15 |
2 |
30 |
|
17 |
3 |
51 |
|
19 |
4 |
76 |
|
20 + p |
5p |
5p(20 + p) |
|
23 |
6 |
138 |
|
Total |
5p + 15 |
295 + l00p + 5p2 |
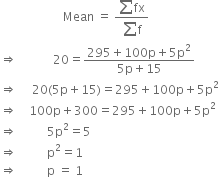
Find the mean ![]() of first ten prime numbers and hence show that
of first ten prime numbers and hence show that ![]()
First ten prime numbers are
2, 3, 7, 11, 13, 17, 19, 23, 29,31
The mean ![]()
![]()

Hence, ![]()
Find the mean of the following data:
|
x |
f |
|
10 |
3 |
|
12 |
10 |
|
20 |
15 |
|
25 |
7 |
|
35 |
5 |
Sol.
|
x |
f |
fx |
|
10 |
3 |
30 |
|
12 |
10 |
120 |
|
20 |
15 |
300 |
|
25 |
7 |
175 |
|
35 |
5 |
175 |
|
Total |
40 |
800 |
Find the mean salary of 60 workers of a factory from the table:
|
Salary per worker (in र) |
No. of workers |
|
300 |
17 |
|
400 |
13 |
|
500 |
11 |
|
600 |
9 |
|
700 |
6 |
|
800 |
4 |
|
Salary per worker (in र) xi |
No. of workers fi |
fixi |
|
300 |
17 |
5100 |
|
400 |
13 |
5200 |
|
500 |
11 |
5500 |
|
600 |
9 |
5400 |
|
700 |
6 |
4200 |
|
800 |
4 |
3200 |
|
Total |
60 |
28600 |
= र 476.66
Find the median of first ten prime numbers.
First ten prime numbers are
2, 3, 5, 7, 11, 13, 17, 19, 23, 29
n = 10 which is even![]()

The mean of 10, 12, 18, 13, x and 17 is 15. Find the value of x.
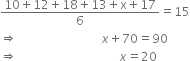
Find the mean of the following distribution:
|
x |
f |
|
4 |
5 |
|
6 |
10 |
|
9 |
10 |
|
10 |
7 |
|
15 |
8 |
l.
|
x |
f |
fx |
|
4 |
5 |
20 |
|
6 |
10 |
60 |
|
9 |
10 |
90 |
|
10 |
7 |
70 |
|
15 |
8 |
120 |
|
Total |
40 |
360 |
Find the mean of first 10 multiples of 7
First 10 multiples of 7 are
7, 14, 21, 28, 35, 42, 49, 56, 63, 70
Their mean
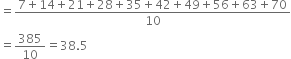
Arithmetic mean of terms 21, 16, 24, x, 29, 15 is 23. Find the value of x.
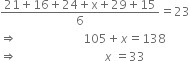
Find the mean of the following distribution:
|
Variable (x) |
Frequency (f) |
|
5 |
6 |
|
15 |
4 |
|
25 |
9 |
|
35 |
6 |
|
45 |
5 |
ol.
|
Variable (x) |
Frequency (f) |
fxx |
|
5 |
6 |
30 |
|
15 |
4 |
60 |
|
25 |
9 |
225 |
|
35 |
6 |
210 |
|
45 |
5 |
225 |
|
Total |
30 |
750 |
In the following frequency distribution, the number of students of age less than 25 years is
|
Age (in years) |
Number of students |
|
5–10 |
3 |
|
10–15 |
6 |
|
15–20 |
8 |
|
20–25 |
8 |
|
25–30 |
2 |
-
8
-
6
-
17
-
25
D.
25
In the following distribution, the number of schools with result more than 60% is
|
Result (in percent) |
Number of schools |
|
0–20 |
4 |
|
20–40 |
7 |
|
40–60 |
5 |
|
60–80 |
3 |
|
80–100 |
2 |
-
2
-
3
-
5
-
1
C.
5
In the following distribution, the number of students securing marks less than 10 is
|
Marks obtained |
Number of students |
|
0–5 |
6 |
|
5–10 |
2 |
|
10–15 |
5 |
|
15–20 |
3 |
|
20–25 |
4 |
-
8
-
7
-
6
-
5
A.
8
In the following distribution, the number of students securing marks 15 or more is
|
Marks obtained |
Number of students |
|
0–5 |
6 |
|
5–10 |
2 |
|
10–15 |
5 |
|
15–20 |
3 |
|
20–25 |
4 |
-
8
-
7
-
6
-
5
B.
7
In the following frequency distribution, what is the frequency of the variable 13?
|
x |
f |
|
3 |
3 |
|
8 |
13 |
|
13 |
6 |
|
18 |
4 |
|
23 |
5 |
|
25 |
8 |
-
3
-
4
-
6
-
5
C.
6
In the following distribution, 10 is the frequency of the variate
|
x |
f |
|
12 |
3 |
|
13 |
5 |
|
14 |
8 |
|
15 |
10 |
|
16 |
7 |
|
17 |
4 |
|
18 |
2 |
- 15
- 16
- 13
- 18
A.
15Sponsor Area
In the following frequency distribution, the lower limit of the sixth class is
|
Marks |
Number of students |
|
0–5 |
3 |
|
5–10 |
5 |
|
10–15 |
8 |
|
15–20 |
12 |
|
20–25 |
7 |
|
25–30 |
3 |
- 20
-
25
-
30
-
0
B.
25
In the following frequency distribution, the upper limit of the fourth class is
|
Daily wages (in र) |
Frequency |
|
290–325 |
5 |
|
325–360 |
2 |
|
360–395 |
4 |
|
395–430 |
6 |
|
430–465 |
7 |
|
465–500 |
5 |
- र 430
- र 395
- र 500
- र 290
A.
र 430
In a histogram, the heights of the rectangles are
-
inversely proportional to the frequencies of the corresponding classes
-
directly proportional to the frequencies of the corresponding classes
-
directly proportional to the widths of the corresponding classes
-
inversely proportional to the widths of the corresponding classes.
B.
directly proportional to the frequencies of the corresponding classesIf a frequency polygon is drawn from the following frequency distribution, then its first two points will be
|
Marks (out of 50) |
Number of students |
|
0–10 |
8 |
|
10–20 |
10 |
|
20–30 |
6 |
|
30–40 |
7 |
|
40–50 |
10 |
- (0, 0), (4, 0)
- (–5, 0), (4, 0)
-
(5, 8), (5, 10)
- (0, 0), (0, 4).
D.
(0, 0), (0, 4).If a frequency polygon is drawn from the following frequency distribution, then its last two points will be
|
Marks (out of 50) |
Number of students |
|
0–10 |
8 |
|
10–20 |
10 |
|
20–30 |
6 |
|
30–40 |
7 |
|
40–50 |
10 |
- (35, 7), (45, 10)
- (5, 50), (50, 0)
- (50, 5), (50, 0)
- (7, 35), (10, 45).
C.
(50, 5), (50, 0)
The modal value of a series is
-
middle value
-
value with maximum frequency
-
value with minimum frequency
-
limiting value
B.
value with maximum frequencyThe number of students of a school according to their age is as follows:
|
Age (in years) |
Number of students |
|
8 |
18 |
|
9 |
25 |
|
10 |
40 |
|
11 |
36 |
|
12 |
41 |
|
13 |
37 |
|
14 |
20 |
|
15 |
13 |
|
16 |
5 |
|
17 |
3 |
Their mode is
- 41
-
12
-
3
-
17
B.
12
The number of family members of 30 families of a village is according to the following table. Find their mode.
|
Number of family members |
Number of families |
|
2 |
1 |
|
3 |
2 |
|
4 |
4 |
|
5 |
6 |
|
6 |
10 |
|
7 |
3 |
|
8 |
5 |
-
6
-
5
-
7
-
4
A.
6
The marks of some students are given below. Find the mode of marks.
|
Marks |
Number of students |
|
10 |
2 |
|
20 |
8 |
|
30 |
16 |
|
40 |
26 |
|
50 |
20 |
|
60 |
16 |
|
70 |
7 |
|
80 |
4 |
- 60
-
50
-
30
-
40
D.
40
Sponsor Area
The heights (in cm) of students of a class are as follows :
155 160 145 149 150
147 152 144 148
Find the median of this data.
Solution not provided.
Ans. 149 cm
Find the mode of the following marks (out of 10) obtained by 20 students:
4, 6, 5, 9, 3, 2, 7, 7, 6, 5, 4, 9, 10, 10, 3, 4, 7, 6, 9, 9.
Solution not provided.
Ans. 9
Consider a small unit of a factory where there are 5 employees : a supervisor and four laboures. The laboures draw a salary of र 5,000 per month each while the supervisor gets र 15,000 per month. Calculate the mean, median and mode of the salaries of this unit of the factory:
5000, 5000, 5000, 5000, 15000.
Solution not provided.
Ans. र 7000 per month, र 5000 per month, र 5000 per month.
Find the mode of the following marks (out of 10) obtained by 20 students:.
10, 4, 6, 5, 9
3, 2, 10, 7, 6
5, 4, 9, 10, 10
3, 4, 10, 6, 9
Solution not provided.
Ans. 10
Find the median of the following observations:
46, 64, 87, 41, 58
77, 35, 90, 55, 92, 33
Solution not provided.
Ans. 51.5
If the mean of 16 observations is 8, and if two is added to every observation, what will be the new mean.
Solution not provided.
Ans. 10
Find the arithmetic mean of the following data:
|
x |
f |
|
1 |
5 |
|
2 |
9 |
|
3 |
12 |
|
4 |
17 |
|
5 |
14 |
|
6 |
10 |
|
7 |
6 |
Solution not provided.
Ans. 4.09
If the median of the data 12, 24, 30, 35, 37, 40, 3m, 3m + 4, 52, 57, 59, 62, 67, 70 which is arranged in ascending order, is 47, find the value of m.
Solution not provided.
Ans. 15
Find the mean of the following distribution:
|
xi |
fi |
|
10 |
7 |
|
30 |
8 |
|
50 |
10 |
|
70 |
15 |
|
90 |
10 |
Solution not provided.
Ans. 55.6
Find the median of the following data 15, 28, 72, 56, 44, 32, 31, 43 and 51. If 32 is replaced by 23, find the new median.
Solution not provided.
Ans. 43,43
The mean of five numbers is 27. If one number is excluded, their mean is 25. Find the excluded number.
Solution not provided.
Ans. 35
Find the mean of the following distribution:
|
x |
f |
|
4 |
5 |
|
6 |
10 |
|
9 |
10 |
|
10 |
7 |
|
15 |
8 |
Solution not provided.
Ans. 9
If the mean of the following data is 15, find p:
|
x |
f |
|
5 |
6 |
|
10 |
P |
|
15 |
6 |
|
20 |
10 |
|
25 |
5 |
Solution not provided.
Ans. 14
The mean of 10 numbers is 50. If one more number is ordered, then the mean is 50 itself. Find the added number.
Solution not provided.
Ans. 50
10 numbers 8, 11, 15, 19, x + 1, 2x –13, 28, 31, 40, 41 are written in ascending order. If the median is 24, find x.
Solution not provided.
Ans. 20
Mean of 50 observations was found to be 80.4. But later on it was discovered that 96 was misread as 69 at one place. Find the correct mean.
Solution not provided.
Ans. 81
Find the mode of the following data:
1, 3, 5 , 7, 3,
5, 4, 7, 2, 6,
7, 12, 10, 11, 3,
7, 8, 6, 7, 7,
4, 2, 11, 7, 15
Solution not provided.
Ans. 7
The mean of 20 observations is 50. If the observation 50 is replaced by 140, what will be the new mean of the observations?
Solution not provided.
Ans. 54.5
Find the median of the following data:
18, 37, 24, 59, 41, 56, 63, 45, 57, 29
Solution not provided.
Ans. 43
If the mean of the following data is 6, find the value of p.
|
xi |
fi |
|
2 |
3 |
|
4 |
2 |
|
6 |
3 |
|
10 |
1 |
|
p + 5 |
2 |
Solution not provided.
Ans. 7
A cricketer has a mean score of 58 runs in nine innings. Find out how many runs are to be scored in the tenth inning to raise his mean score to 61.
Solution not provided
Ans. 30
Find the mean, median and mode of the following data:
41, 39, 48, 52, 41
48, 36, 41, 37, 35
Solution not provided
Ans. 41.8; 41; 41 4.25,28
For what value of ‘x’ in the mode of the following data 7?
3, 5, 6, 7, 5, 4, 7, 6, (x + 1), 8,7
Solution not provided
Ans. 6
If the mean of x, x + 2, x + 4, x + 6, x + 8 is 24, find the value of x.
Solution not provided
Ans. 20
Find the mode of the following data:
41, 39, 48, 52, 46,
62, 54, 40, 96, 52,
98, 40, 52, 60
Find the mode of the following data:
41, 39, 48, 52, 46,
62, 54, 40, 96, 52,
98, 40, 52, 60
Solution not provided
Ans. 52
The mean of the 10 observations 15, 17, 23, 18, 17, 25, 16, 18, 20, 12 is 18. Find the value of p.
Solution not provided
Ans. 16
If the mean of five observation x, x + 2, x + 4, x + 6, x + 8 is 13, then find the value of x.
Solution not provided
Ans. 16
Determine the median of the observations 24,23, a, a – 1, 12, 16, where a is the mean of 10,20, 30, 40, 50.
Solution not provided
For a particular year, following is the distribution of ages (in hours) of primary school teachers in a particular state.
|
Age (in years) |
No. of teachers |
|
Less than 20 |
11 |
|
21–25 |
32 |
|
26–30 |
51 |
|
31–35 |
49 |
|
36–40 |
27 |
|
41–45 |
6 |
|
46–50 |
4 |
1. Determine the class limits of the fourth class.
2. What is the class size?
3. Construct a cumulative frequency table.
Solution not provided
Draw a frequency polygon for the data given below, without drawing a histogram:
|
Classes |
Frequency |
|
150–160 |
5 |
|
160–170 |
15 |
|
170–180 |
20 |
|
180–190 |
25 |
|
190–200 |
15 |
|
200–210 |
5 |
Solution not provided
The daily earning of 30 workers are given below:
|
Daily earning |
No. of workers |
|
0–50 |
3 |
|
50–100 |
7 |
|
100–150 |
4 |
|
150–200 |
5 |
|
200–250 |
4 |
|
250–300 |
3 |
|
300–350 |
2 |
|
350–400 |
2 |
Draw a histogram and a frequency polygon to represent the above data.
Solution not provided
For the following data, draw a histogram:
|
Classes |
Frequency |
|
1–4 |
6 |
|
4–6 |
30 |
|
6–8 |
44 |
|
8–12 |
16 |
|
12–20 |
4 |
Solution not provided
The distribution of weights (in kg) of 100 people is given below:
|
Weight (in kg) |
Frequency |
|
40–45 |
13 |
|
45–50 |
25 |
|
50–55 |
28 |
|
55–60 |
15 |
|
60–65 |
12 |
|
65–70 |
5 |
|
70–75 |
2 |
Construct a histogram for the above distribution.
Solution not provided
If the mean of the following data is 8, then find missing frequency p.
|
xi |
fi |
|
5 |
2 |
|
10 |
P |
|
8 |
5 |
Solution not provided
For the data 3, 21, 25, 17, (x + 3), 19, (x – 4) if mean is 18, find the value of jc and hence, find the mode of the data.
Solution not provided
The mean of five observations x, x + 2, x + 4, x + 6 and x + 8 is 23. Find the mean of last four observations.
Solution not provided
The runs scored by two teams A and B on the first 74 balls in a cricket match are given below:
|
No. of balls |
Runs scored |
|
|
Team A |
Team B |
|
|
0–12 |
10 |
4 |
|
12–24 |
12 |
2 |
|
24–36 |
4 |
16 |
|
36–48 |
20 |
18 |
|
48–60 |
10 |
8 |
|
60–72 |
12 |
10 |
|
72–84 |
6 |
12 |
Construct the frequency polygon for both teams on the same graph.
Solution not provided
Calculate mean of first 5 prime numbers.
First 5 prime numbers are 2, 3, 5, 7, 11
Their mean = ![]()
Find the mean of the following distribution:
|
Variable (x) |
Frequency (f) |
|
4 |
12 |
|
5 |
10 |
|
6 |
8 |
|
7 |
7 |
|
8 |
8 |
|
9 |
5 |
ol.
|
Variable (x) |
Frequency (f) |
fx |
|
4 |
12 |
48 |
|
5 |
10 |
50 |
|
6 |
8 |
48 |
|
7 |
7 |
49 |
|
8 |
8 |
64 |
|
9 |
5 |
35 |
|
Total |
50 |
294 |
The following observations have been arranged in ascending order. If the median of the data in 65, find the value of x.
32, 35, 50, 51, x, x + 2, 73, 76, 83, 90

Find the value of p, if the mean of the following distribution is 7.5:
x
y
3
6
5
8
7
15
9
8
11
8
13
4
Find the value of p, if the mean of the following distribution is 7.5:
|
x |
y |
|
3 |
6 |
|
5 |
8 |
|
7 |
15 |
|
9 |
8 |
|
11 |
8 |
|
13 |
4 |
|
x |
y |
xy |
|
3 |
6 |
18 |
|
5 |
8 |
40 |
|
7 |
15 |
105 |
|
9 |
P |
9p |
|
11 |
8 |
88 |
|
13 |
4 |
52 |
|
Total |
p + 41 |
9p + 303 |
Find the mode of the data 15, 14, 19, 20,14,15,16,14,15,18,14,19,15,17,15. If last observation is changed to 14, then find the new mode.
Arranging the data in the ascending order, we have,
14, 14, 14, 14, 15, 15, 15, 15, 15, 16,
17, 18, 19, 19, 20
Here, 15 occurs must frequency (5 times)
∴ Mode = 15
If the last observation is change to 14, then new data become
14, 14, 14, 14, 14, 15, 15, 15, 15, 16,
17, 18, 19, 19,20
Here, 14 occurs must frequently (5 times)
∴ New mode = 14
The mean of 200 items was 50. Later on, it was discovered that the two items were misread as 92 and 8 instead of 192 and 88. Find the correct mean.
Corrected sum = 10000 - (92 + 8) + (192 + 88)
= 10180
Marks secured by a group of 10 students are as follows:
16, 18, 29, 31, 20, 23, 26, 25, 32, 20
(i) Find the mean of the data,
(ii) If 32 is replaced by 23 in the data. find the new mean.
(iii) If each observation in the given data is increased by 5 marks, then what will be the mean?
(iv) If two students securing 16 and 32 leave the group, then find the mean of remaining 8 students.
(i) Mean
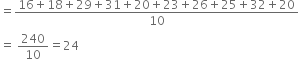
(ii) New mean
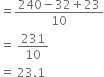
(iii) Mean = 24 + 5 = 29
(iv) Mean of remaining 8 students
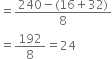
Find the mode of the observations 17, 23, 25, 18, 17, 23, 19, 23, 17, 26, 23. If 4 is subtracted from each observation, what will be the mode of the new observations?
Arranging the data in ascending order, we have,
17, 17, 18, 19, 23, 23, 23, 26
Here, 23 occurs most frequently (3 times)
∴ Mode = 23
If 4 is subtracted from each observation, then the mode of the new observations
= 23 – 4 = 19
Mock Test Series
Sponsor Area
Sponsor Area








