The following number of goals were scored by a team in a series of 10 matches :
2, 3, 4, 5, 0, 1, 3, 3, 4, 3
Find the mean, median and mode of these scores.
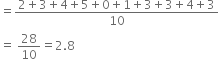
(ii) Median
Arranging the given data in ascending order, we have
0, 1, 2, 3, 3, 3, 3, 4, 4, 5
Number of observations (n) = 10, which is even.

(iii) Mode
Arranging the given data in ascending order, we have
0, 1, 2, 3, 3, 3, 3, 4, 4, 5
Here, 3 occurs most frequently (4 times)
∴ Mode = 3.



