Sponsor Area
A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30° (see Fig. 9.11)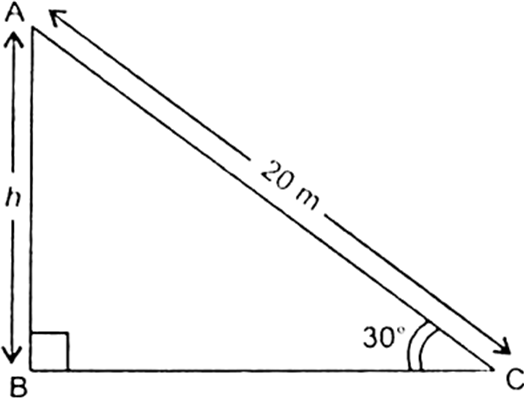
Fig. 9.11
Let AC be the rope whose length is 20 m, and AB be the vertical pole of height h m and the angle of elevation of A at point C on the ground is 30°.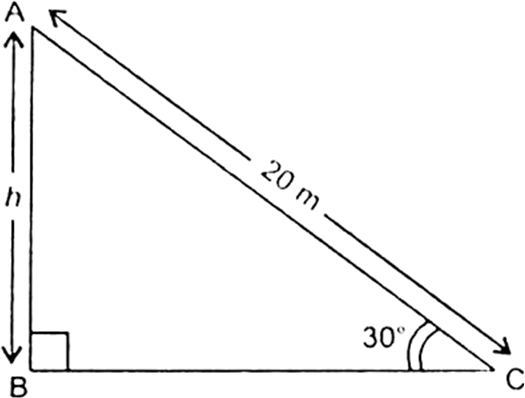
Fig. 9.11
i.e., ∠ACB = 30°
In right triangle ABC, we have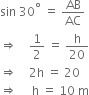
Hence, the height of the pole is 10 m.
A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
Let BD be the tree broken at point C such that the broken part CD takes the position CA and strikes the ground at A. It is given that AB = 8 m and ∠BAC = 30°.
Let BC = x metres and CD = CA = y metres
In right triangle ABC, we have
Now, height of the tree
Hence, the height of the tree 
A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 1.5 m, and is inclined at an angle of 30° to the ground, whereas for elder children, she wants to have a steep slide at a height of 3m, and inclined at an angle of 60° to the ground. What should be the length of the slide in each case?
Case I :
Calculation of length of the slide below 5 years. Fig. (a)
Let AC be the slide of length l m and height of the slide AB of height 1.5 m. It is given that slide is inclimed at an angle of 30°.
i.e., ∠ACB = 30°
In right triangle ABC, we have
Hence, the length of the slide for below 5 years is 3 m
Case II :
Calculation of the length of slide for elder children. Fig. (b)
Let DF be the slide of length m metres and DE be the height of the top of slide of height 3 m. It is given that slide is inclined at an angle of 60°.
i.e., ∠DFE = 60°
In right triangle DEF, we have
Hence, the length of the slide for elder children is 
The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower, is 30°. Find the height of the tower.
Let A be the top and B be the foot of the tower AB, of height h metre. C be the point which is 30 m away from the tower i.e. BC = 30 m.
Now,
AB = h m
BC = 30 m
and ∠ACB = 30°
In right triangle ABC, we have
Hence, the height of the tower is 
A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
Let BC be the horizontal ground, and let A be the position of the kite which is at a height of 60 m. i.e., AB = 60 m.
It is given that
∠ACB = 60°
Now, in right triangle ABC, we have
Hence, the length of string is 
Fig. 9.8.
i.e., ∠ECD = 30° and ∠EFD = 60°.
Let CF = x m and FD = y m
In right triangle EDF, we have
In right triangle EDC, we have
Comparing (i) and (ii), we get
Hence, distance (CF) 
From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60° respectively. Find the height of the tower.
Let CD be the transmission tower of height h m. fixed on a building of height 20 m.
i.e., CD = h m
and BC = 20 m.
The angles of elevation of the bottom C and top D of the transmission tower are 45° and 60° respectively.
i.e., ∠BAC = 45°
and ∠BAD = 60°
In right triangle ABC, we have
In right triangle ABD, we have
Comparing (i) and (ii) we get
Hence, height of the transmission tower is 
A statue, 1.6 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.
Let height of the pedestal BD be h metres, and angle of elevation of C and D at a point A on the ground be 60° and 45° respectively.
It is also given that the height of the statue CD be 1.6 m
i.e., ∠CAB = 60°,
∠DAB = 45° and CD = 1.6m
In right triangle ABD, we have
In right triangle ABC, we have
Comparing (i) and (ii), we get
Hence, the height of pedestal
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.
Here, ∠ABD = 60°, and ∠BAC = 30°.
Now, in right triangle ABC, we have
In right triangle BAD, we have
Comparing (i) and (ii) we get
Hence, the height of the building is 
Two poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30°, respectively. Find the height of the poles and the distances of the point from the poles.
Let AD and BC be two poles of equal height h metres. Let P be a point on the road sucn that AP = x metres. Then BP = (80 - x) metres.
It is given that ∠APD = 60° and ∠BPC = 30°.
In right triangle APD, we have
In right triangle BPC, we have
Comparing (i) and (ii), we get
Putting this value in eq. (i), we get
And, AP = x = 20 m
BP = 80 - x = 80 - 20 = 60 mHence, height of the poles 
A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point 20 m away from this point on the line joing this point to the foot of the tower, the angle of elevation of the top of the tower is 30° (see Fig. 9.12). Find the height of the tower and the width of the canal.
Fig. 9.12.
Let AB be the tower of height h metres standing on a bank of a canal. Let C be a point on the opposite bank of a canal, such that BC = x metres.
Let D be the new position after changing the elevation. It is given that CD = 20 m
The angle of elevation of the top of the tower at C and D are respectively 60° and 30°.
i.e. ∠ACB = 60° and ∠ADB = 30°
In right triangle ABC, we have
In right triangle ABD, we have
Comparing (i) and (ii), we get
Putting this value in (i), we get
Hence, the height of tower 
metres and width of the canal = 10 m.
From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower
Let AC be the building whose height is 7 m and BE be the cable tower.
It is given that the angle of elevation of the top E of the cable tower from C and the angle of depression of its foot from C be 60° and 45° respectively.
i.e., ∠DCE = 60° and ∠BCD = 45°.
Also, AC = BD = 7 m.
Let DE = h m
In right triangle DCE, we have
Now, in right triangle BCD, we have
Comparing (i) and (ii), we get
Hence, Total height of the cable lower (BE)
As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
Let AB = x m and BC = y m
In right triangle BCD, we have
In right triangle ACD, we have
Comparing (i) and (ii) we get
Hence, the distane between two ships be 
A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°. After some time, the angle of elevation reduces to 30° (see Fig. 9.13). Find the distance travelled by the balloon during the interval.
Fig. 9.13.
⇒ Distance travelled by the balloon
EF = GC = AC - AG
= (150.68 - 50.23) m
= 100.45 metres.
A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower from this point.
It is given that the angle of depression at A and B from the top of a tower be 30° and 60° respectively.
Let the speed of the car be v second per minute. Then
AB = distance travelled by the car in 6 s.
= (6 × v) sec. (Dist = speed × time)
= 6v sec.
Let the car takes t minutes to reach the tower CD from B.
Then,
BC = distance travelled by car in t minutes
= (v × t) metres = vt sec.
In right triangle BCD, we have
In right triangle ACD, we have
Comparing (i) and (ii), we get
Hence, the time taken by the car to reach the foot of the tower is 3 sec.
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.
Let ∠BDA = ө, then ∠BCA = (90 - ө)
In right triangle BCA, we have
In right triangle BDA, we have
Multiplying (i) and (ii) we get
Since, h = -6 is not possible
Hence, height of the tower BC is 6 m.
Sponsor Area
Let the height of the pole AB = x m.
∴ Length of shadow OB ol the pole AB = x m.
Let the angle of elevation be ө, i.e.
∠AOB = ө
In Right triangle OBA, we have
Hence, the angle of elevation of the Sun's altitude is 45°.
Let O be a point be a point 20 m away from the tower AB = hm
In right triangle OBA, we have
thus, th height of the tower is 
Lenght of string OA = 100 m.
Angle of elevation = 60°. Let the heigth of the kite be AB = h m.
In right triangle OBA, we have
Thus, the height of the kite is 
Let AC the cable which is inclined at 60° to the horizontal
Here, we have
AC = 215 m and ∠ACB = 60°
Now, In right triangle ACB.
AQ = x m and BQ = y m and the angle of elevation of the top of the tree P from point A and B are 30° and 45° respectively.
i.e., ∠PAQ = 30° and ∠PBQ = 45°
In right triangle
AQP, we have
In right triangle BQP, we have
Adding (i) and (ii), we get
find the speed of the jet plane.
Putting the value of (i) in (ii), we get
1500 + BD = 4500
⇒ BD = 3000
∵ Distance travelled in 15 sec
= CE = BD = 3000 metres,
Now, speed of plane (m/s) = 
and speed of plane (km/h) = 
= 720 km/hr
metres.
Let AB be the tower of height h metres, D and C are two points on the horizontal line, which are at distances a and b metres respectively from the base of the tower. It is also given that the angles of elevation of the top of a tower from two points D and C be complementary i.e.,
∠ADB = Ս then ∠ACB = (90 -ө)
In right triangle ADB, we have
In right triangle ACB, we have
Multiplying (i) and (ii), we get
But height can't be negative.
Hence the height of the tower is 
mts.
Let QR = x m
In right triangle QRY, we have
In right triangle QPX, we have
Comparing (i) and (ii), we get
So, height of the tower PQ
= PR + QR
= 40 + x
= 40 + 54.64
= 94.64 m.
In right triangle QPX, we have
⇒ 3h = h + 9
⇒ 3h - h = 9
⇒ 2h = 9
⇒ h = 4.5 m
Now, height of the tower
= (h + 9) met.
= (4.5 + 9) met.
= 13.5 met.
Difference between the building and tower (x)
Height of lighthouse = 100 m
Let distance travelled by the ship, when the angle of depression changes from 60° to 30° (DC) =y m and distance BC = x m Then, in right ∆ABC,
In right 
ABD, tan 
From (i) and (ii), we get
Hence, distance travelled by the ship = 115.473 m.
Tips: -
Let CD be the hill of height h km. Let A and B be two stones due east of the hill at a distance of 1 km. from each other. It is also given that the angles of depression of. stones A and B from the top of a hill be 30° and 45° respectively.
Let BC = x km
In right triangle BCD, we have
In right triangle ACD, we have
Comparing (i) and (ii), we get
Hence, the height of hill is 1.365.
Let C and D be the position of two aeroplanes. The height of the aeroplane which is at point D be 3000 m and it passes another aeroplane vertically which is at point C. Let BC = x m. It is also given that the angles of elevation of two planes from the point A on the ground is 45° and 60° respectively.
In right triangle ABC, we have
In right triangle ABD, we have
]
Comparing (i) and (ii), we get
Hence, vertical distance between the aeroplane
= CD = BD - BC
Let CD be the flagstaff whose height is 7 m, fixed on the tower BC of height h metres. From a point A on the ground the angles of elevation of top and bottom of the flagstaff are 45° and 30° respectively.
In right triangle ABC, we have
In right triangle ABD, we have
Comparing (i) and (ii), we get
Hence, the height of the tower = 9.56 m.
Let CD be the tree of height h m. Let B be the position of a man standing on the opposite bank of the river. After moving 40 m away from point B let new position of man be A i.e., AB = 40 m.
The angles of elevation of the top of the tree from point A and B are 30° and 60° respectively, i.e., ∠CAD = 30° and ∠CBD = 60°. Let BC = x m.
In right triangle BCD, we have
In right triangle ACD, we have
Comparing (i) and (ii), we get
Hence, the height of the tree is 34.64 metres. Now substituting the value of
Hence, the width of the river is 20 m.
Let PM be perpendicular from P on CB. Then, ∠CPM = 30° and ∠CPM = 60°.
Let CM = h. Then, CB = h + 100 and CB = h + 100.
In right 
CMP,
In right 
PMC'
From (i) and (ii), we get
Now, CB = CM + MB = h + 100 = 100 + 100 = 200
Hence, the height of the helicopter from the surface of the lake = 200 m
Let AB = x metres.
In right triangle ABD, we have
In right triangle ABC, we have
Comparing (i) and (ii), we get
Sponsor Area
Let AB be the surface of the lake and P be the position of the observer h metres above the lake. Let C be the cloud and C be the reflection in the cloud, then CB = C'B. It is also given that the angle of elevation of cloud from a point h m above a lake is α and angle of depression of its reflection is β.
i.e., ∠CPQ = α
and ∠QPC' = β.
Let CQ = x m
Then
CB = CQ + BQ
= CQ + PA
= x + h
In right triangle PQC, we have
In right triangle PQC', we have
Comparing (i) and (ii), we get
Hence, the height of the cloud
Hence, the height of the cloud is
Let height of the centre C be h m and CA = CB = r
In right triangle CBP, we have
et AB be the surface of the lake and 'P' be the position of the observer h metres above the lake. Let C be the cloud and C' be the reflection in the cloud. Then CB = C'B. It is also given that the angle of elevation of cloud from a point h m above a lake is α and angle of depression of its reflection be β. i.e., ∠CPQ = α and ∠QPC' = β. Let CQ = xm.
In right triangle PQC, we have
In right triangle PQC, we have
In right triangle PQC', we have
Comparing (ii) and (iii), we get
Comparing (i) and (iv), we get
Hence, the distance of the cloud from the point of observer is 
Let D be the vertical position of the aeroplane of height h mile i.e., CD = h miles. Let A and B are the position of two stones on opposite sides of the aeroplane which are at a distances of 1 mile from each other. It is also given that the angles of depression of these stones from the aeroplane are α and β respectively.
i.e., ∠CAD = α and ∠CBD = β
Let AC = x then BC = 1-x
In right triangle ACD, we have
In right triangle BCD, we have
Comparing (i) and (ii), we get
Hence, the height of the aeroplane above the road in miles be 
.
metres.
i.e., ∠ABD = α and ∠ACD = β
Let BD = x m and CD = y m
In right triangle ABD, we jave
In right triangle ACD, we have
Adding (i) and (ii), we get
Hence, the distance between the ship is 
metres.
.
Let BC be the ladder which slides down a distance b on the wall.
In right triangle ABC, we have
So, replacing AE by ED sin β, we get 
As, BC and ED both represent the same ladder.
BC = ED. (length of ladder does not change)
⇒ BC sin α - BC sin β = b
⇒ BC (sin α - sin β) = b ...(i)
Similarly, in right triangle AED, we have
So, by replacing AC by BC cos α, we get ED cos β = BC cos α + a BC (cos . - cos α) = a [∴ ED = BC] ...(ii) Dividing (ii) by (i), we get
i.e., ∠DCE = ө
and ∠BCD - φ.
Let DE = x m
In right triangle CDE, we have
In right triangle BCD, we have
Comparing (i) and (ii), we get
Hence, height of the opposite house (BE)
= BD + DE
= h + x
= h + h cot φ . tan ө
= h (1 + cot φ . tan ө).
Also, determine the height of the tower if p = 50 metres, α = 60°, β = 30°.
i.e., ∠BDA = β and ∠BCA = α
In right triangle ABC, we have
In right triangle ABD, we have
Comparing (i) and (ii), we get
Case II : p = 50 m, α = 60°, β = 30°.
= 20 x 1.732 = 43.25 m.
Hence, height of the tower is 43.25 m.
i.e., ∠CAE = ө. ∠CAF = φ and AF = k metres. From F draw FD and FB perpendiculars on CE and AC respectively. It is also given that ∠DFE = α.
In right triangle ABF, we have
In right triangle ACE, we have
And, DE = CE - CD = CE - BF
= h - k sin φ.
In right triangle DFE, we have
Hence, the height of the cliff is
Let CE be the leaning tower. Let A and B be two given stations at distances a and b respectively from the foot of the tower.
Let CD = x and DE = h
In right triangle CDE, we have
In right triangle BDE, we have
In right triangle ADE, we have
Comparing (i) and (ii), we get
Comparing (i) and (iii), we get
Comparing (iv) and (v), we get
Hence, inclination ө to the horizontal is given by cot 
The angle of elevation of top of the pole from point A on the ground be 60° and the angle of depression of the point A from the top of the tower be 45°, i.e. ∠ BAD = 60° and ∠ BAC = 45°.
In right triangle ABC, we have
In right triangle ABD, we have
Find the height of the lighthouse.
Let BD = x m and CD = y m.
In right triangle ABD, we have
In right triangle ACD, we have
Adding (i) and (ii), we get
Hence, the height of the light house = 200 m.
Let D be the position of second boy and DF be the length of second kite. It is given ∠EDF = 45°.
In right triangle DEF, we have
Hence, the length of the string = 
Let C be position of the man. AB be the water level, and BH be the hill. The angles of elevation of the top and depression of foot from the deck of the ship be 60° and 30° respectively.
i.e., ∠DCH = 60° and ∠BCD = 30°
Let HD = x m
In right triangle CDH, we have
In right triangle CDB, we have
Hence, distance of the ship from the hill 
Comparing (i) and (ii), we get
Now, total height of the hill
= BD + DH = 10 + x
= 10 + 30 = 40 m
Hence, height of the hill = 40 m.
i.e., ∠ACB = β
and ∠ADB = α
Let BC = x metres
In right triangle ABC, we have
In right triangle ABD, we have
Comparing (i) and (ii), we get
Hence, the height of the tower be 180 mts.
AD and BE are two towers. The angle of depression of 1st tower (AD), when seen from the top of 2nd tower (BE) is 30°.
i.e., ∠CDE = 30°.
It is given that
AD = 60 m
and AB = CD = 140 m.
Let height of 2nd tower BE be h metres.
In right triangle CDE, we have
Hence, the height of the second tower is 140.83 m.
Let A be the position of boy D, be the position of girl and F be the position of kite, such that AF - 100 m; CD = 20 m; ∠BAF = 30° and ∠EDF = 45°
In right triangle ABF, we have
Let DF be the length of the second kite.
Now, in right triangle DEF, we have
Hence, the length of te string = 
Hence, the usual speed of the aircraft be x km/hr = 750 km/hr.
Let CD be the building such that CD = 100 m.
Let AB be the tower of height h metre. It is given that the angles of depression of the top A and the bottom B of the lower AB are 45° and 60° respectively.
i.e., ∠EAC = 45° and ∠DBC = 60°
Let BD = AE = x
In right triangle AEC, we have
In right triangle BDC, we have
Comparing (i) and (ii), we get
Hence,Height of tower (AB) = 42.26 m.
We have ∠PBD = 30° and ∠PAC = 45°
Let PD = h and AC = BD = x
Now, in 
BPD, tan 300 = 
Comparing (i) and (ii), we gel
Now, total height of mullistroycd building
And distance between two buildings(x)
Let AB be the first pole such that AB = 60 m. Let the weight of the second pole be n metre. It is given that the angles of depression of the top A and the bottom B of the pole AB are 30° and 60° respectively.
∴ ∠ACE = 30° and ∠ADB = 60°
Let BD = EC = x
Now, in right triangle ACE, we have
In right triangle ADB, we have
⇒ x = 20 × 1.732 = 34.64 m
Hence, width of the river = 34.64 m.
Comparing (i) and (ii), we gel
Hence,height of other pole = 40 m.
Let AC be the Tower such that AC = 40 m and BE be tine light house. Let CD be the horizontal from C. It is given that angles of elevation of the top of the light house from top and foot of the tower be 30° and 60° respectively.
i.e., ∠DCE = 30° and ∠BAE = 60°
Let AB = CD = x m and DE = x m
Now, in right triangle CDE, we have tan 30°
In right triangle ABE, we have
Comparing (i) and (ii), we gel
Hence,heighl of light house = BD + DE = 40 + 20 = 60 m.
In right triangle ABE, we have sin 60 
Hence, the distance of the top of the light house from the foot of the tower is 
Let hetght of the pedestal BD be h metres, and angle of elevation of C and D at a point A on the ground be 60° and 45° respectively.
It is also given that the height of tine statue CD be 1.6 m
i.e., ∠CAB = 60°,
∠DAB = 45° and CD = 1.6m
In right triangle ABD, we have
In right triangle ABC, we have
Comparing (i) and (ii), we get
Hence, the height of pedestal
= 0.73 (1.73 + 1) = 0.73 × 2.73
= 1.929 m. = 2 m. (approx)
Tips: -
Tips: -
Let the height of the pole AB = x m.
∴ Length of shadow OB ol the pole AB = x m.
Let the angle of elevation be ө, i.e.
∠AOB = ө
In Right triangle OBA, we have
Hence, the angle of elevation of the Sun's altitude is 45°.
Let O be a point be a point 20 m away from the tower AB = hm
In right triangle OBA, we have
thus, th height of the tower is 
Lenght of string OA = 100 m.
Angle of elevation = 60°. Let the heigth of the kite be AB = h m.
In right triangle OBA, we have
Thus, the height of the kite is 
Let AC the cable which is inclined at 60° to the horizontal
Here, we have
AC = 215 m and ∠ACB = 60°
Now, In right triangle ACB.
m away from the foot of a tower, the angle of elevation of the top of the tower is 30°. Find the height of tow'er.
Sponsor Area
Tips: -
m long, from a point at a distance of 100 m, from the foot of the lower in a horizontal plane.
Sponsor Area
A ladder leaning against a wall makes an angle of 60° with the horizontal. If the foot of the ladder is 2.5 m away from the wall, find the length of the ladder.
Let AB be the ladder and CA be the wall.
The ladder makes an angle of 60o with the horizontal.
Given: BC = 2.5 m, ∠ABC = 60°
AB = 5 cm and ∠BAC = 30°
From Pythagoras Theorem, we have
AB2 = BC2 + CA2
52 = (2.5)2 + (CA)2
(CA)2 = 25 – 6.25 = 18.75 m
Hence, length of the ladder is 
A man standing on the deck of a ship, which is 10 m above water level, observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of a hill as 30°. Find the distance of the hill from the ship and the height of the hill.
Let CD be the hill and suppose the man is standing on the deck of a ship at point A.
The angle of depression of the base C of the hill CD observed from A is 30° and the angle of elevation of the top D of the hill CD observed from A is 60°.
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60o. From a point Y, 40 m vertically above X, the angle of elevation of the top Q of the tower is 45o. Find the height of the tower PQ and the distance PX. 
Given the angle of elevation of the top Q of a vertical tower from the PQ from a point X on the ground is 60o.
From a point Y, 40 m vertically above X, the angle of elevation of the top Q of the tower is 45o.
In Given figure, a tower AB is 20 m high and BC, its shadow on the ground, is m 
long. Find the sun's altitude.
Let the sun's altitude be θ.
In ΔABC,
, find the speed of the plane in km/hr.
Prove that tangents drawn at the ends of a diameter of a circle are parallel to each other.
Let AB be the diameter of a circle, with centre O. The tangents PQ and RS are drawn at points A and B, respectively.
We know that a tangent at any point of a circle is perpendicular to the radius through the point of contact.
∴ OA ⊥ PQ and OB ⊥ RS
⇒ ∠OBR = 90°
∠OBS = 90°
∠OAP = 90°
∠OAQ = 90°
We can observe the following:
∠OBR = ∠OAQ and ∠OBS = ∠OAP
Also, these are the pair of alternate interior angles.
Since alternate interior angles are equal, the lines PQ and RS are parallel to each other.
Hence, proved.
In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA = 12 cm, QC = QD = 3 cm, then find PC + PD.
Given: PA and PB are the tangents to the circle.
PA = 12 cm
QC = QD = 3 cm
To find: PC + PD
PA = PB = 12 cm
(The lengths of tangents drawn from an external point to a circle are equal)
Similarly, QC = AC = 3 cm
and QD = BD = 3 cm.
Now, PC = PA − AC = 12 − 3 = 9 cm
Similarly, PD = PB − BD = 12 − 3 = 9 cm
Hence, PC + PD = 9 + 9 = 18 cm.
Two tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that ∠PTQ = 2 ∠OPQ.
Given: TP and TQ are two tangents of a circle with centre O and P and Q are points of contact
To prove: ∠PTQ=2∠OPQ
Suppose ∠PTQ=θ.
Now by theorem, "The lengths of tangents drawn from an external point to a circle are equal".
So, TPQ is an isosceles triangle.
Therefore, ∠TPQ=∠TQP= 
Also by theorem "The tangents at any point of a circle is perpendicular to the radius through the point of contact" ∠OPT=90°.
Therefore,
∠OPQ=∠OPT−∠TPQ
Hence, ∠PTQ=2∠OPQ.
Prove that the lengths of tangents drawn from an external point to a circle are equal.
Proof: We know that a tangent to the circle is perpendicular to the radius through the point of contact.
∴ ∠OPT = ∠OQT = 90°
In ΔOPT and ΔOQT,
OT = OT (Common)
OP = OQ (Radius of the circle)
∠OPT = ∠OQT (90°)
∴ ΔOPT ≅ ΔOQT (RHS congruence criterion)
⇒ TP = TQ (CPCT)
Hence, the lengths of the tangents drawn from an external point to a circle are equal.
A chord PQ of a circle of radius 10 cm subtends an angle of 60° at the centre of the circle. Find the area of major and minor segments of the circle.
Radius of the circle, r = 10 cm
Area of sector OPRQ
In ΔOPQ,
∠OPQ = ∠OQP (As OP = OQ)
∠OPQ + ∠OQP + ∠POQ = 180°
2∠OPQ = 120°
∠OPQ = 60°
ΔOPQ is an equilateral triangle.
So, area of ΔOPQ
Area of minor segment PRQ
= Area of sector OPRQ − Area of ΔOPQ
= 52.33 − 43.30
= 9.03 cm2
Area of major segment PSQ
= Area of circle − Area of minor segment PRQ
=π(10)2−9.03=314−9.03=304.97 cm2
Prove that the lengths of tangents drawn from an external point to a circle are equal.
Construction: Draw a circle centred at O.
If the difference between the circumference and the radius of a circle is 37cm, then using , the circumference (in cm) of the circle is:
154
44
14
7
B.
44
Let r be the radius of the circle,
From the given information, we have
In a circle of radius 21 cm, an arc subtends an angle of at the centre.Find: (i) the length of the arc (ii) area of the sector formed by the arc.
The arc subtends an angle of 60
In fig., a circle with centre O is inscribed in a quadrilateral ABCD such that, it touches the sides BC, AB, AD and CD at points P, Q, R and S respectively, If AB = 29 cm, AD = 23 cm, B = 90o and DS = 5 cm, then the radius of thecircle (in cm) is
11
18
6
15
A.
11
Given: Ab, BC,CD,and AD tangents to the circle with centre O at
Q,P,S and R respectively.
AB=29 cm, AD=23 cm, DS=5 cm and B=900
Construction: Join PQ.
We know that, the lengths of the tangents drawn from an external
point to a circle are equal.
DS=DR=5 cm
AR= AD - DR= 23 cm- 5 cm= 18 cm
AQ=AR= 18 cm
QB = AB - AQ = 29 cm - 18 cm= 11 cm
QB = BP = 11 cm
In
In fig., PA and PB are two tangents drawn from an external point P to a circlewith centre C and radius 4 cm. If PA PB, then the length of each tangent is
3
4
5
6
B.
4
Therefore, APBC is a square having side equal to 4 cm.
Therefore, length of each tangent is 4 cm.
Two circular pieces of equal radii and maximum area, touching each otherare cut out from a rectangular card board of dimensions 14 cm x 7 cm. Find the area of the remaining card board.
Dimensions of the rectangle card board = 14 cm x 7 cm
Since, two circular pieces of equal radii and maximum area touching each other are cut from the rectangular card board, therefore, the diameter oa each of each circular pieces is
The incircle of an isosceles triangle ABC, in which AB = AC, touches the sides BC, CA and AB at D, E and F respectively. Prove that BD = DC.
Given: is an isosceles triangle with a circle inscribed in the triangle.
To prove: BD=DC
Proof:
AF and AE are tangents drawn to the circle from point A.
Since two tangents drwan to a circle from the same exterior point are equal.
AF=AE=a
Similarly BF=BD=b and CD=CE=c
We also know that is an isosceles triangle
Thus AB=AC
a+b=a+c
Thus b=c
Therefore, BD=DC
Hence proved.
Prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
Given: A circle C ( 0, r ) and a tangent l at point A.
To prove: OA l
Construction: Take a point B, other than A, on the tangent l. Join OB. Suppose OB meets the circle in C.
Proof: We know that, among all line segment joining the point O to a point on l, the perpendicular is shortest to l.
OA = OC (Radius of the same circle)
Now, OB = OC + BC.
But among all the line segments, joining the point O to a point on AB, the shortest one is the perpendicular from O on AB.
Hence OA is perpendicular to l.
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Let ABCD be a quadrilateral circumscribing a circle centered at O such that it touches the circle at point P, Q, R, S.
Let us join the vertices of the quadrilateral ABCD to the center of the circle.
AP = AS (Tangents from the same point)
OP = OS (Radii of the same circle)
OA = OA ( common side )
Hence, opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
If the angle between two tangents drawn from an external point P to a circle of radius a and centre O, is 60°, then find the length of OP.
In the figure, PA and PB are two tangents from an external point P to a circle with centre O and radius = a
A circle touches all the four sides of a quadrilateral ABCD. Prove that
AB + CD = BC + DA
Since tangents drawn from an external point to a circle are equal in length, we have
AP = AS ........(i)
BP = BQ ........(ii)
CR = CQ ........(iii)
DR = DS ........(iv)
Adding (i), (ii), (iii), (iv), we get
AP + BP + CR + DR = AS + BQ + CQ + DS
( AP + BP ) + ( CR + DR ) = ( AS + DS ) + ( BQ + CQ )
Prove that the tangents drawn at the end points of a chord of a circle make equal angles with the chord.
Let AB be a chord of circle with centre O.
Let AP and BP be two tangents at A and B respectively.
Suppose the tangents meet at point P. Join OP.
Suppose OP meets AB at C.
In the given figure, XY and X’Y’ are two parallel tangents to a circle with centre O and another tangents AB with point of contact C, is intersecting XY at A and X’Y’ at B. Prove that ∠AOB = 90°.
Since tangents drawn from an external point to a circle are equal.
Therefore, AP = AC.
Thus, in triangles AOP and AOC, we have
AP = AC
AO = AO ..........[Common side]
OP = OC ..........[ Radii of the same circle ]
So, by SSS- criterion of congruence,
We have,
Similarly, we can prove that
Prove that the lengths of two tangents drawn from an external point to a circle are equal.
Given: AP and AQ are two tangents from a point A to a circle c(0,r)
To prove: AP = AQ
construction: Join OP, OQ and OA.
Proof:
Hence, by RHS- criterion of congruence, e have
In Fig., the sides AB, BC and CA of a triangle ABC, touch a circle at P, Q and R respectively. If PA = 4 cm, BP = 3 cm and AC = 11 cm, then the length of BC (in cm) is
11
10
14
15
B.
10
it is know that the lengths of tangents drwan from a point outside a circle
are equal in length.
Therefore, we have;
AP = AR ........(1) (Tangents drawn from point A)
BP = BQ .........(2) (Tangents drawn from point B)
CQ = CR ..........(3) (Tangents drawn from point C)
Using the above equations,
AR = 4 cm ( AP = 4 cm, given)
BQ = 3 cm ( BP = 3 cm, given)
AC = 11 cm RC = 11 cm - 4 cm = 7 cm
Hence, BC = BQ + CQ = 3 CM + 7 CM = 10 cm.
In Fig., a circle touches the side DF of EDF at H and touches ED and EF produced at K and M respectively. If EK = 9 cm, then the perimeter of EDF (in cm) is:
18
13.5
12
9
A.
18
It is known that the tangents from an external point to the circle are equal.
EK = EM, DK = DH and FM = FH .....(1)
Perimeter of EDF = ED + DF + FE
= (EK - DK) + (DH + HF) + EM - FM)
= (EK - DH) + (DH + HF) + (EM - FH) [Using (1)]
= EK + EM
= 2EK = 2(9 CM) = 18 CM
Hence, the perimeter of EDF is 18 cm.
Tangents PA and PB are drawn from an external point P to two concentric circle with centre O and radii 8 cm and 5 cm respectively, as shown in Fig., If AP = 15 cm, then find the length of BP.
Given: Tangents PA and PB are drwan from an external point P to two
concentric circles with centre O and radii OA = 8 cm, OB = 5 cm
respectively. Also, AP = 15 cm.
Construction: We join the points O and P.
Proof: OA AP ; OB BP
[ Using the property that radius is perpendicular to the tangent at the
point of contact of a circle.]
In right angled triangle OAP,
OP2 = OA2 + AP2 [ Using pythagoras theorem ]
= (8)2 + ( 15 )2 = 64 + 225 = 289
OP = 17 cm
In right angled triangled OBP,
OP2 = OB2 + BP2
BP2 = OP2 - OB2
(17)2 - (5)2
289 - 25
= 264
BP = = 2 cm.
In fig., an isosceles triangle ABC, with AB =AB, circumscribes a circle. Prove that the point of contact P bisects the base BC.
OR
In fig., the chord AB of the larger of the two concentric circles, with centre O, touches the smaller circle at C. Prove that AC = CB.
Given: ABC is an isosceles triangle, where AB = AC, circumscribing a circle.
To prove: The point of contact P bisects the base BC, i.e. BP = PC
Proof: It can be observe that
BP and BR; CP and CQ; AR and AQ; are pairs of tangents drawn to the circle
from the external points B, C, and A respectively.
Since the tangents drawn from an external point to a circle, then
BP = BR ............(i)
CP = CQ ............(ii)
AR = AQ ............(iii)
Given that AB = AC
AR + BR = AQ + CQ
BR = CQ .........[ From (iii) ]
BP = CP .........[From (i) and (ii) ]
P bisects BC.
OR
Given: The chord AB of the larger of the two concentric circles, with centre O,
touches the smaller circle ar C.
To prove: AC = CB
Construction: Let us join OC.
Proof: In the smaller circle, AB is a tangent to the circle at the point of contact C.
OC AB .....................(i)
( Using the property that the radius of a circle is perpendicular to the tangent at the point of contact )
For the larger circle, AB is a chord and from (i) we have OCAB
OC bisects AB
( Using the property that the perpendicular drawn from the centre to a chord of a circle bisects the chord.)
AC = CB.
Prove that the parallelogram circumscribing a circle is a rhombus.
OR
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Let ABCD be a parallelogram such that its sides touching a circle with centre O.
We know that the tangents to a circle from an exterior point are equal in length.
AP = AS .......[Tangnts from point A] .......(i)
BP = BQ .......[Tangents from point B] .......(ii)
CR = CQ .......[Tangents from point C] .......(iii)
and, DR = DS .......[Tangents from point D] ........(iv)
Adding (i), (ii), (iii), and (iv), we get
AP + BP + CR + DR = AS + BQ + CQ + DS
(AP + BP) + (CR + DR) = ( AS + DS) + (BQ + CQ)
AB + CD = AD + BC
2AB = 2BC [ ABCD is a parallelogram AB = CD and BC = AD]
AB = BC
Thus, AB = BC = CD = AD
Hence, ABCD is a rhombus.
OR
A circle with centre O touches the sides AB, BC, CD and DA of a quadrilateral
ABCD at the points P, Q, R and R respectively.
To prove:
Construction: Join OP, OQ, OR and OS.
Proof: Since the two tangents drawn from a external point to a circle
subtend equal angles at the centre.
Hence proved.
Prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
OR
A quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB + CD = AD + BC.
Given: AB is tangent to a circle with centre O.
To prove: OP is perpendicular to AB.
Constructions: Take a point Q on AB and join OQ.
Proof: Since Q is a point on the tangent AB, other than the point of contact P, so Q will be outside the circle.
Let OQ intersect the circle at R.
Now OQ = OR + RQ
Thus OP is shorter than any other segment among all and the shortest length is the perpendicular from O on AB.
Hence proved.
OR
Let ABCD be a quadrilateral, circumscribing a circle.
Since the tangents drawn to the circle from an external point are equal,
we have,
AP = AS ..........(1)
BP = BQ ..........(2)
RC = QC ..........(3)
DR = DS ..........(4)
Adding, (1), (2), (3) and (4), we get
AP + PB + RC + DR = AS + BQ + QC + DS
(AP + PB ) + (RC + DR ) = (AS + DS ) + (BQ + QC)
AB + CD = AD + BC.
Sponsor Area
Sponsor Area
.
find the speed in km/hr, of the plane.
(d) 
(c) 
(d) 30 m
