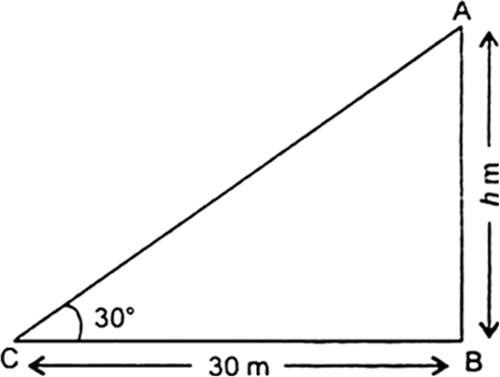
The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower, is 30°. Find the height of the tower.

Solution

Let A be the top and B be the foot of the tower AB, of height h metre. C be the point which is 30 m away from the tower i.e. BC = 30 m.
Now,
AB = h m
BC = 30 m
and ∠ACB = 30°
In right triangle ABC, we have
$tan space 30 degree space equals space AB over BC$

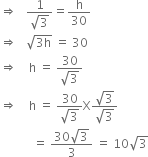
$rightwards double arrow space space space fraction numerator 1 over denominator square root of 3 end fraction equals straight h over 30 rightwards double arrow space space space square root of 3 straight h end root space equals space 30 rightwards double arrow space space space space straight h space equals space fraction numerator 30 over denominator square root of 3 end fraction rightwards double arrow space space space space straight h space equals space fraction numerator 30 over denominator square root of 3 end fraction straight X fraction numerator square root of 3 over denominator square root of 3 end fraction space space space space space space space space space space space equals space fraction numerator 30 square root of 3 over denominator 3 end fraction space equals space 10 square root of 3$
Hence, the height of the tower is $10 square root of 3 space straight m.$

For Daily Free Study Material Join wiredfaculty

Circles

The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower, is 30°. Find the height of the tower.

Some More Questions From Circles Chapter

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

Phone Number

Email Address

Loaction