Question
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.
Solution
Let BC be the height of the building of height h m. and AD be the tower of height 50 m.
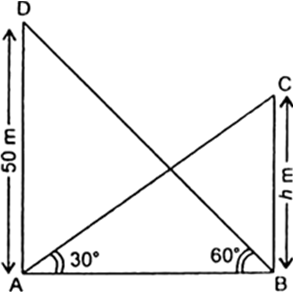

Here, ∠ABD = 60°, and ∠BAC = 30°.
Now, in right triangle ABC, we have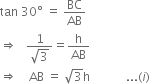
In right triangle BAD, we have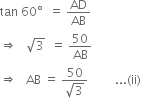
Comparing (i) and (ii) we get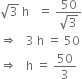
Hence, the height of the building is ![]()



