Mathematics Chapter 13 Surface Areas And Volumes
Sponsor Area
NCERT Solution For Class 9 About 2.html
Construct an angle of 90° at the initial point of a given ray and justify the construction.
Given: A ray OA.
Required: To construct an angle of 90° at O and justify the construction.
Steps of Construction:
1. Taking O as centre and some radius, draw an arc of a circle, which intersects OA, say at a point B.
2. Taking B as centre and with the same radius as before, draw an are intersecting the previously drawn are, say at a point C.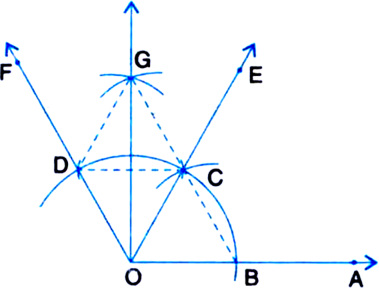
3. Taking C as centre and with the same radius as before, draw an arc intersecting the arc drawn in step 1, say at D.
4. Draw the ray OE passing through C. Then ∠EOA = 60°.
5. Draw the ray OF passing through D. Then ∠FOE = 60°.
6. Next, taking C and D as centres and with the radius more than ![]() ID, draw arcs to intersect each other, say at G.
ID, draw arcs to intersect each other, say at G.
7. Draw the ray OG. This ray OG is the bisector of the angle ∠FOE, i.e., ∠FOG![]()
Justification:
(i) Join BC.
Then. OC = OB = BC (By construction)
∴ ∆COB is an equilateral triangle.
∴ ∠COB = 60°.
∴ ∠EOA = 60°.
(ii) Join CD.
Then, OD = OC = CD (By construction)
∴ ∆DOC is an equilateral triangle.
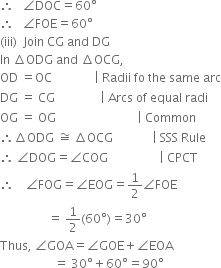
Construct an angle of 45° at the initial point of a given ray and justify the construction.
Given: A ray OA.
Required: To construct an angle of 45° at O and justify the construction.
Steps of Construction:
1. Taking O as centre and some radius, draw an arc of a circle, which intersects OA, say at a point B.
2. Taking B as centre and with the same radius as before, draw an arc intersecting the previously drawn arc, say at a point C.
3. Taking C as centre and with the same radius as before, draw an arc intersecting the arc drawn in step 1, say at D.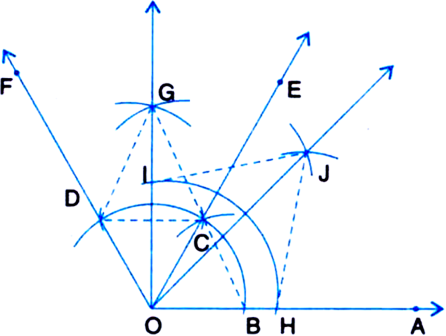
4. Draw the ray OE passing through C. Then ∠EOA = 60°.
5. Draw the ray OF passing through D. Then ∠FOE = 60°.
6. Next, taking C and D as centres and with radius more than ![]() CD, draw arcs to intersect each other, say at G.
CD, draw arcs to intersect each other, say at G.
7. Draw the ray OG. This ray OG is the bisector of the angle FOE, i.e., ∠FOG![]()
8. Now, taking O as centre and any radius, draw an arc to intersect the rays OA and OG. say at H and I respectively.
9. Next, taking H and I as centres and with the radius more than ![]() HI, draw arcs to intersect each other, say at J.
HI, draw arcs to intersect each other, say at J.
10. Draw the ray OJ. This ray OJ is the required bisector of the angle GOA.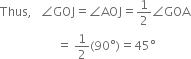
Justification:
(i) Join BC.
Then, OC = OB = BC (By construction)
∴ ∆COB is an equilateral triangle.
∴ ∠COB = 60°.
∴ ∠EOA = 60°.
(ii) Join CD.
Then, OD = OC = CD (By construction)
∴ ∆DOC is an equilateral triangle.
∴ ∠DOC = 60°.
∴ ∠FOE = 60°.
(iii) Join CG and DG.
In ∆ODG and ∆OCG,
OD = OC | Radi fo the same arc
DG = CG | Arcs of equal radii
OG = OG | Common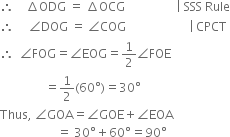
(iv) Join HJ and IJ![]()
OI = OH | Radii of the same arc
IJ = HJ | Arcs of equal radii
OJ=OJ | Common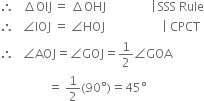
Construct the angles of the following measurements:

(i) 30°
Given: A ray OA.
Required: To construct an angle of 30° at O.
Steps of Construction:
1. Taking O as centre and some radius, draw an arc of a circle, which intersects OA, say at a point B.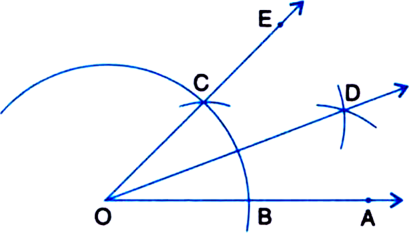
2. Taking B as centre and with the same radius as before, draw an arc intersecting the previously drawn arc, say at a point C.
3. Draw the ray OE passing through C. Then ∠EOA = 60°.
4. Taking B and C as centres and with the radius more than ![]() BC, draw arcs to intersect each other, say at D.
BC, draw arcs to intersect each other, say at D.
5. Draw the ray OD. This ray OD is the bisector of the angle EOA, i.e.,
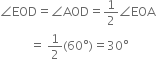
Construct the angles of the following measurements:
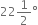
Given : A rayOA
Required : To construct an angle of
Steps of Construction:
1. Taking O as centre and some radius, draw an arc of a circle, which intersects OA, say at a point B.
2. Taking B as centre and with the same radius as before, draw an arc intersecting the previously drawn arc, say at a point C.
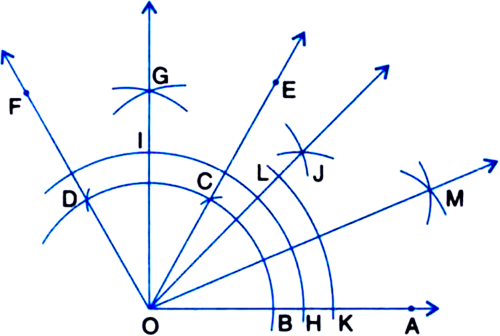
3. Taking C as centre and with the same radius as before, draw an arc intersecting the arc drawn in step 1, say at D.
4. Draw the ray OE passing through C. Then ∠EOA = 60°.
5. Draw the ray OF passing through D. Then ∠FOE = 60°.
6. Next, taking C and D as centres and with radius more than ![]() CD, draw arcs to intersect each other, say at G.
CD, draw arcs to intersect each other, say at G.
7. Draw the ray OG. This ray OG is the bisector of the angle FOE, i.e.,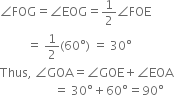
8. Now, taking O as centre and any radius, draw an arc to intersect the rays OA and OG, say at H and I respectively.
9. Next, taking H and I as centres and with the radius more than ![]() HI, draw arcs to intersect each other, say at J.
HI, draw arcs to intersect each other, say at J.
10. Draw the ray OJ. This ray OJ is the bisector of the angle GOA.
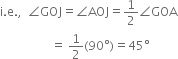
11. Now, taking O as centre and any radius, draw an arc to intersect the rays OA and OJ, say at K and L respectively.
12. Next, taking K and L as centres and with the radius more than ![]() KL, draw arcs to intersect each other, say at M.
KL, draw arcs to intersect each other, say at M.
13. Draw the ray OM. This ray OM is the bisector of the angle AOJ, i.e., ∠JOM = ∠AOM![]()
Construct the angles of the following measurements:
15°
15°
Given: A ray OA.
Required: To construct an angle of 15° at O.
Steps of Construction:
1. Taking O as centre and some radius, draw an arc of a circle, which intersects OA, say at a point B.
2. Taking B as centre and with the same radius as before, draw an arc intersecting the previously drawn arc, say at a point C.
3. Draw the ray OE passing through C.
Then ∠EOA = 60°.
4. Now, taking B and C as centres and with the radius more than ![]() BC, draw arcs to intersect each other, say at D.
BC, draw arcs to intersect each other, say at D.
5. Draw the ray OD intersecting the arc drawn in step 1 at F. This ray OD is the bisector of the angle EOA, i.e., ∠EOD = ∠AOD![]()
6. Now, taking B and F as centres and with the radius more than ![]() BF, draw arcs to intersect each other, say at G.
BF, draw arcs to intersect each other, say at G.
7. Draw the ray OG. This ray OG is the bisector of the angle AOD, i.e., ∠DOG =
![]()
Construct the following angles and verify by measuring them by a protractor:
75°
(i) 75°
Given: A ray OA.
Required: To construct an angle of 75° at O.
Steps of Construction:
1. Taking O as centre and some radius, draw an arc of a circle, which intersects OA, say at a point B.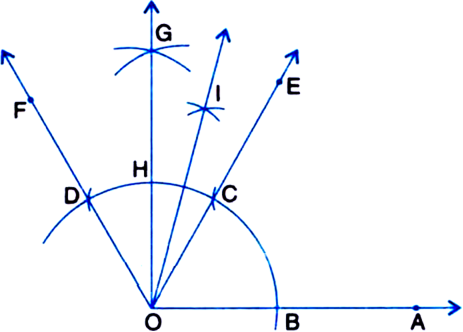
2. Taking B as centre and with the same radius as before, draw an arc intersecting the previously drawn arc, say at a point C.
3. Taking C as centre and with the same radius as before, draw an arc intersecting the arc drawn in step 1, say at D.
4. Join the ray OE passing through C. Then ∠EOA = 60°.
5. Draw the ray OF passing through D. Then ∠FOE = 60°.
6. Next, taking C and D as centres and with the radius more than ![]() CD, draw arcs to intersect each other, say at G.
CD, draw arcs to intersect each other, say at G.
7. Draw the ray OG intersecting the arc of step 1 at H. This ray OG is the bisector of the intersect each other, say at G. 7. Draw the ray OG intersecting the arc of step 1 at H. This ray OG is the bisector of the angle FOE, 
8. Next, taking C and H as centres and with the radius more than ![]() CH, draw arcs to intersect each other, say at I.
CH, draw arcs to intersect each other, say at I.
9. Draw the ray OI. This ray OI is the bisector of the angle GOE, 
On measuring the ∠IOA by protractor, we find that ∠IOA = 15°.
Thus the construction is verified.
Construct the following angles and verify by measuring them by a protractor:
105°
105°
Given: A ray OA.
Required: To construct an angle of 105° at O.
Steps of Construction:
1. Taking O as centre and some radius, draw an arc of a circle, which intersects OA, say at a point B.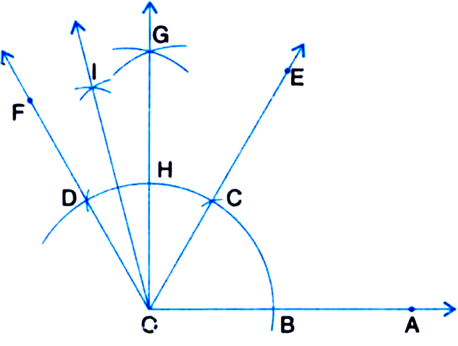
2. Taking B as centre and with the same radius as before, draw an are intersecting the previously drawn arc, say at a point C.
3. Taking C as centre and with the same radius as before, draw an arc intersecting the arc drawn in step 1, say at D.
4. Draw the ray OE passing through C. Then ∠EOA = 60°.
5. Draw the ray OF passing through D. Then ∠FOE = 60°.
6. Next, taking C and D as centres and with the radius more than ![]() CD, draw arcs to intersect each other, say at G.
CD, draw arcs to intersect each other, say at G.
7. Draw the ray OG intersecting the arc drawn in step 1 at H. This ray OG is the bisector of the angle FOE, 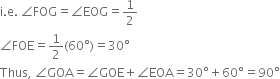
8. Next, taking H and D as centres and with the radius more than ![]() HD, draw arcs to intersect each other, say at I. 9. Draw the ray OI. This ray OI is the bisector of the angle FOG,
HD, draw arcs to intersect each other, say at I. 9. Draw the ray OI. This ray OI is the bisector of the angle FOG, 
Thus, ∠IOA = ∠IOG + ∠GOA = 15° + 90° = 105°. On measuring the ∠IOA by protractor, we find that ∠IOA = 105°.
Thus, the construction is verified.
Construct the following angles and verify by measuring them by a protractor:
135°
135°
Given: A ray OA.
Required: To construct an angle of 135° at O. Steps of Construction:
1. Produce AO to A' to form ray OA'.
2. Taking O as centre and some radius, draw an arc of a circle, which intersects OA at a point B and OA' at a point B'.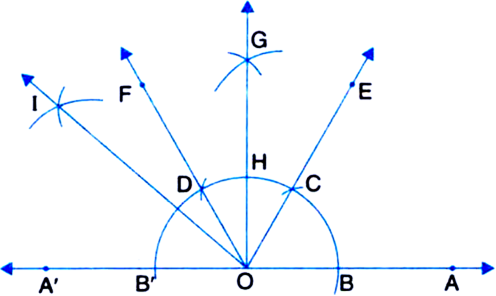
3. Taking B as centre and with the same radius as before, draw an arc intersecting the previously drawn arc at a point C.
4. Taking C as centre and with the same radius as before, draw an arc intersecting the arc drawn in step 1, say at D.
5. Draw the ray OE passing through C.
Then ∠EOA = 60°.
6. Draw the ray OF passing through D.
Then ∠FOE = 60°.
7. Next, taking C and D as centres and with the radius more than ![]() CD, draw arcs to intersect each other, say at G.
CD, draw arcs to intersect each other, say at G.
8. Draw the ray OG intersecting the arc drawn in step 1 at H. This ray OG is the bisector of the angle FOE, 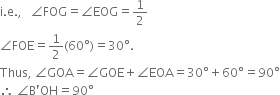
9. Next, taking B' and H as centres and with the radius more than the radius more than ![]() B'H, draw arcs to intersect each other, say at I.
B'H, draw arcs to intersect each other, say at I.
10. Draw the ray OI. This ray 01 is the bisector of the angle B'OG, i.e., ∠B'OI = ∠GOI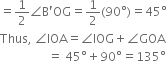
On measuring the ∠IOA by protractor, we find that ∠IOA = 135°.
Thus, the construction is verified.
Construct an equilateral triangle, given its side and justify the construction.
Given: Side (say 6 cm) of an equilateral triangle.
Required: To construct the equilateral triangle and justify the construction.
Steps of Construction:
1. Take a ray AX with initial point A. From AX, cut off AB = 6 cm.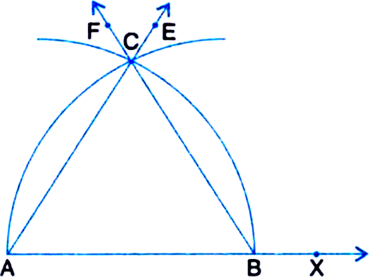
2. Taking A as centre and radius (= 6 cm), draw an arc of a circle, which intersects AX, say at a point B.
3. Taking B as centre and with the same radius as before, draw an arc intersecting the previously drawn arc, say at a point C.
4. Draw the ray AE passing through C.
5. Draw the ray BF passing through C. Then ∆ABC is the required triangle with given side 6 cm.
Justification:
AB = BC | By construction
AB = AC | By construction
∴ AB = BC = CA
∴ AABC is an equilateral triangle.
∴ The construction is justified.
Construct an equilateral triangle with one side 6 cm.
Steps of Construction
1. Draw BC = 6 cm.
2. With B as centre and 6 cm as radius, draw an arc on one side of BC.
3. With C as ccntre and 6 cm as radius, draw another arc on the same side of BC to intersect the former arc at A.
4. Joint AB and AC.
Then, ∆ABC is the required equilateral triangle.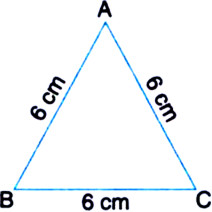
Draw a line segment AB = 5 cm. From the point A draw a line segment AD = 6 cm making an angle of 60°. Draw perpendicular bisector of AD.
Steps of Construction
1. Draw a line segment AB = 5 cm.
2. Taking A as centre and some radius, draw an arc of a circle, which intersects AB, say at a point P.
3. Taking P as centre and with the same radius as before, drawn an arc intersecting the previously draw arc, say at a point E.
4. Draw the ray AC passing through E.
5. From ray AC, cut off AD = 6 cm.
Then, ∠DAB is the required angle of 60° such that AD = 6 cm.
6. Now, taking A and D as centres and radius more than ![]() AD, draw arcs on both sides of the line segment AD (to intersect each other).
AD, draw arcs on both sides of the line segment AD (to intersect each other).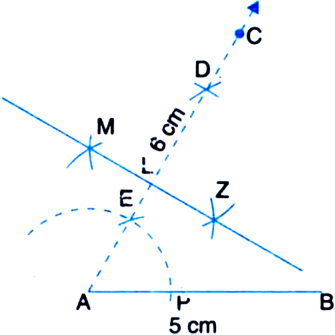
7. Let these arcs intersect each other at M and N. Join MN.
8. Let MN intersect AD at the point L. Then line MLN is the required perpendicular bisect or of AD.
Draw a line segment of 10 cm. Divide it into four equal parts. Write the measure of each part.
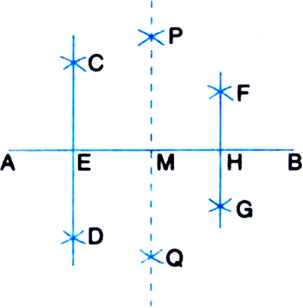
1. Draw a line segment AB = 10 cm.
2. Taking A and B as centres and radius more than ![]() AB, draw arcs on both sides of the line segment AB (to intersect each other).
AB, draw arcs on both sides of the line segment AB (to intersect each other).
3. Let these arcs intersect each other at P and Q. Join PQ.
4. Let PQ intersect AB at the point M.
5. Taking A and M as centres and radius more than ![]() AM, draw arcs on both sides of the line segment AM (to intersect each other).
AM, draw arcs on both sides of the line segment AM (to intersect each other).
6. Let these arcs intersect each other at C and D. Join CD.
7. Let CD intersect AM at the point E.
8. Taking M and B as centres and radius more than ![]() MB, draw arcs on both sides of the line segment MB (to intersect each other).
MB, draw arcs on both sides of the line segment MB (to intersect each other).
9. Let these arcs intersect each other at F and G Join FG.
10. Let FG intersect MB at H.
Then, AE = EM = MH = HB, i.e., AE, EM, MH and HB are the four equal parts. By measurement,
AE = EM = MH = HB = 2.5 cm
Construct an equilateral triangle LMN, one of whose sides is 5 cm. Bisect ∠M of the triangle.
Steps of Construction
1. Draw a line segment MN = 5 cm.
2. With M as centre and 5 cm as radius, draw an arc on one side of MN.
3. With N as centre and 5 cm as radius, draw another arc on the same side of MN to intersect the former arc at L.
4. Join LM and LN.
Then, ∆LMN is the required equilateral triangle.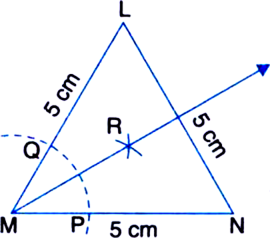
5. Taking M as centre and any radius, draw an arc to intersect the line segments MN and ML at P and Q respectively.
6. Next, taking P and Q as centres and with the radius more than ![]() PQ, draw arcs to intersect each other, say at R. 7. Draw the ray MR. This ray MR is the required bisector of the ∠M.
PQ, draw arcs to intersect each other, say at R. 7. Draw the ray MR. This ray MR is the required bisector of the ∠M.
Construct an angle ∠BAC = 90° on a line segment AB = 6 cm. Cut AC = 5 cm. Bisect AC at D. Measure AD and DC.
Steps of Construction
1. Draw a line segment AB = 6 cm.
2. Taking A as centre and some radius, draw an arc of a circle, which intersects AB, say at a point P.
3. Taking P as centre and with the same radius as before, draw an arc intersecting the previously drawn arc, say at a point Q.
4. Taking Q as centre and with the same radius as before, drawn an arc intersecting the arc drawn in step 1, say at R.
5. Next, taking Q and R as centres and with the radius more than ![]() QR, draw arcs to intersect each other, say at S.
QR, draw arcs to intersect each other, say at S.
6. Draw the ray AS.
7. From ray AS, cut off AC = 5 cm.
Then. ∠BAC = 90° is such that AB = 6 cm and AC = 5 cm.
8. Taking A and C as centres and radius more than ![]() AC. draw arcs on both sides of the line segment AC (to intersect each other).
AC. draw arcs on both sides of the line segment AC (to intersect each other).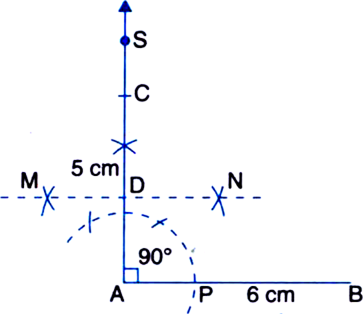
9. Let these arcs intersect each other at M and N. Join MN.
10. Let MN intersect AC at the point D.
Then, AD = DC
By measurement,
AD = DC = 2.5 cm
Draw an acute angled triangle ABC. Construct perpendicular bisectors of AB and BC intersecting each other at O. Measure OA, OB and OC. Are they equal?
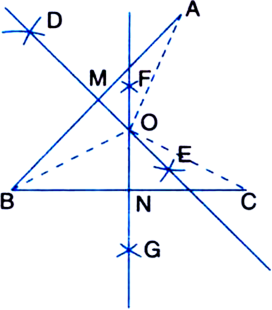
1. Draw an acute angled triangle ABC.
2. Taking B and A as centres and radius more than ![]() BA, draw arcs on both sides of the line segment BA (to intersect each other).
BA, draw arcs on both sides of the line segment BA (to intersect each other).
3. Let these arcs intersect each other at D and E. Join DE.
4. Let DE intersect BA at the point M. Then line DME is the required bisector of BA.
5. Again, taking B and C as centres and radius more than ![]() BC, draw arcs on both sides of the line segment BC (to intersect each other).
BC, draw arcs on both sides of the line segment BC (to intersect each other).
6. Let these arcs intersect each other at F and G Join FG.
7. Let FG intersect BC at the point N. Then line FNG is the required bisector of BC.
8. Let the bisectors DME and FNG intersect each other at O.
By measure,
OA = OB = OC = 3.8 cm
Draw an angle of 40° with a protractor and then construct an angle 80° using ruler and compass.
Steps of Construction
1. Draw an angle AOC = 40° with a protractor.
2. Taking O as centre and some radius, draw an arc of a circle, which intersects OA at P and OB at Q.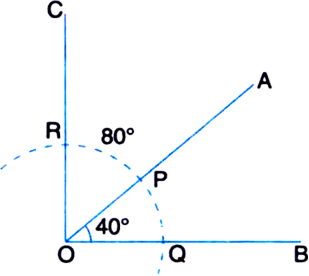
3. Taking P as centre and radius QP. draw an arc of a circle, which intersects the arc drawn in step 2, say at a point R.
4. Join OQ and produce to form a ray OC. Then, ∠COB = 80°
Construct an angle of 120° at the initial point of a given ray and justify the construction.
Solution not provided.
Sponsor Area
Construct an angle of 150° at the initial point of a given ray and justify the construction.
Solution not provided.
Using scale and compass, construct an equilateral triangle with one side as 4 cm and justify the construction.
Solution not provided.
Construct an equilateral triangle of side 6.6 cm. Label its vertices as A, B and C. From point C draw a median CF.
Solution not provided.
Construct a ∆ABC with ∠A = 75°, ∠B = 30° and AB = 5.6 cm. Measure ∠C.
Solution not provided.
Construct a triangle ABC in which BC = 7 cm, ∠B = 75° and AB + AC = 13 cm.
Given: In AABC, BC = 7 cm, ∠B = 75° and AB + AC = 13 cm.
Required: To construct the triangle ABC.
Steps of Construction:
1. Draw the base BC = 7 cm.
2. At the point B make an angle XBC = 75°.
3. Cut a line segment BD equal to AB + AC (= 13 cm) from the ray BX.
4. Join DC.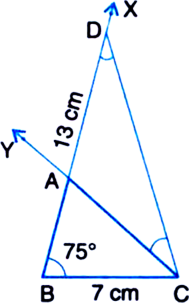
5. Make an ∠DCY = ∠BDC.
6. Let CY intersect BX at A.
Then, ABC is the required triangle.
Construct a triangle ABC in which BC = 8 cm, ∠B = 45° and AB – AC = 3.5 cm.
Given: In ∆ABC, BC = 8 cm, ∠B = 45° and AB – AC = 3.5 cm.
Required: To construct the triangle ABC.
Steps of Construction:
1. Draw the base BC = 8 cm.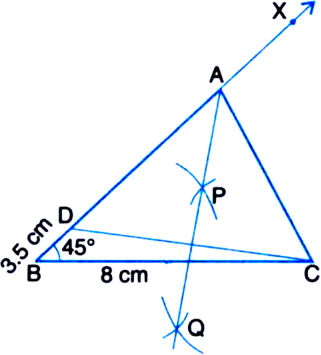
2. At the point B make an angle XBC = 45°.
3. Cut the line segment BD equal to AB – AC (= 3.5 cm) from the ray BX.
4. Join DC.
5. Draw the perpendicular bisector, say PQ of DC.
6. Let it intersect BX at a point A.
7. Join AC.
Then, ABC is the required triangle.
Construct a triangle PQR in which QR = 6cm, ∠Q = 60° and PR – PQ = 2cm.
Given: In ∆PQR, QR = 6 cm, ∠Q = 60° and PR – PQ = 2 cm.
Required: To construct the ∆PQR.
Steps of Construction:
1. Draw the base QR = 6 cm.
2. At the point Q make an ∠XQR = 60°.
3. Cut line segment QS = PR – PQ (= 2 cm) from the line QX extended on opposite side of line segment QR.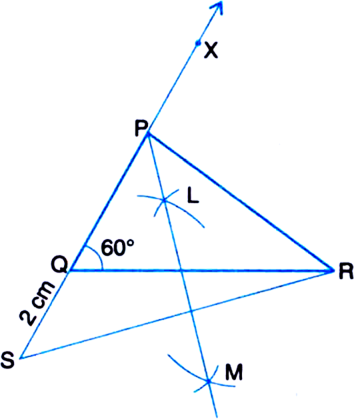
4. Join SR.
5. Draw the perpendicular bisector LM of SR.
6. Let LM intersect QX at P.
7. Join PR.
Then, PQR is the required triangle.
Construct a triangle XYZ in which ∠Y = 30°, ∠Z = 90° and XY + YZ + ZX = 11 cm.
Given: In triangle XYZ, ∠Y = 30°, ∠Z = 90° and XY + YZ + ZX = 11 cm.
Required: To construct the ∆XYZ.
Steps of Construction:
1. Draw a line segment BC = XY + YZ + ZX (= 11 cm).
2. Make ∠LBC = ∠Y (= 30°) and ∠MCB = ∠Z (= 90°).
3. Bisect ∠LBC and ∠MCB. Let these bisectors meet at a point X.
4. Draw perpendicular bisectors DE of XB and FG of XC.
5. Let DE intersect BC at Y and FG intersect BC at Z.
6. Join XY and XZ.
Then, XYZ is the required triangle.
Construct a right triangle whose base is 12 cm and sum of its hypotenuse and other side is 18 cm
Given: In right ∆ABC, base BC = 12 cm, ∠B = 90° and AB + AC = 18 cm.
Required: To construct the right triangle ABC.
Steps of Construction:
1. Draw the base BC = 12 cm.
2. At the point B, make an ∠XBC = 90°.
3. Cut a line segment BD = AB + AC (= 18 cm) from the ray BX.
4. Join DC.
5. Draw the perpendicular bisector PQ of CD to intersect BD at a point A.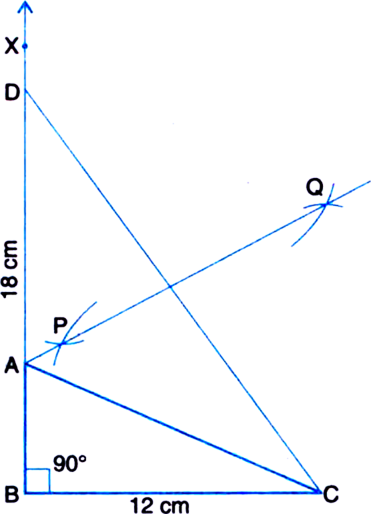
6. Join AC.
Then, ABC is the required right triangle.
Construct a triangle ABC in which ∠B = 60°, ∠C = 45° and AB + BC + CA = 11 cm.
Solution not provided.
Construct a triangle ABC in which BC = 4.6 cm, ∠B = 45° and AB + AC = 8.2 cm.
Solution not provided.
Construct a right triangle whose base is 3.5 cm and sum of its hypotenuse and other side is 5.5 cm.
Solution not provided.
Construct a triangle ABC in which BC = 4.5 cm, ∠B = 45° and AB – AC = 2.5 cm.
Solution not provided.
Construct a triangle ABC is which BC = 5 cm, ∠B = 30° and AC – AB = 2 cm.
Solution not provided.
Construct a triangle ABC is which BC = 5 cm, ∠B = 30° and AC – AB = 2 cm.
Solution not provided.
Construct a triangle PQR in which ∠Q = 45°, ∠R = 60° and PQ + QR + RP = 20 cm.
Solution not provided.
Construct a ∆XYZ in which ∠Y = 45°, ∠Z = 30° and XY + YZ + ZX = 10 cm.
Solution not provided.
Construct a triangle ABC in which BC = 8 cm, ∠B = 30° and AB – AC = 3.5 cm.
Solution not provided.
Construct a ∆ABC, in which BC = 4.7 cm, ∠B = 60° and AB + BC = 8.2 cm.
Solution not provided.
Sponsor Area
Construct a triangle PQR such that ∠R = 75°, ∠Q = 45° and PQ + QR + RP = 11 cm.
Solution not provided.
Construct a triangle ABC in which ∠A = 60°, ∠B = 90° and AB + BC + CA = 11 cm.
Solution not provided.
Construct a right angled triangle whose perimeter is equal to 10 cm and one acute angle is 60°.
Solution not provided.
Construct a triangle ABC in which BC = 3.4 cm, AB – AC = 1.5 cm and ∠B = 45°.
Solution not provided.
Construct a triangle ABC in which ∠B = 45°, ∠C = 90° and AB + BC + CA = 10 cm.
Solution not provided.
Construct a ∆ABC in which BC = 3.4 cm, AB – AC = 1.5 cm and ∠B = 30°.
Solution not provided.
Construct a right angled triangle whose base is 4 cm and sum of its hypotenuse and other side is 8 cm.
Solution not provided.
Construct a triangle PQR in which QR = 7 cm, ∠Q = 45° and PQ – PR = 4 cm.
Solution not provided.
Construct a triangle ABC in which BC = 6 cm, ∠B = 75°, AB + AC = 14 cm.
Solution not provided.
Construct a triangle ABC, in which ∠B = 60°, ∠C = 45°, AB + BC + CA = 18 cm.
Solution not provided.
Construct a triangle ABC in which ∠B = 45°, ∠C = 60° and AB + BC + CA = 12 cm.
Solution not provided.
Construct a triangle ABC in which BC = 7 cm, ∠B = 75° and AB + BC = 13 cm.
Solution not provided.
Construct a triangle ABC in which BC = 8 cm, ∠B = 60° and AB – AC = 2.5 cm.
Solution not provided.
Construct a triangle PQR, in which QR = 7 cm, measure of angle Q = 45° and PQ – PR = 3 cm.
Solution not provided.
Construct a triangle ABC in which BC = 4 cm, ∠B = 45° and AB – AC = 1.5 cm.
Solution not provided.
Construct a triangle XYZ, in which ∠Y = 60°, ∠Z = 90°, and the perimeter of the triangle XYZ is 18 cm.
Solution not provided.
Construct a ∆ABC, in which BC = 5 cm, ∠C = 60° and AC – AB = 1.5 cm.
Solution not provided.
Construct a right triangle ABC, right angled at B, in which BC = 4 cm and AC + AB = 8 cm.
Solution not provided.
Construct a ∆ABC, in which ∠B = 60°, ∠C = 45°and AB + BC + CA = 10 cm.
Solution not provided.
Construct a triangle in which base is 4.1 cm, base angle is 45° and sum of other two sides is 6.7 cm.
Solution not provided.
Construct a ∆ABC, in which base BC = 4.5 cm, ∠C = 45°and sum of sides AB and AC is 8 cm. Justify your construction.
Solution not provided.
Draw AB = 6 cm. Construct an angle of 30° at A and also draw the perpendicular bisector of AB.
Solution not provided.
Mock Test Series
Sponsor Area
Sponsor Area





