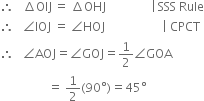Construct an angle of 45° at the initial point of a given ray and justify the construction.

Given: A ray OA.
Required: To construct an angle of 45° at O and justify the construction.
Steps of Construction:
1. Taking O as centre and some radius, draw an arc of a circle, which intersects OA, say at a point B.
2. Taking B as centre and with the same radius as before, draw an arc intersecting the previously drawn arc, say at a point C.
3. Taking C as centre and with the same radius as before, draw an arc intersecting the arc drawn in step 1, say at D.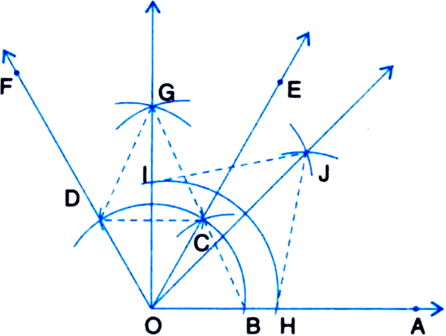

4. Draw the ray OE passing through C. Then ∠EOA = 60°.
5. Draw the ray OF passing through D. Then ∠FOE = 60°.
6.  Next, taking C and D as centres and with radius more than  CD, draw arcs to intersect each other, say at G.
7.  Draw the ray OG. This ray OG is the bisector of the angle FOE, i.e., ∠FOG

8. Now, taking O as centre and any radius, draw an arc to intersect the rays OA and OG. say at H and I respectively.
9.  Next, taking H and I as centres and with the radius more than  HI, draw arcs to intersect each other, say at J.
10. Draw the ray OJ. This ray OJ is the required bisector of the angle GOA.

Justification:
(i) Join BC.
Then, OC = OB = BC (By construction)
∴ ∆COB is an equilateral triangle.
∴ ∠COB = 60°.
∴ ∠EOA = 60°.
(ii) Join CD.
Then, OD = OC = CD (By construction)
∴ ∆DOC is an equilateral triangle.
∴ ∠DOC = 60°.
∴ ∠FOE = 60°.
(iii) Join CG and DG.
In ∆ODG and ∆OCG,
OD = OC                    | Radi fo the same arc
DG = CG                       | Arcs of equal radii
OG = OG                                   | Common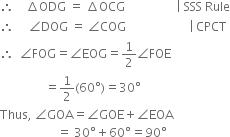

(iv) Join HJ and IJ

OI = OH                | Radii of the same arc
IJ = HJ                    | Arcs of equal radii
OJ=OJ                                | Common