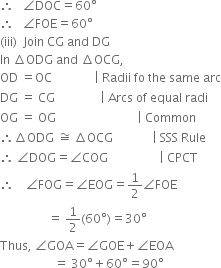Construct an angle of 90° at the initial point of a given ray and justify the construction.

Given: A ray OA.
Required: To construct an angle of 90° at O and justify the construction.
Steps of Construction:
1. Taking O as centre and some radius, draw an arc of a circle, which intersects OA, say at a point B.
2. Taking B as centre and with the same radius as before, draw an are intersecting the previously drawn are, say at a point C.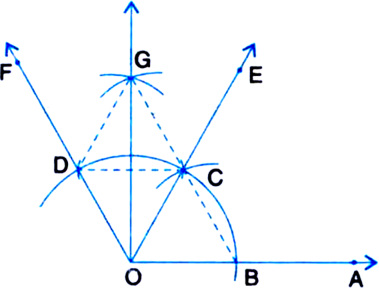

3. Taking C as centre and with the same radius as before, draw an arc intersecting the arc drawn in step 1, say at D.
4. Draw the ray OE passing through C. Then ∠EOA = 60°.
5. Draw the ray OF passing through D. Then ∠FOE = 60°.
6. Next, taking C and D as centres and with the radius more than  ID, draw arcs to intersect each other, say at G.

7. Draw the ray OG. This ray OG is the bisector of the angle ∠FOE, i.e., ∠FOG

Justification:
(i) Join BC.
Then. OC = OB = BC (By construction)
∴ ∆COB is an equilateral triangle.
∴ ∠COB = 60°.
∴ ∠EOA = 60°.
(ii) Join CD.
Then, OD = OC = CD (By construction)
∴ ∆DOC is an equilateral triangle.