Question
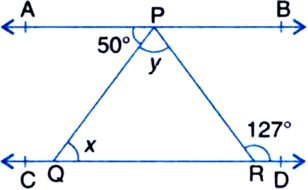
आकृति में, यदि PQ ⊥ PS और PQ||SR, ∠SQR = 28° और ∠QRT = 65° है, तो x और y के मान ज्ञात कीजिए।
Solution
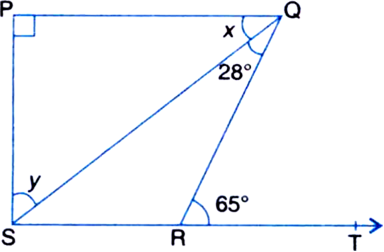
∠QRT = ∠RQS + ∠QSR
[ ∵बाह्य कोण प्रमेय ]
⇒ 65° = 28° + ∠QSR
⇒ ∠QSR = 65° - 28° = 37°
∵ PQ ≠ SP
∴ ∠QPS = 90°
∵ PQ || SR
∴ ∠QPS + ∠PSR = 180°
[ ∵ तिर्यक रेखा पर एक ही ओर बने कोण = 180° ]
⇒ 90° + ∠PSR = 180°
⇒ ∠PSR = 180° - 90° = 90°
⇒ ∠PSQ + ∠QSR = 90°
⇒ y + 37° = 90°
⇒ y = 90° - 37° = 53°
∆PQS में,
∠PQS + ∠QSP + ∠QPS = 180°
[ ∵ त्रिभुज के तीनों कोणों का योग = 180° ]
⇒ x + y + 90° = 180°
⇒ x + 53° + 90° = 180°
⇒ x + 143° = 180°
⇒ x = 180° - 143° = 37°
