Sponsor Area
Boolean Algebra
Derive a Canonical SOP expression for a Boolean function F, represented by the following truth table:
| U | V | W | F(U,V,W) |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
F(U,V,W)= U’V’W’ + U’VW’ + U’VW + UVW’
Some More Questions From Boolean Algebra Chapter
State DeMorgan’s Laws of Boolean Algebra and verify them using truth table.
Draw the Logic Circuit of the following Boolean Expression using only NOR Gates:
( A+B).(C+D)
( A+B).(C+D)
Derive a Canonical POS expression for a Boolean function G, represented by the following truth table:
X
Y
X
G(X,Y,Z)
0
0
0
0
0
0
1
0
0
1
0
1
0
1
1
0
1
0
0
1
1
0
1
1
1
1
0
0
1
1
1
1
Reduce the following Boolean expression to its simplest form using K-Map:
E(U,V,Z,W)= Σ (2,3,6,8,9,10,11,12,13)
E(U,V,Z,W)= Σ (2,3,6,8,9,10,11,12,13)
Verify the following using Boolean Laws.
A’+ B’.C = A’.B’.C’+ A’.B.C’+ A’.B.C + A’.B’.C+ A.B’.C
A’+ B’.C = A’.B’.C’+ A’.B.C’+ A’.B.C + A’.B’.C+ A.B’.C
Write the Boolean Expression for the result of the Logic Circuit as shown below:
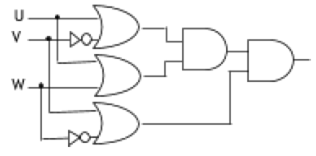

Derive a Canonical POS expression for a Boolean function F, represented by the following truth table:
P
Q
R
F(P, Q, R)
0
0
0
0
0
0
1
1
0
1
0
1
0
1
1
0
1
0
0
0
1
0
1
0
1
1
0
1
1
1
1
1
Reduce the following Boolean Expression to its simplest form using K-Map:
F(X,Y,Z,W)= (2,6,7,8,9,10,11,13,14,15)
F(X,Y,Z,W)= (2,6,7,8,9,10,11,13,14,15)
Verify the following using Boolean Laws.
X + Y' = X.Y+ X.Y'+ X'.Y'
X + Y' = X.Y+ X.Y'+ X'.Y'
Derive a Canonical SOP expression for a Boolean function F, represented by the following truth table :
A
B
C
F(A,B,C)
0
0
0
1
0
0
1
0
0
1
0
0
0
1
1
1
1
0
0
1
1
0
1
0
1
1
0
0
1
1
1
1
Sponsor Area
Mock Test Series
Mock Test Series





