Sponsor Area
Boolean Algebra
Verify the following using Boolean Laws.
A’+ B’.C = A’.B’.C’+ A’.B.C’+ A’.B.C + A’.B’.C+ A.B’.C
LHS
A’ + B’.C
= A’.(B + B’).(C + C’) + (A + A’).B’.C
= A’.B.C + A’.B.C’ + A’.B’.C + A’.B’.C’ + A.B’.C + A’.B’.C
= A’.B.C + A’.B.C’ + A’.B’.C + A’.B’.C’ + A.B’.C
= A’.B’.C’ + A’.B.C’ + A’.B.C + A’.B’.C + A.B’.C
= RHS
Some More Questions From Boolean Algebra Chapter
Verify the following using Boolean Laws.
A’+ B’.C = A’.B’.C’+ A’.B.C’+ A’.B.C + A’.B’.C+ A.B’.C
A’+ B’.C = A’.B’.C’+ A’.B.C’+ A’.B.C + A’.B’.C+ A.B’.C
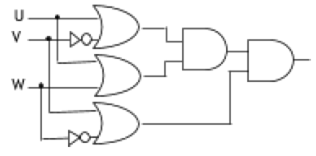
Write the Boolean Expression for the result of the Logic Circuit as shown below:

Derive a Canonical POS expression for a Boolean function F, represented by the following truth table:
P
Q
R
F(P, Q, R)
0
0
0
0
0
0
1
1
0
1
0
1
0
1
1
0
1
0
0
0
1
0
1
0
1
1
0
1
1
1
1
1
Reduce the following Boolean Expression to its simplest form using K-Map:
F(X,Y,Z,W)= (2,6,7,8,9,10,11,13,14,15)
F(X,Y,Z,W)= (2,6,7,8,9,10,11,13,14,15)
Verify the following using Boolean Laws.
X + Y' = X.Y+ X.Y'+ X'.Y'
X + Y' = X.Y+ X.Y'+ X'.Y'
Derive a Canonical SOP expression for a Boolean function F, represented by the following truth table :
A
B
C
F(A,B,C)
0
0
0
1
0
0
1
0
0
1
0
0
0
1
1
1
1
0
0
1
1
0
1
0
1
1
0
0
1
1
1
1
Draw the Logic Circuit for the following Boolean Expression :
(U + V').W' + Z
(U + V').W' + Z
Reduce the following Boolean Expression to its simplest form using Kâ€Map :
F(X,Y,Z,W) = ∑(0,1,6,8,9,l0,11,12,15)
F(X,Y,Z,W) = ∑(0,1,6,8,9,l0,11,12,15)
Sponsor Area
Mock Test Series
Mock Test Series





