Sponsor Area
Boolean Algebra
State DeMorgan’s Laws of Boolean Algebra and verify them using truth table.
(i) (A.B)'=A'+B'
(ii) (A+B)'=A'.B'
Truth Table Verification:
(I)
| A | B | A.B | (A.B )' | A' | B' | A' + B' |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
(II)
|
A |
B |
A+B |
(A+B )' |
A' |
B' |
A' . B' |
|
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
0 |
1 |
1 |
0 |
1 |
0 |
0 |
|
1 |
0 |
1 |
0 |
0 |
1 |
0 |
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
Some More Questions From Boolean Algebra Chapter
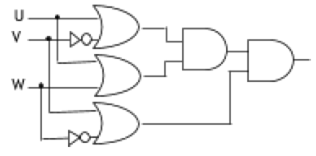
Write the Boolean Expression for the result of the Logic Circuit as shown below:

Derive a Canonical POS expression for a Boolean function F, represented by the following truth table:
P
Q
R
F(P, Q, R)
0
0
0
0
0
0
1
1
0
1
0
1
0
1
1
0
1
0
0
0
1
0
1
0
1
1
0
1
1
1
1
1
Reduce the following Boolean Expression to its simplest form using K-Map:
F(X,Y,Z,W)= (2,6,7,8,9,10,11,13,14,15)
F(X,Y,Z,W)= (2,6,7,8,9,10,11,13,14,15)
Verify the following using Boolean Laws.
X + Y' = X.Y+ X.Y'+ X'.Y'
X + Y' = X.Y+ X.Y'+ X'.Y'
Derive a Canonical SOP expression for a Boolean function F, represented by the following truth table :
A
B
C
F(A,B,C)
0
0
0
1
0
0
1
0
0
1
0
0
0
1
1
1
1
0
0
1
1
0
1
0
1
1
0
0
1
1
1
1
Draw the Logic Circuit for the following Boolean Expression :
(U + V').W' + Z
(U + V').W' + Z
Reduce the following Boolean Expression to its simplest form using Kâ€Map :
F(X,Y,Z,W) = ∑(0,1,6,8,9,l0,11,12,15)
F(X,Y,Z,W) = ∑(0,1,6,8,9,l0,11,12,15)
Sponsor Area
Mock Test Series
Mock Test Series





