Sponsor Area
TextBook Solutions for Uttarakhand Board Class 10 Mathematics Chapter 7 Coordinate Geometry
Question 1
If the distance between the points (4, k) and (1, 0) is 5, then what can be the possible values of k?
Solution
Let the points X (4,k) and Y(1,0)
It is given that the distance XY is 5 units.
By using the distance formula,
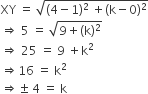
Sponsor Area
Sponsor Area
Mock Test Series
Mock Test Series