If a≠b≠0, prove that the points (a, a2), (b, b2) (0, 0) will not be collinear. - Wired Faculty

Coordinate Geometry

Question

If a≠b≠0, prove that the points (a, a2), (b, b2) (0, 0) will not be collinear.

Solution

Let A(a, a2), B(b, b2) and C(0, 0) be the coordinates of the given points.
We know that the area of a triangle having vertices (x₁, y₁), (x₂, y₂) and (x₃, y₃) is ∣∣12[x₁(y₂−y₃)+x₂(y₃−y₁)+x₃(y₁−y₂)]∣∣ square units.
So,
Area of ∆ABC\
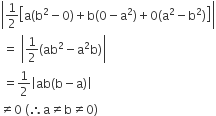
$open vertical bar 1 half open square brackets straight a left parenthesis straight b squared minus 0 right parenthesis plus straight b left parenthesis 0 minus straight a squared right parenthesis plus 0 left parenthesis straight a squared minus straight b squared right parenthesis close square brackets close vertical bar space equals space open vertical bar 1 half left parenthesis ab squared minus straight a squared straight b right parenthesis close vertical bar space equals 1 half open vertical bar ab left parenthesis straight b minus straight a right parenthesis close vertical bar not equal to 0 space left parenthesis therefore straight a not equal to straight b not equal to 0 right parenthesis$
Since the area of the triangle formed by the points (a, a²), (b, b²) and (0, 0) is not zero, so the given points are not collinear.

For Daily Free Study Material Join wiredfaculty

Coordinate Geometry

If a≠b≠0, prove that the points (a, a2), (b, b2) (0, 0) will not be collinear.

Some More Questions From Coordinate Geometry Chapter

Prove that the diagonals of a rectangle ABCD, with vertices A(2, -1), B(5, -1), C(5, 6) and D(2, 6), are equal and bisect each other.

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

Phone Number

Email Address

Loaction