Two charges 5 x 10–8C and –3 x 10–8 C are located 16 cm apart. At what point(s) on the line joining the two charges is the electric potential zero? Take the potential at infinity to be zero.
Charge, q1=
Charge, q2=–3 x 10–8 C
Distance between the two charges, d= 16 cm
The possibility of point where total potential due to q1 and q2 is zero may be that point which lies out side the segment joining q1 and q2.
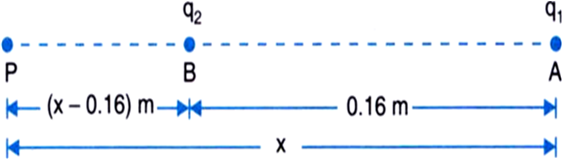
Let required point P lies 'x' distance away from and (x-0.16) distance away from q2 so that .
where, V1 is the potential at point P due to charge q1 and,
V2 is the potential at point P due to charge q2.
Now, using the forlmula for electrostatic potential at a given point we get,
That is, the required point is 40 cm away from q1 and (40 – 16) = 24 cm from q2 such that, potential is 0.





