Sponsor Area
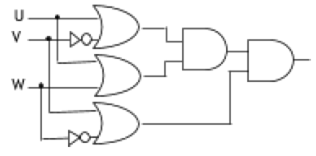
State Distributive Laws of Boolean Algebra and verify them using truth table.
(i) X. (Y+Z)= X.Y + X.Z
(ii) X + Y.Z= (X + Y). (X+Z)
(i)
| X | Y | Z | Y+Z | X.(Y+Z) | X.Y | X.Z | X.Y+X.Z |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| X | Y | Z | Y.Z | X+Y.Z | (X+Y) | (X+Z) | (X+Y).(X+Z) |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Derive a Canonical SOP expression for a Boolean function F, represented by the following truth table:
| U | V | W | F(U,V,W) |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
F(U,V,W)= U’V’W’ + U’VW’ + U’VW + UVW’
State DeMorgan’s Laws of Boolean Algebra and verify them using truth table.
(i) (A.B)'=A'+B'
(ii) (A+B)'=A'.B'
Truth Table Verification:
(I)
| A | B | A.B | (A.B )' | A' | B' | A' + B' |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
(II)
|
A |
B |
A+B |
(A+B )' |
A' |
B' |
A' . B' |
|
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
0 |
1 |
1 |
0 |
1 |
0 |
0 |
|
1 |
0 |
1 |
0 |
0 |
1 |
0 |
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
Derive a Canonical POS expression for a Boolean function G, represented by the following truth table:
| X | Y | X | G(X,Y,Z) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
G(X,Y,Z)= (X+Y+Z).( X+Y+Z’).( X+Y’+Z’).(X’+Y’+Z)
Verify the following using Boolean Laws.
A’+ B’.C = A’.B’.C’+ A’.B.C’+ A’.B.C + A’.B’.C+ A.B’.C
LHS
A’ + B’.C
= A’.(B + B’).(C + C’) + (A + A’).B’.C
= A’.B.C + A’.B.C’ + A’.B’.C + A’.B’.C’ + A.B’.C + A’.B’.C
= A’.B.C + A’.B.C’ + A’.B’.C + A’.B’.C’ + A.B’.C
= A’.B’.C’ + A’.B.C’ + A’.B.C + A’.B’.C + A.B’.C
= RHS
Write the Boolean Expression for the result of the Logic Circuit as shown below:
(U + V’).(U + W). (V + W’)
Derive a Canonical POS expression for a Boolean function F, represented by the following truth table:
| P | Q | R | F(P, Q, R) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
F(P,Q,R)=(P+Q+R).(P+Q’+R’).(P’+Q+R).(P’+Q+R’)
Reduce the following Boolean Expression to its simplest form using K-Map:
F(X,Y,Z,W)= (2,6,7,8,9,10,11,13,14,15)
F(X,Y,Z,W) = XY’ + ZW’ + XW + YZ
Verify the following using Boolean Laws.
X + Y' = X.Y+ X.Y'+ X'.Y'
L.H.S
=X + Y'
=X.(Y+Y')+ (X + X').Y'
=X.Y + X.Y' + X.Y' +X'.Y'
=X.Y + X.Y' + X'.Y'
=R.H.S
Derive a Canonical SOP expression for a Boolean function F, represented by the following truth table :
| A | B | C | F(A,B,C) |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
F(A,B,C) = A’B’C’ + A’BC + AB’C’ + ABC
Sponsor Area
Sponsor Area
