Sponsor Area
Let C be the circle with centre at(1,1) and radius 1. If T is the circle centred at (0,y) passing through origin and touching the circle externally, then the radius of T is equal to
1/2
1/4
D.
1/4
Let the coordinate of the centre of T be (0, K)
Distance between their centre
So, the radius of circle T is k i.e, 1/4
The image of line 
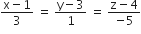in the plane 2x-y+z+3 =0 is the line
A.
Here, plane and line are parallel to each other. Equation of normal to the plane through the point (1,3,4) is
Any point in this normal is (2jk+2, -k+3,4+k)
Then, 
lies on the plane.
hence, point through which this image pass is
(2k+1,3-k,4+k)
i.e., (2(-2) + 1, 3+2, 4-2) = (-3,5,2)
Hence equation of image line is
A ray of light along 
get reflected upon reaching X -axis, the equation of the reflected ray is
B.
Given equation of line
Slope of incident ray is 
So, slope of reflected ray must be 
and the point of incident 
So equation of reflected ray
The number of values of k, for which the system of equations
(k+1) x + 8y = 4k
kx + (k+3)y = 3k -1
has no solution, is
infinite
1
2
3
B.
1
Condition for the system of equations has no solution,
Therefore, k = 3
Hence, only one value of k exists.
In a ∆PQR, if 3 sin P + 4 cos Q = 6 and 4 sin Q + 3 cos P = 1, then the angle R is equal to
5π/6
π/6
π/4
3π/4
B.
π/6
3 sin P + 4 cos Q = 6 ...... (1)
4 sin Q + 3 cos P = 1 ...... (2)
From (1) and (2) ∠P is obtuse.
(3 sin P + 4 cos Q)2+ (4 sin Q + 3 cos P)2= 37
⇒9 + 16 + 24 (sin P cos Q + cos P sin Q) = 37
⇒ 24 sin (P + Q) = 12
An equation of a plane parallel to the plane x – 2y + 2z – 5 = 0 and at a unit distance from the origin is
x – 2y + 2z – 3 = 0
x – 2y + 2z + 1 = 0
x – 2y + 2z – 1 = 0
x – 2y + 2z + 5 = 0
A.
x – 2y + 2z – 3 = 0
Perpendicular distance of the plane ax +by + cz +d =0 from the point
(x,y,z) is d =
Equation of plane parallel to x – 2y + 2z – 5 = 0 is x – 2y + 2z + k = 0 ...... (1)
perpendicular distance from O(0, 0, 0) to (1) is 1
If the line 2x + y = k passes through the point which divides the line segment joining the points (1, 1) and (2, 4) in the ratio 3 : 2, then k equals
29/5
5
6
11/5
C.
6
Line L : 2x +y = k passes through the point (say P) which divides a lie segment (say AB) in ratio 3:2 where A (1,1) and B (2,4).
Using section formula, the coordinates of the point P which divides AB internally in the ratio 3:2 are
Also, since the line L passes through P, hence substituting the coordinates of 
in the equation of line L: 2x +y = k,
we get
If the line 
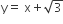
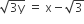
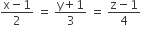and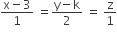 
intersect, then k is equal to
-1
2/9
9/2
0
C.
9/2
To find value of 'k' of the given lines L1 and L2 are intersecting each other.
Let 
⇒ Any point P on line L1 is of type
P(2p+1), 3p-1, 4p+1) and any point Q on line L2 is of type Q (q+3, 2q+k, q).
Since, L1 and L2 are intersecting each other, hence, both points P and Q should coincide at the point of intersection, i.e, corresponding coordinates of P and Q should be same.
2p+1 =q +3,
3p-1 =2q +k
4p+1 = q
solving these we get value of p and q as
p = -3/2 and q = -5
Substituting the values of p and q in the third equation
3p-1 = 2q+k, we get
Three numbers are chosen at random without replacement from {1, 2, 3, ...... 8}. The probability that their minimum is 3, given that their maximum is 6, is
3/8
1/5
1/4
2/5
B.
1/5
Let A be the event that maximum is 6.
B be event that minimum is 3
Required probability is 
A line is drawn through the point (1, 2) to meet the coordinate axes at P and Q such that it forms a triangle OPQ, where O is the origin. If the area of the triangle OPQ is least, then the slope of the line PQ is
-1/4
-4
-2
-1/2
C.
-2
The slope of line PQ 
Let 'm' be the slope of the line PQ, then the equation of PQ is
y -2 = m (x-1)
Now, PQ meets X-axis at P 
and y-axis at Q (0,2-m)
⇒ 
Now, f'(m) = 0
m = ± 2
f(2) =0
f(-2) = 8
Since, the area cannot be zero, hence the required value of m is -2
Sponsor Area
Sponsor Area
