Question
The number of values of k, for which the system of equations
(k+1) x + 8y = 4k
kx + (k+3)y = 3k -1
has no solution, is
-
infinite
-
1
-
2
-
3
Solution
B.
1
Condition for the system of equations has no solution,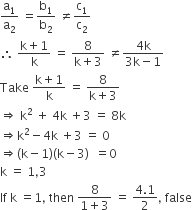
Therefore, k = 3
Hence, only one value of k exists.





