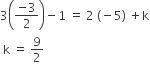Question
If the line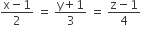 
and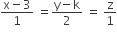 
intersect, then k is equal to
-
-1
-
2/9
-
9/2
-
0
Solution
C.
9/2
To find value of 'k' of the given lines L1 and L2 are intersecting each other.
Let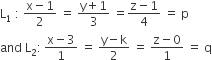 
⇒ Any point P on line L1 is of type
P(2p+1), 3p-1, 4p+1) and any point Q on line L2 is of type Q (q+3, 2q+k, q).
Since, L1 and L2 are intersecting each other, hence, both points P and Q should coincide at the point of intersection, i.e, corresponding coordinates of P and Q should be same.
2p+1 =q +3,
3p-1 =2q +k
4p+1 = q
solving these we get value of p and q as
p = -3/2 and q = -5
Substituting the values of p and q in the third equation
3p-1 = 2q+k, we get
