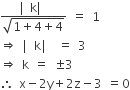Question
An equation of a plane parallel to the plane x – 2y + 2z – 5 = 0 and at a unit distance from the origin is
-
x – 2y + 2z – 3 = 0
-
x – 2y + 2z + 1 = 0
-
x – 2y + 2z – 1 = 0
-
x – 2y + 2z + 5 = 0
Solution
A.
x – 2y + 2z – 3 = 0
Perpendicular distance of the plane ax +by + cz +d =0 from the point
(x,y,z) is d =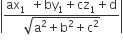
Equation of plane parallel to x – 2y + 2z – 5 = 0 is x – 2y + 2z + k = 0 ...... (1)
perpendicular distance from O(0, 0, 0) to (1) is 1
